三点共线习题 | 平面向量

前言

判断依据：

三点共线的应用类型：①判断是否三点共线；②已知三点共线，求参数的值；③三点不能构成三角形，求参数的值，即满足 \(\overrightarrow{AB}=k\overrightarrow{AC}\)；

典例剖析

【2024高一专项】已知 \(\overrightarrow{AB}=3(\vec{e_1}+\vec{e_2})\)，\(\overrightarrow{CB}=\vec{e_2}-\vec{e_1}\)，\(\overrightarrow{CD}=2\vec{e_1}+\vec{e_2}\)，则下列结论中成立的是 【\(\qquad\)】

$A.\quad A、B、C \textbf{三点共线}$ $B.\quad A、B、D \textbf{三点共线}$ $C.\quad A、D、C \textbf{三点共线}$ $D.\quad D、B、C \textbf{三点共线}$

解: \(\overrightarrow{AC}=\overrightarrow{AB}-\overrightarrow{CB}=3(\vec{e_1}+\vec{e_2})-(\vec{e_2}-\vec{e_1})=4\vec{e_1}+2\vec{e_2}=2\overrightarrow{CD}\)，

所以 \(A\)、\(D\)、 \(C\) 三点共线，故选: \(C\) .

解后反思：补充排除选项 \(A\)、\(B\)、\(D\)的思路方法。比如排除选项\(A\)的具体过程如下：

由于 \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=4\vec{e_1}+2\vec{e_2}\)，

假如 \(A\)、\(B\)、 \(C\) 三点共线，则存在唯一的实数 \(k\) ，使得 \(\overrightarrow{AB}=k\overrightarrow{AC}\)，

即 \(3(\vec{e_1}+\vec{e_2})=k(4\vec{e_1}+2\vec{e_2})\)，即 \((4k-3)\vec{e_1}=(3-2k)\vec{e_2}\)，

\(\left\{\begin{array}{l}{4k-3=0}\\{3-2k=0}\end{array}\right.\)， 此方程无解，

即不存在唯一的实数 \(k\) ，使得 \(\overrightarrow{AB}=k\overrightarrow{AC}\)，则 \(A\)、\(B\)、 \(C\) 三点不共线；

【2024高一专项】已知向量 \(\vec{a}\)，\(\vec{b}\) 不共线，\(\overrightarrow{OA}=\lambda\vec{a}+\mu\vec{b}\)，\(\overrightarrow{OB}=3\vec{a}-2\vec{b}\)，\(\overrightarrow{OC}=2\vec{a}+3\vec{b}\)，若 \(A\)、\(B\)、\(C\) 三点共线，则实数 \(\lambda\)， \(\mu\) 满足【\(\qquad\)】

$A.\lambda=\mu-1$ $B.\lambda=\mu+5$ $C.\lambda=5-\mu$ $D.\mu=13-5 \lambda$

思路1： \(\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=(\lambda\vec{a}+\mu\vec{b})-(3\vec{a}-2\vec{b})=(\lambda-3)\vec{a}+(\mu+2)\vec{b}\) ，

\(\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=2\vec{a}+3\vec{b}-(3\vec{a}-2\vec{b})=-\vec{a}+5\vec{b}\),

因为\(A\)、\(B\)、\(C\) 三点共线，所以 \(\overrightarrow{BA}//\overrightarrow{BC}\)，

必存在唯一的实数 \(k\) ，使得 \(\overrightarrow{BA}=k\overrightarrow{BC}\)，

由对应系数成比例可知，故 \(\cfrac{\lambda-3}{-1}=\cfrac{\mu+2}{5}\)，

即 \(-5(\lambda-3)=\mu+2\)，也即 \(\mu=13-5\lambda\)，故选: \(D\) .

思路2：利用【已知\(\overrightarrow{OC}=\lambda \overrightarrow{OA}+\mu \overrightarrow{OB}\)，其中\(\lambda+\mu=1\)，则 \(A、B、C\)三点共线】

由题可知， \(A\)、\(B\)、\(C\) 三点共线，则必存在唯一的实数 \(k\)，使得 \(\overrightarrow{OA}=k\cdot\overrightarrow{OB}+(1-k)\overrightarrow{OC}\)，

即 \(\lambda\vec{a}+\mu\vec{b}=(k+2)\vec{a}+(3-5k)\vec{b}\)，即 \((k+2-\lambda)\vec{a}=(\mu+5k-3)\vec{b}\)

则有 \(\left\{\begin{array}{l}{k+2-\lambda=0}\\{\mu+5k-3=0}\end{array}\right.\)， 解得 \(k=\lambda-2\)，

代入得到， \(\mu=13-5\lambda\)，故选: \(D\) .

【2024高一专项】设 \(\vec{e}_1\)， \(\vec{e}_2\) 是平面内两个不共线的向量， \(\overrightarrow{AB}=(a-1)\vec{e}_1+\vec{e}_2\)，\(\overrightarrow{AC}=2b\vec{e}_1-\vec{e}_2\)，\(a>0\)，\(b>0\)，若 \(A\)、\(B\)、\(C\) 三点共线，则 \(\cfrac{2}{a}\)\(+\)\(\cfrac{1}{b}\) 的最小值是 【\(\qquad\)】

$A.8$ $B.6$ $C.4$ $D.2$

简解：仿照上例，由 \(A\)、\(B\)、\(C\) 三点共线，所以向量 \(\overrightarrow{AB}\) 、\(\overrightarrow{A C}\) 共线，

通过计算能得到，\(a+2b=1\)，接下来题目就变成在限定条件下的最值求解了

则 \(\cfrac{2}{a}\)\(+\)\(\cfrac{1}{b}=(\cfrac{2}{a}+\cfrac{1}{b})(a+2b)=4+\cfrac{4b}{a}+\cfrac{a}{b}\)

\(\geqslant 4+2\sqrt{4}=8\)，当且仅当 \(a=\cfrac{1}{2}\)、\(b=\cfrac{1}{4}\) 时取到等号。 故选 \(A\) .

【2024高一专项】已知向量 \(\vec{e_1}\)，\(\vec{e_2}\) 不共线，且向量 \(\lambda\vec{e_1}+3\vec{e_2}\) 与 \(2\vec{e_1}-5\vec{e_2}\) 平行，则实数 \(\lambda\) 的值为【\(\qquad\)】

$A.-\cfrac{3}{5}$ $B.-\cfrac{6}{5}$ $C.-\cfrac{10}{3}$ $D.-4$

法1：利用平面向量共线基本定理求解，思路很严谨但速度慢，适合求解解答题；

由于向量 \(\vec{e_1}\)，\(\vec{e_2}\) 不共线，故向量 \(2\vec{e_1}-5\vec{e_2}\neq \vec{0}\)，否则若向量 \(2\vec{e_1}-5\vec{e_2}=\vec{0}\)，则 \(\vec{e_1}=\cfrac{5}{2}\vec{e_2}\)， 这说明向量 \(\vec{e_1}\)，\(\vec{e_2}\) 共线，与已知矛盾，故 \(2\vec{e_1}-5\vec{e_2}\neq \vec{0}\)。

又已知向量 \(\lambda\vec{e_1}+3\vec{e_2}\) 与 \(2\vec{e_1}-5\vec{e_2}\) 平行，则由平面向量共线定理可知，

必然存在唯一的实数 \(\mu\)，使得 \(\lambda\vec{e_1}+3\vec{e_2}\)\(=\mu\cdot\)\((2\vec{e_1}-5\vec{e_2})\)，

整理得到，\((2\mu-\lambda)\vec{e_1}=(3+5\mu)\vec{e_2}\)，

又由于向量 \(\vec{e_1}\)，\(\vec{e_2}\) 不共线，则 \(\vec{e_1}\neq\vec{0}\)，\(\vec{e_2}\neq\vec{0}\)，

故 \(\left\{\begin{array}{l}{2\mu-\lambda=0}\\{3+5\mu=0}\end{array}\right.\)， ^[1]

解得，\(\lambda=-\cfrac{6}{5}\) .

法2：利用对应系数成比例求解，思路不是很严谨但速度很快，适合求解选填题目；

已知向量 \(\lambda\vec{e_1}+3\vec{e_2}\) 与 \(2\vec{e_1}-5\vec{e_2}\) 平行，则由平面向量共线定理可知，

必然存在唯一的实数 \(\mu\)，使得 \(\lambda\vec{e_1}+3\vec{e_2}\)\(=\mu\cdot\)\((2\vec{e_1}-5\vec{e_2})\)，

即 \(\lambda\vec{e_1}+3\vec{e_2}\)\(=\)\(2\mu\vec{e_1}-5\mu\vec{e_2}\)，

则由对应系数成比例[对应系数相等包含在对应系数成比例中]可知，\(\cfrac{\lambda}{2\mu}=\cfrac{3}{-5\mu}\) ，

解得，\(\lambda=-\cfrac{6}{5}\) .

【2024高一专项】已知 \(\vec{a}\)， \(\vec{b}\) 是平面内两个不共线向量， \(\overrightarrow{AB}\)\(=\)\(m\vec{a}\)\(+\)\(2\vec{b}\)， \(\overrightarrow{BC}\)\(=\)\(3\vec{a}\)\(-\)\(\vec{b}\)，\(A\)、\(B\)、\(C\) 三点共线， 则实数 \(m=\)【\(\qquad\)】

$A.-\cfrac{2}{3}$ $B.\cfrac{2}{3}$ $C.-6$ $D.6$

解：因为 \(A\)、\(B\)、\(C\) 三点共线，

所以 \(\overrightarrow{AB}\)， \(\overrightarrow{BC}\) 共线， 又\(\vec{a}\)， \(\vec{b}\) 是平面内两个不共线向量，

所以可设 \(\overrightarrow{AB}=\lambda\overrightarrow{BC}\)， 因为 \(\overrightarrow{AB}\)\(=\)\(m\vec{a}\)\(+\)\(2\vec{b}\)， \(\overrightarrow{BC}\)\(=\)\(3\vec{a}\)\(-\)\(\vec{b}\)，

所以 \(m \vec{a}+2 \vec{b}=\lambda(3 \vec{a}-\vec{b})\),

所以 \(m=3\lambda\)， \(\lambda=-2\)，所以 \(m=-6\)，故选: \(C\) .

主动应用

• 这类题目往往没用明确告诉你三点共线，如果你能从题目中找的这个隐含条件，那么主动应用三点共线就可以灵活解题。有效挖掘题目中的隐含条件|高阶辅导

【主动应用三点共线解决问题】已知 \(\triangle OAB\) 中，延长 \(BA\) 到 \(C\)，使得 \(AB=AC\)，\(D\)是将 \(\overrightarrow{OB}\) 分成 \(2:1\) 的一个分点，\(DC\) 和 \(OA\) 交于点 \(E\)，设 \(\overrightarrow{OA}=\vec{a}\)， \(\overrightarrow{OB}=\vec{b}\)，

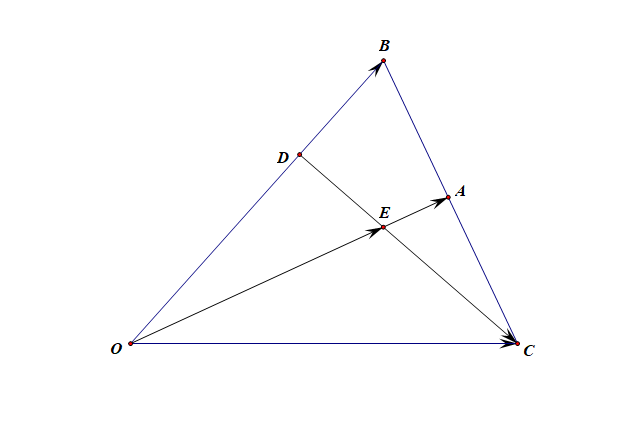
(1). 用 \(\vec{a}\) 和 \(\vec{b}\) 表示向量 \(\overrightarrow{OC}\) 和 \(\overrightarrow{DC}\) .

提示： \(\overrightarrow{OC}=2\vec{a}-\vec{b}\)， \(\overrightarrow{DC}=2\vec{a}-\cfrac{5}{3}\vec{b}\)，

(2). 若 \(\overrightarrow{OE}=\lambda\overrightarrow{OA}\)，求实数 \(\lambda\) 的值。

解：由于 \(\overrightarrow{OE}=\lambda\overrightarrow{OA}\)，

则 \(\overrightarrow{CE}=\overrightarrow{OE}-\overrightarrow{OC}=\lambda\overrightarrow{OA}-\overrightarrow{OC}\)，

\(=\lambda\vec{a}-2\vec{a}+\vec{b}=(\lambda-2)\vec{a}+\vec{b}\)，

又由图可知，\(C\)、\(D\)、\(E\) 三点共线，也即 \(\overrightarrow{CE}\) 与 \(\overrightarrow{CD}\) 共线，^[2]

则存在实数 \(m\) ，使得 \(\overrightarrow{CE}=m\overrightarrow{CD}\) ，

即 \((\lambda-2)\vec{a}+\vec{b}=m(-2\vec{a}+\cfrac{5}{3}\vec{b})\)，

即 \((\lambda+2m-2)\vec{a}=(\cfrac{5}{3}m-1)\vec{b}\)，

由于 \(\vec{a}\)、\(\vec{b}\) 不共线，故 \(\lambda+2m-2=\cfrac{5}{3}m-1=0\)，

解得 \(\lambda=\cfrac{4}{5}\) .

【人教 \(2019A\) 版教材\(P_{40}\) 页练习第 \(3\) 题】如图， 在 \(\triangle ABC\) 中， 点 \(O\) 是 \(BC\) 的中点， 过点 \(O\) 的直线分别交直线 \(AB\)， \(AC\) 于不同的两点 \(M\)，\(N\) .设 \(AB=mAM\)， \(AC=nAN\)， 求 \(m+n\) 的值.

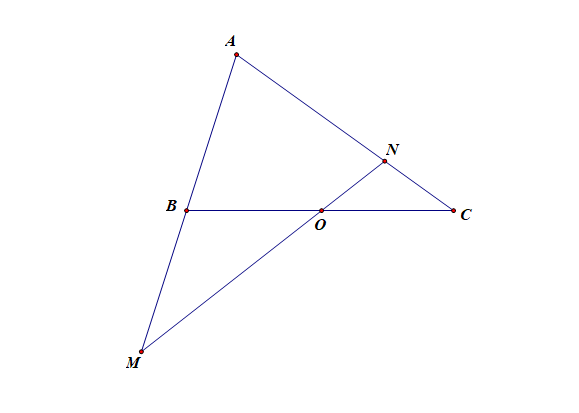
法1：取 \(\{\overrightarrow{AB}, \overrightarrow{AC}\}\) 为基底，令 \(\overrightarrow{AB}=\vec{a}\) ， \(\overrightarrow{AC}=\vec{b}\)， 则 \(\overrightarrow{AM}=\cfrac{1}{m}\vec{a}\)，\(\overrightarrow{AN}=\cfrac{1}{n}\vec{b}\) ，

由于 \(M\)，\(O\)， \(N\) 三点共线，故 \(\overrightarrow{MN}=\lambda\overrightarrow{MO}\)， 更多表达形式

即 \(\overrightarrow{AN}-\overrightarrow{AM}=\lambda(\overrightarrow{AO}-\overrightarrow{AM})\)，

则 \(\cfrac{1}{n}\vec{b}-\cfrac{1}{m}\vec{a}=\lambda(\cfrac{1}{2}\vec{a}+\cfrac{1}{2}\vec{b}-\cfrac{1}{m}\vec{a})\)

所以，\((\cfrac{\lambda}{2}-\cfrac{\lambda}{m}+\cfrac{1}{m})\vec{a}=(\cfrac{1}{n}-\cfrac{\lambda}{2})\vec{b}\)

由于 \(\vec{a}\)，\(\vec{b}\) 不共线，故 \(\left\{\begin{array}{l}{\cfrac{\lambda}{2}-\cfrac{\lambda}{m}+\cfrac{1}{m}=0}\\{\cfrac{1}{n}-\cfrac{\lambda}{2}=0}\end{array}\right.\quad\)

消去 \(\lambda\)，得到 \(m+n=2\) .

法2：取 \(\{\overrightarrow{AB}, \overrightarrow{AC}\}\) 为基底，令 \(\overrightarrow{AB}=\vec{a}\) ， \(\overrightarrow{AC}=\vec{b}\)， 则 \(\overrightarrow{AM}=\cfrac{1}{m}\vec{a}\)，\(\overrightarrow{AN}=\cfrac{1}{n}\vec{b}\) ，\(\overrightarrow{AO}=\cfrac{1}{2}\vec{a}+\cfrac{1}{2}\vec{b}\) ，

由于 \(M\)，\(O\)， \(N\) 三点共线，则必存在唯一实数 \(\lambda\) ，使得 \(\overrightarrow{AO}=\lambda\overrightarrow{AM}+(1-\lambda)\overrightarrow{AN}\)， 更多表达形式

即 \(\cfrac{1}{2}\vec{a}+\cfrac{1}{2}\vec{b}=\cfrac{\lambda}{m}\vec{a}+\cfrac{1-\lambda}{n}\vec{b}\)，

则 \((\cfrac{1}{2}-\cfrac{\lambda}{m})\vec{a}=(\cfrac{1-\lambda}{n}-\cfrac{1}{2})\vec{b}\)

由于 \(\vec{a}\)，\(\vec{b}\) 不共线，故 \(\left\{\begin{array}{l}{\cfrac{1}{2}-\cfrac{\lambda}{m}=0}\\{\cfrac{1-\lambda}{n}-\cfrac{1}{2}=0}\end{array}\right.\quad\)

消去 \(\lambda\)，得到 \(m+n=2\) .

思路汇总

【人教 \(2019A\) 版教材\(P_{32}\) 页例\(8\)题】已知点 \(A(-1,-1)\)，\(B(1,3)\)，\(C(2,5)\)，判断 \(A\)，\(B\)，\(C\) 三点之间的位置关系。

法1：初中的思路，利用距离公式 \(|AB|+|BC|=|AC|\) ，可以判断三点共线；

法2：利用向量方法 \(\overrightarrow{AB}=\lambda\overrightarrow{AC}\)，或用坐标运算来判断三点共线；

法3：利用向量方法 \(\overrightarrow{OA}=\lambda\overrightarrow{OB}+(1-\lambda)\overrightarrow{OC}\)，只要此时的参数 \(\lambda\) 的解存在即可，\(\lambda=3\)，

法4：利用斜率公式判断三点共线，\(k_{_{AB}}=k_{_{AC}}\) .

---

1. 否则，若 \(2\mu-\lambda\neq0\)，则 \(\vec{e_1}=\cfrac{3+5\mu}{2\mu-\lambda}\cdot\vec{e_2}\)，即说明向量 \(\vec{e_1}\)，\(\vec{e_2}\) 共线，与已知矛盾。 ↩︎

2. 题目已知 \(\overrightarrow{OE}=\lambda\overrightarrow{OA}\)，本来我们有了基底后，只要能将 \(\overrightarrow{OE}\) 和 \(\overrightarrow{OA}\) 用基底刻画，这样就能求得参数的关系或者参数的值，但是本题目的问题是没法将 \(\overrightarrow{OE}\) 用基底表达，所以我们还需要另外的关系式[当然此关系式需要包含有向量 \(\overrightarrow{OE}\)]，到时间将其替换为 \(\lambda\overrightarrow{OA}\)，而要找到关系等式，在向量中最好的莫过于共线的刻画了，也就是 \(C\)、\(E\)、\(D\) 三点共线，则有等式 \(\overrightarrow{CE}=m\overrightarrow{CD}\) ，这样就找到了关联两个式子的关键所在。 ↩︎