和差化积与积化和差|思维训练

前言

三角函数中的和差化积与积化合差公式是不需要记忆的，原来的教材中纯粹就没有这样的内容，现在的新教材将这一内容安排成了习题，主要是让学生进行思维训练。

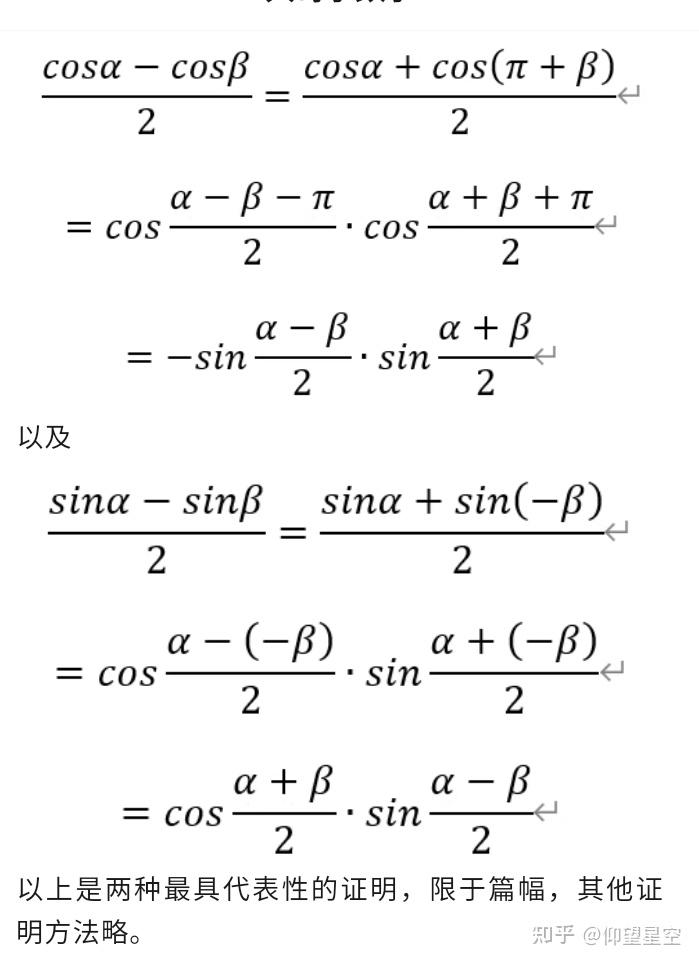
和差化积

\[\sin\alpha+\sin\beta=2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2} \]

\[\sin\alpha-\sin\beta=2\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2} \]

\[\cos\alpha+\cos\beta=2\cos\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2} \]

\[\cos\alpha-\cos\beta=-2\sin\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2} \]

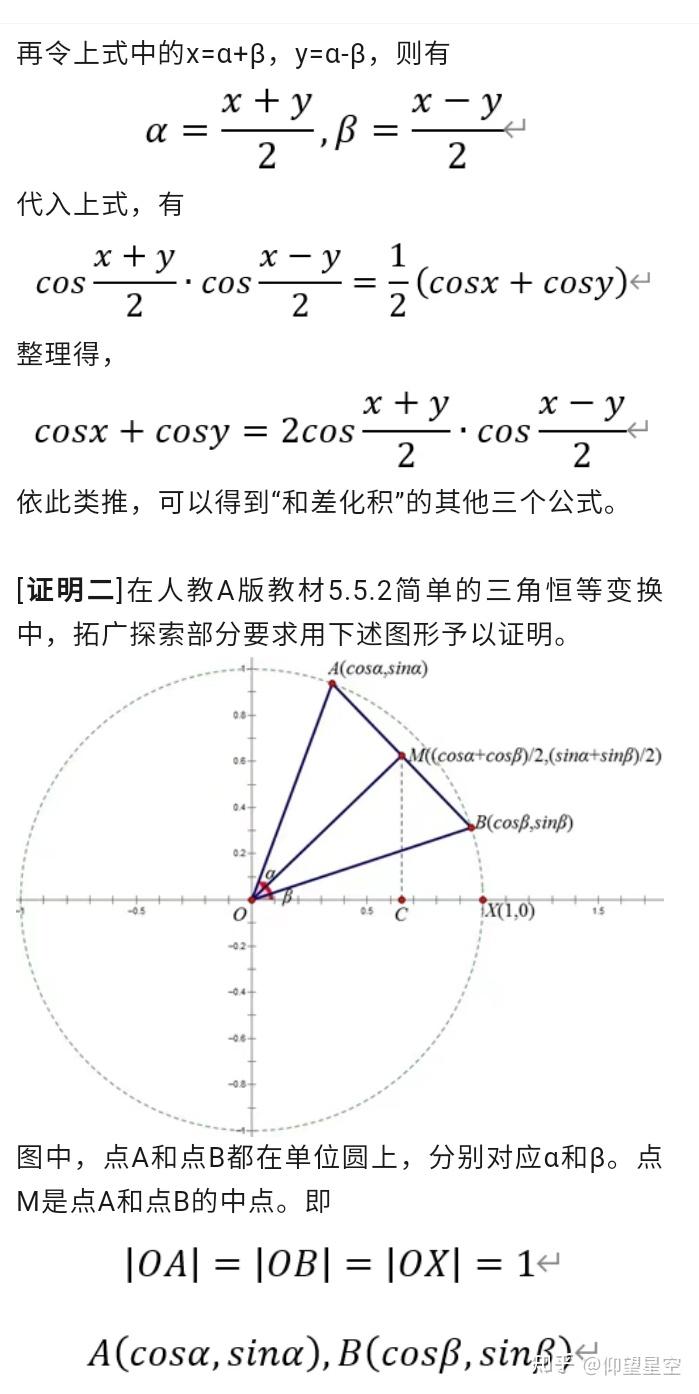
观察以上四个三角公式的结构，左边是两个三角函数的和与差的形式，而右边是两个三角函数的乘积的形式，故称之为和差化积公式。

积化和差

\[\sin A\cos B=\cfrac{1}{2}[\sin(A+B)+\sin(A-B)] \]

\[\cos A\sin B=\cfrac{1}{2}[\sin(A+B)-\sin(A-B)] \]

\[\cos A\cos B=\cfrac{1}{2}[\cos(A+B)+\cos(A-B)] \]

\[\sin A\sin B=-\cfrac{1}{2}[\cos(A+B)-\cos(A-B)] \]

观察以上四个三角公式的结构，左边是两个三角函数的乘积的形式，而右边是两个三角函数的和与差的形式，故称之为积化和差公式。

思维训练1

• 和差化积公式的证明

试证明：\(\sin\alpha+\sin\beta=2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)；

证明法1️⃣： 在三角函数的学习中，我们知道这样的公式：

\(\sin(A+B)=\sin A\cos B+\cos A\sin B\)；

\(\sin(A-B)=\sin A\cos B-\cos A\sin B\)；

则两式相加，得到

\(\sin(A+B)+\sin(A-B)=2\sin A\cos B①\)；

令\(A+B=\alpha\)，\(A-B=\beta\)，

则解方程可知：\(A=\cfrac{\alpha+\beta}{2}\)，\(B=\cfrac{\alpha-\beta}{2}\)，

将这一结果代入①式，就得到

\(\sin\alpha+\sin\beta=2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)；

解后反思1： ①式和要证明的式子的结构是一致的，故只需要换元就能完成证明，需要特别注意换元和反解的技巧。

证明法2️⃣： 我们已经知道如下的角的拆分技巧，更多请参阅三角函数中角的拆分与整合

$\alpha=\cfrac{(\alpha+\beta)+(\alpha-\beta)}{2}$，$\beta=\cfrac{(\alpha+\beta)-(\alpha-\beta)}{2}$，

还知道以下两角和的正弦公式：$$\sin(x+y)=\sin x\cos y+\cos x\sin y$$

将 \(\alpha\)，\(\beta\) 代入上述公式，则可知

$\sin\alpha$ $=$ $\sin\cfrac{(\alpha+\beta)+(\alpha-\beta)}{2}$ $=$ $\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}$ $+$ $\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2}①$

\(\sin\beta\) \(=\) \(\sin\cfrac{(\alpha+\beta)-(\alpha-\beta)}{2}\) \(=\) \(\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\) \(-\) \(\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2}②\)

①+②得到，\(\sin\alpha+\sin\beta=2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)，证毕 .

试证明：\(\sin\alpha+\sin\beta=2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)

证明：这个公式的由右向左证明思路如下所述：

\(2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)

\(=\)\(2\sin(\cfrac{\alpha}{2}+\cfrac{\beta}{2})\cos(\cfrac{\alpha}{2}-\cfrac{\beta}{2})\)

\(=2\left(\sin\cfrac{\alpha}{2}\cos\cfrac{\beta}{2}+\cos\cfrac{\alpha}{2}\sin\cfrac{\beta}{2}\right)\left(\cos\cfrac{\alpha}{2}\cos\cfrac{\beta}{2}+\sin\cfrac{\alpha}{2}\sin\cfrac{\beta}{2}\right)\)

\(=2\sin\cfrac{\alpha}{2}\cos\cfrac{\alpha}{2}\cos^2\cfrac{\beta}{2}+2\sin\cfrac{\beta}{2}\cos\cfrac{\beta}{2}\sin^2\cfrac{\alpha}{2}+2\sin\cfrac{\beta}{2}\cos\cfrac{\beta}{2}\cos^2\cfrac{\alpha}{2}+2\sin\cfrac{\alpha}{2}\cos\cfrac{\alpha}{2}\sin^2\cfrac{\beta}{2}\)

\(=\sin\alpha\cos^2\cfrac{\beta}{2}+\sin\beta\sin^2\cfrac{\alpha}{2}+\sin\beta\cos^2\cfrac{\alpha}{2}+\sin\alpha\sin^2\cfrac{\beta}{2}\)

\(=\sin\alpha(\cos^2\cfrac{\beta}{2}+\sin^2\cfrac{\beta}{2})+\sin\beta(\sin^2\cfrac{\alpha}{2}+\cos^2\cfrac{\alpha}{2})\)

\(=\sin\alpha+\sin\beta\)

〔解后反思2〕按照两角和差公式展开，整理即可得到结论，需要注意其中的运算。

试证明： \(\sin\alpha-\sin\beta=2\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2}\)；

证明：这个公式的由左向右的证明思路如下所述：

\(\sin\alpha-\sin\beta=\sin(\cfrac{\alpha+\beta}{2}+\cfrac{\alpha-\beta}{2})-\sin(\cfrac{\alpha+\beta}{2}-\cfrac{\alpha-\beta}{2})\)

\(=\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}+\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2}-\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}+\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2}\)

\(=2\cos\cfrac{\alpha+\beta}{2}\sin\cfrac{\alpha-\beta}{2}\)；

〔解后反思3〕注意角的拆分，比如 \(\alpha=\cfrac{\alpha+\beta}{2}+\cfrac{\alpha-\beta}{2}\)，\(\beta=\cfrac{\alpha+\beta}{2}-\cfrac{\alpha-\beta}{2}\)。

思维训练2

• 积化和差公式的证明

试证明：\(\sin A\cos B=\cfrac{1}{2}[\sin(A+B)+\sin(A-B)]\)；

证明： 由上述和差化积的结果可知：

\(\sin\alpha+\sin\beta=2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)；

如果我们对上述公式施行换元法的变换，

令\(\cfrac{\alpha+\beta}{2}=A\)，\(\cfrac{\alpha-\beta}{2}=B\)，

则\(A+B=\alpha\)，\(A-B=\beta\)，代入上述公式，得到

\(\sin(A+B)+\sin(A-B)=2\sin A\cos B\)；

对上述公式，移项整理即得到，

\(\sin A\cos B=\cfrac{1}{2}[\sin(A+B)+\sin(A-B)]\)；

试证明：\(\cos A\sin B=\cfrac{1}{2}[\sin(A+B)-\sin(A-B)]\)

试证明：\(\cos A\cos B=\cfrac{1}{2}[\cos(A+B)+\cos(A-B)]\)

对应练习1

仿照上述的解法，完成和差化积公式中的其他公式。

典例剖析

将函数 \(f(x)=\sin(4x+\cfrac{\pi}{3})+\sin(4x-\cfrac{\pi}{6})\) 化归为正弦型函数；

解法1：我们最容易想到的思路，打开整理结合辅助角公式，即

\(f(x)=\sin(4x+\cfrac{\pi}{3})+\sin(4x-\cfrac{\pi}{6})=\cfrac{\sqrt{3}+1}{2}\sin 4x+\cfrac{\sqrt{3}-1}{2}\cos 4x\)

到此，思维暂时受阻，\(\sqrt{(\cfrac{\sqrt{3}+1}{2})^2+(\cfrac{\sqrt{3}-1}{2})^2}=\sqrt{2}\)，\(\sin15^{\circ}=\sin\cfrac{\pi}{12}=\cfrac{\sqrt{6}-\sqrt{2}}{4}\)，

\(=\sqrt{2}(\sin4x\cdot\cfrac{\frac{\sqrt{3}+1}{2}}{\sqrt{2}}+\cos 4x\cdot\cfrac{\frac{\sqrt{3}-1}{2}}{\sqrt{2}})\)

\(=\sqrt{2}(\sin 4x\cfrac{\sqrt{6}+\sqrt{2}}{4}+\cos 4x\cfrac{\sqrt{6}-\sqrt{2}}{4})\)

\(=\sqrt{2}(\sin 4x\cos\cfrac{\pi}{12}+\cos 4x\sin\cfrac{\pi}{12})\)

\(=\sqrt{2}\sin(4x+\cfrac{\pi}{12})\)

解法2：使用和差化积公式\(\sin\alpha\)\(+\)\(\sin\beta\)\(=\)\(2\sin\cfrac{\alpha+\beta}{2}\cos\cfrac{\alpha-\beta}{2}\)，此时就能感受到和差化积公式的作用了，以此题为例，第二个因式中没有变量，只剩下角了。

\(f(x)=\sin(4x+\cfrac{\pi}{3})+\sin(4x-\cfrac{\pi}{6})\)

\(=2\sin\cfrac{(4x+\frac{\pi}{3})+(4x-\frac{\pi}{6})}{2}\cos\cfrac{(4x+\frac{\pi}{3})-(4x-\frac{\pi}{6})}{2}\)

\(=2\sin(4x+\cfrac{\pi}{12})\cos\cfrac{\pi}{4}\)

\(=\sqrt{2}\sin(4x+\cfrac{\pi}{12})\)

解法3：使用广义互余公式化简，我们使用比较多的广义互余公式是 \(\sin(\theta+\cfrac{\pi}{6})\)\(=\)\(\cos(\cfrac{\pi}{3}-\theta)\)，其中两个角中字母的系数互为相反数，如 \((\theta+\cfrac{\pi}{6})\)\(+\)\((\cfrac{\pi}{3}-\theta)\)\(=\)\(\cfrac{\pi}{2}\)，但实际考查中可能是两个角中字母的系数相同，此时它们的和不是 \(\cfrac{\pi}{2}\) ，但是其差\((\theta+\cfrac{\pi}{6})\)\(-\)\((\theta-\cfrac{\pi}{3})\)\(=\)\(\cfrac{\pi}{2}\)，比如实战中的 \(\sin(4x+\cfrac{\pi}{3})\)\(+\)\(\sin(4x-\cfrac{\pi}{6})\)，两个角 \((4x+\cfrac{\pi}{3})-(4x-\cfrac{\pi}{6})=\cfrac{\pi}{2}\)，此时只要利用关系 \(\sin(4x-\cfrac{\pi}{6})\)\(=\)\(-\cos(4x+\cfrac{\pi}{3})\)，也能简化运算，具体如下

\(f(x)=\sin(4x+\cfrac{\pi}{3})+\sin(4x-\cfrac{\pi}{6})\)

\(=\sin(4x+\cfrac{\pi}{3})+\sin(4x+\cfrac{\pi}{3}-\cfrac{\pi}{2})\)

\(=\sin(4x+\cfrac{\pi}{3})+\sin[(4x+\cfrac{\pi}{3})-\cfrac{\pi}{2}]\)

\(=\sin(4x+\cfrac{\pi}{3})-\cos(4x+\cfrac{\pi}{3})\)

\(=\sqrt{2}\left[\sin(4x+\cfrac{\pi}{3})\cdot\cfrac{\sqrt{2}}{2}-\cos(4x+\cfrac{\pi}{3})\cdot\cfrac{\sqrt{2}}{2}\right]\)

\(=\sqrt{2}\sin(4x+\cfrac{\pi}{12})\)