八卦图法

前言

本博文主要介绍八卦图法，能解决已知角 \(\theta\) 所在的象限，求分角 \(\cfrac{\theta}{n}\) 或倍角 \(n\cdot\theta\) 所在的象限。在后续的学习中，分角在三角函数的求值中使用较多，倍角使用的不多。

案例说明

已知 \(\theta\) 为第二象限角，则 \(\cfrac{\theta}{3}\) 为【\(\qquad\)】

$A$.第一或第二象限角

$B.$第一或第四象限角

$C.$第二或第四象限角

$D.$第一、第二或第四象限角

法1：不等式法，从数的角度求解；

解：用角度制来表达求解，关于对应的弧度制的求解，自己对照完成；

由于 \(\theta\) 为第二象限角，

所以 \(k\cdot360^{\circ}+90^{\circ}<\theta<k\cdot360^{\circ} +180^{\circ}，k\in Z\)

则 \(k\cdot120^{\circ}+30^{\circ}<\cfrac{\theta}{3}<k\cdot120^{\circ} +60^{\circ}，k\in Z\)

由于 \(k\in Z\)，故将所有的实数分以下三类分类讨论：

(1). 当 \(k=3n\)，\(n\in Z\) 时， 代入得到，

则 \(n\cdot360^{\circ}+30^{\circ}<\cfrac{\theta}{3}<n\cdot360^{\circ} +60^{\circ}，k\in Z\)

故此时角 \(\cfrac{\theta}{3}\) 为第一象限角；

(2). 当 \(k=3n+1\)，\(n\in Z\) 时， 代入得到，

则 \(n\cdot360^{\circ}+150^{\circ}<\cfrac{\theta}{3}<n\cdot360^{\circ} +180^{\circ}，k\in Z\)

故此时 角 \(\cfrac{\theta}{3}\) 为第二象限角；

(3). 当 \(k=3n+2\)，\(n\in Z\) 时， 代入得到，

则 \(n\cdot360^{\circ}+270^{\circ}<\cfrac{\theta}{3}<n\cdot360^{\circ} +300^{\circ}，k\in Z\)

故此时 角 \(\cfrac{\theta}{3}\) 为第四象限角；

综上所述， \(\cfrac{\theta}{3}\) 为第一、第二或第四象限角，故选 \(D\) .

法2：八卦图法，从形的角度求解；

解：由于求 \(\cfrac{\theta}{3}\)[压缩，需要将象限等分]，故将每一个象限都三等分，然后从 \(x\) 轴的正半轴开始按照逆时针方向标记Ⅰ、Ⅱ、Ⅲ、Ⅳ，一轮标记完成后再标记Ⅰ、Ⅱ、Ⅲ、Ⅳ，直到等分后的每一个部分被标记，又由于已知 \(\theta\) 为第二象限角，故最后寻找标记有 Ⅱ 的部分，如下图所示，我们发现，标记有 Ⅱ 的部分分别在第一、第二或第四象限，故\(\cfrac{\theta}{3}\) 为第一、第二或第四象限角，故选 \(D\) .

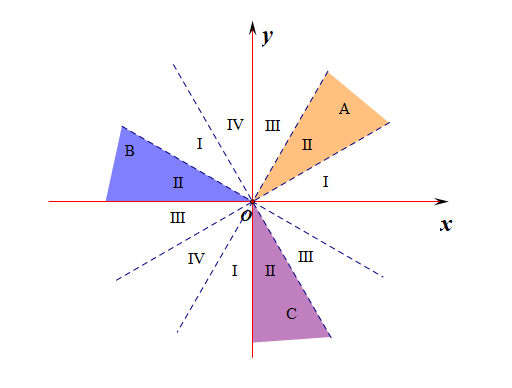
听完这个方法的同学都惊呼，为什么是这样，其实上面的已经完美的回答了这个问题，比如，当 \(k=3n\) 时对应图中的黄色区域 \(A\)；当 \(k=3n+1\) 时对应图中的蓝色区域 \(B\)；当 \(k=3n+2\) 时对应图中的紫色区域 \(C\)；正好体现了数与形的高度统一性。

已知 \(\theta\) 为第三象限角，则 \(2\theta\) 为第______________ 象限角

法1：不等式法，从数的角度求解；

解：用角度制来表达求解，关于对应的弧度制的求解，自己对照完成；

由于 \(\theta\) 为第三象限角，

所以 \(k\cdot360^{\circ}+180^{\circ}<\theta<k\cdot360^{\circ} +270^{\circ}，k\in Z\)

则 \(2k\cdot360^{\circ}+2\cdot 180^{\circ}<2\theta<2k\cdot360^{\circ} +2\cdot 270^{\circ}，k\in Z\)

即 \((2k+1)\cdot360^{\circ}+0^{\circ}<2\theta<(2k+1)\cdot360^{\circ} +180^{\circ}，k\in Z\)

故 \(2\theta\) 为第一或第二象限角或一二象限的象限界角。

法2：八卦图法，从形的角度求解；

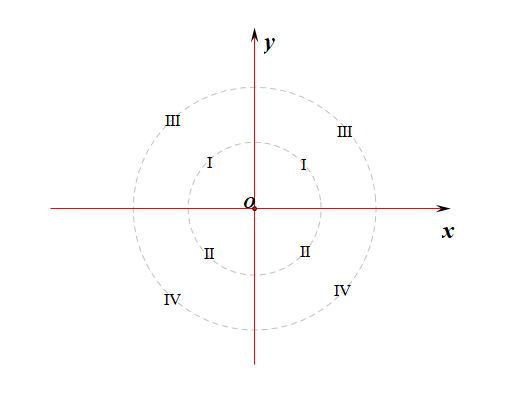
由于是求 \(2\theta\) [拉伸，需要将象限按倍数放大]，为便于标记完美，首先画两个同心圆，从 \(x\) 轴的正半轴开始按照逆时针方向标记，先在内圈标记，第一、二象限标记Ⅰ、Ⅰ，第三、四象限标记Ⅱ、Ⅱ，内圈标记完成；接下来再标记外圈，还是从 \(x\) 轴的正半轴开始按照逆时针方向标记，第一、二象限标记Ⅲ、Ⅲ，第三、四象限标记Ⅳ、Ⅳ，外圈标记完成[由于是2倍角，故只标记两圈]，故最后寻找标记有 Ⅲ 的部分，如下图所示，我们发现，标记有 Ⅲ 的部分分别在第一、第二象限或一二象限的象限界角，故\(2\theta\) 为第一、第二象限角或一二象限的象限界角。这个是不是体现了数与形的高度统一性呢，回答是肯定的。

典例剖析