主动引入参数 | 思维提升

前言

在数学题目的求解中，有时候需要我们主动引入参数，但当引入参数时，我们往往首先想到的是，我们人为的将题目的难度加大了，殊不知有时候恰当的引入参数可以大大简化题目的求解和证明，只是我们不习惯主动引入参数，担心引入后没法求得参数的值，从而走入了死胡同。其实这时候稍微了解和关联一些解方程理论，这一担心自然就会消弭于无形。当引入几个(\(n\) 个)参数时，我们只需要建立几个(\(n\) 个)独立的方程，就可以分别求得这几个(\(n\) 个)参数的值。

典例剖析

【引入一个参数，低阶层次】【2016全国卷Ⅲ】在\(\Delta ABC\)中，已知\(\angle B=\cfrac{\pi}{4}\)，\(BC\)边上的高等于\(\cfrac{1}{3}BC\)，则\(sinA\)=【\(\qquad\)】

$A、\cfrac{3}{10}$ $B、\cfrac{\sqrt{10}}{10}$ $C、\cfrac{\sqrt{5}}{5}$ $D、\cfrac{3\sqrt{10}}{10}$

分析：做出BC边的高线AD，由于注意到有了两个直角三角形，且\(\angle B=\cfrac{\pi}{4}\)，

则可以引入参数，设\(AD=x\)，则\(BD=x\)，\(AB=\sqrt{2}x\)，

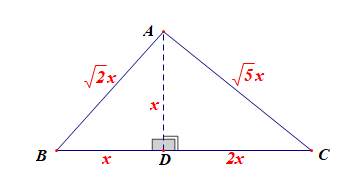
由题目可知\(BC=3x\)，则\(CD=3x-x=2x\) ，\(AC=\sqrt{5}x\)，

到此，在\(\Delta ABC\)中，三边都已经表示出来，且知道一个角，用正弦定理可得

\(\cfrac{\sqrt{5}x}{sin45^{\circ}}=\cfrac{3x}{sin\angle BAC}\)，化简得到\(sin\angle BAC=\cfrac{3\sqrt{10}}{10}\)，故选D

【解后反思】1、大胆引入参数，最后往往就会在运算中消失于无形；2、特别要注意特殊的直角三角形的边角关系，要熟记于心，以便于灵活运用。3、本题当然还可以先用余弦定理求得\(cosA\)，再求得\(sinA\)，但是走了弯路。

【引入两个参数，中阶层次】【2023高一暑假作业】已知 \(P\) 为 \(\triangle ABC\) 内一点， 且 \(3\overrightarrow{AP}\)\(+\)\(4\overrightarrow{BP}\)\(+\)\(5\overrightarrow{CP}\)\(=\)\(\overrightarrow{0}\)。 延长 \(AP\) 交 \(BC\) 于点 \(D\)， 若 \(\overrightarrow{AB}=\vec{a}\)， \(\overrightarrow{AC}=\vec{b}\)， 用 \(\vec{a}\) 、\(\vec{b}\) 表示向量 \(\overrightarrow{AP}\) 、 \(\overrightarrow{AD}\)。

分析：解读题目要求，我们能知道本题目考查的是向量的线性表示，是以向量 \(\vec{a}\) 、\(\vec{b}\) 作为平面向量族的基底线性表示向量 \(\overrightarrow{AP}\) ，我们只需要将已知条件中的其他的向量如 \(\overrightarrow{BP}\)、\(\overrightarrow{CP}\) 转化为用向量 \(\vec{a}\)、\(\vec{b}\) 和 \(\overrightarrow{AP}\) 表示，再加以整理即可。

解析: 由于 \(\overrightarrow{BP}=\overrightarrow{AP}-\overrightarrow{AB}=\overrightarrow{AP}-\vec{a}\)， \(\overrightarrow{CP}=\overrightarrow{AP}-\overrightarrow{AC}=\overrightarrow{AP}-\vec{b}\)，

又 \(3\overrightarrow{AP}+4\overrightarrow{BP}+5\overrightarrow{CP}=\vec{0}\)，\(3\overrightarrow{AP}+4(\overrightarrow{AP}-\vec{a})+5(\overrightarrow{AP}-\vec{b})=\vec{0}\)，

化简， 得 \(\overrightarrow{AP}=\cfrac{1}{3}\vec{a}+\cfrac{5}{12}\vec{b}\) 。

〔第二问的思路的探究，难点〕很显然，第二问也是考查向量的线性表示，但是此时的难点变成了主动引入参数。如果不引入参数，这样的线性表达就会转圈的回到原点，没法解答了。你们可以先试一试。

设 \(\overrightarrow{AD}=t\overrightarrow{AP}(t\in R)\)，则 \(\overrightarrow{AD}=\cfrac{1}{3}t\vec{a}+\cfrac{5}{12}t\vec{b}\). ①

再设 \(\overrightarrow{BD}=k\overrightarrow{BC}(k\in R)\)，

由 \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=\vec{b}-\vec{a}\)， 得 \(\overrightarrow{BD}=k(\vec{b}-\vec{a})\)。

而 \(\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\vec{a}+\overrightarrow{BD}\)，

故 \(\overrightarrow{AD}=\vec{a}+k(\vec{b}-\vec{a})=(1-k)\vec{a}+k\vec{b}\)， ②

由①②可知， 得 \(\left\{\begin{array}{l}\cfrac{1}{3}t=1-k\\ \cfrac{5}{12}t=k.\end{array}\right.\)

解得 \(t=\cfrac{4}{3}\)，代入①， 有 \(\overrightarrow{AD}=\cfrac{4}{9}\vec{a}+\cfrac{5}{9}\vec{b}\) 。

〔解后反思〕本题目为什么要引入参数，并且还要主动引入两个参数，这对我们的解题思维是个挑战，也是个提升。当经过尝试我们发现求而不得时，我们探求思路会发现，向量 \(\overrightarrow{AP}\) 和向量 \(\overrightarrow{AD}\) 共线，再结合第一问的结果，可能会想到 \(\overrightarrow{AD}=t\overrightarrow{AP}\)，这样就实现了将向量 \(\overrightarrow{AD}\)线性表示了，但此时只有一个方程，没法求得参数 \(t\) ，故还需要从另外的角度再将向量 \(\overrightarrow{AD}\)线性表示，则还需要再引入另外一个不同的参数比如 \(k\)，这样利用同一法，同一个向量的相同基底的线性表达的系数必然是相等的，就可以建立关于参数 \(t\) 和 \(k\) 的二元一次方程组，就可以求得参数 \(t\) 的值，从而本题目可解。

【引入三个参数，高阶层次】如图，平行四边形\(OACB\)中，\(BD=\cfrac{1}{3}BC\)，\(OD\)与\(AB\)相交于点\(E\)，求证：\(BE=\cfrac{1}{4}BA\)；

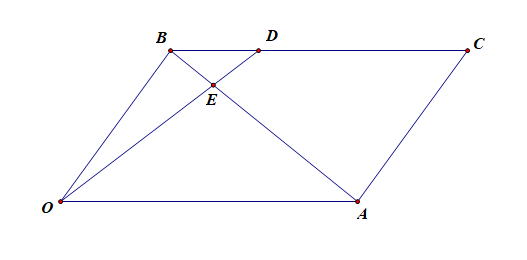
分析：借助向量知识，只须证明\(\overrightarrow{BE}=\cfrac{1}{4}\overrightarrow{BA}\)，而\(\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{BC}\)，又\(O、D、E\)三点共线，存在唯一实数对\(\lambda\)，\(\mu\)，且\(\lambda+\mu=1\)，使\(\overrightarrow{BE}=\lambda \overrightarrow{BO}+\mu \overrightarrow{BD}\)，从而得到\(\overrightarrow{BE}\)与\(\overrightarrow{BA}\)的关系。

证明：由已知条件，\(\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{BC}\)，又\(B、E、A\)三点共线，可设\(\overrightarrow{BE}=k\overrightarrow{BA}\)，

则\(\overrightarrow{BE}=k\overrightarrow{BO}+k\overrightarrow{BC}①\)，

又\(O、D、E\)三点共线，存在唯一实数对\(\lambda\)，\(\mu\)，且\(\lambda+\mu=1\)，使\(\overrightarrow{BE}=\lambda \overrightarrow{BO}+\mu \overrightarrow{BD}\)，

又\(\overrightarrow{BD}=\cfrac{1}{3}\overrightarrow{BC}\)，

则\(\overrightarrow{BE}=\lambda \overrightarrow{BO}+\cfrac{1}{3}\mu\overrightarrow{BD}②\)，

根据①②可得，

\(\left\{\begin{array}{l}{k=\lambda}\\{k=\cfrac{1}{3}\mu}\\{\lambda+\mu=1}\end{array}\right.\) 解得\(\left\{\begin{array}{l}{k=\cfrac{1}{4}}\\{\lambda=\cfrac{1}{4}}\\{\mu=\cfrac{3}{4}}\end{array}\right.\)

故\(\overrightarrow{BE}=\cfrac{1}{4}\overrightarrow{BA}\)，即\(BE=\cfrac{1}{4}BA\)；

解后反思：借助向量知识，充分运用三点共线的向量性质和同一法解决问题，巧妙、简洁。

【上例的引申对照题目】【高阶层次】如图，平行四边形 \(OACB\) 中，\(BE=\cfrac{1}{4}BA\)，延长 \(OE\) 与 \(BC\) 相交于点\(D\)，求证：\(BD=\cfrac{1}{3}BC\)；

分析：借助向量知识，只须证明\(\overrightarrow{BD}=\cfrac{1}{3}\overrightarrow{BC}\)，而\(\overrightarrow{BA}=\overrightarrow{BO}+\overrightarrow{BC}\)，又\(O、D、E\)三点共线，存在唯一实数对\(\lambda\)，\(\mu\)，且\(\lambda+\mu=1\)，使\(\overrightarrow{BE}=\lambda \overrightarrow{BO}+\mu \overrightarrow{BD}\)，从而得到\(\overrightarrow{BD}\)与\(\overrightarrow{BC}\)的关系。

证明：由已知条件，令 \(\overrightarrow{BD}=k\overrightarrow{BC}\)，即 \(\overrightarrow{BD}=k\overrightarrow{OA}\)，

又 \(O、D、E\) 三点共线，存在唯一实数对 \(\lambda\)，\(\mu\)，且 \(\lambda+\mu=1①\) ，使 $\overrightarrow{BE} $$=$$\lambda \overrightarrow{BO}$ \(+\) \(\mu \overrightarrow{BD}\)，

又 \(\overrightarrow{BE}=\cfrac{1}{4}\overrightarrow{BA}=\cfrac{1}{4}(\overrightarrow{BO}+\overrightarrow{OA})\)，

则 \(\lambda \overrightarrow{BO}\) \(+\) \(\mu \overrightarrow{BD}\) \(=\cfrac{1}{4}(\overrightarrow{BO}+\overrightarrow{OA})\)

也即 \(\lambda \overrightarrow{BO}\) \(+\) \(k\cdot\mu \overrightarrow{OA}\) \(=\cfrac{1}{4}(\overrightarrow{BO}+\overrightarrow{OA})\)

整理得到，\((\lambda-\cfrac{1}{4})\overrightarrow{BO}=(\cfrac{1}{4}-k\cdot\mu)\overrightarrow{OA}②\)，

由于 \(\overrightarrow{BO}\) 与 \(\overrightarrow{OA}\) 不共线，根据①②可得，

\(\left\{\begin{array}{l}{\lambda=\cfrac{1}{4}}\\{k\mu=\cfrac{1}{4}}\\{\lambda+\mu=1}\end{array}\right.\) 解得\(\left\{\begin{array}{l}{k=\cfrac{1}{3}}\\{\lambda=\cfrac{1}{4}}\\{\mu=\cfrac{3}{4}}\end{array}\right.\)

故\(\overrightarrow{BD}=\cfrac{1}{3}\overrightarrow{BC}\)，即\(BD=\cfrac{1}{3}BC\)；

解后反思：借助向量知识，充分运用三点共线的向量性质和同一法解决问题，巧妙、简洁。

〔二级结论〕如图，给定平行四边形\(OACB\)，

1️⃣：若 \(BD=\cfrac{1}{3}BC\)，\(OD\)与\(AB\)相交于点\(E\)，则有：\(BE=\cfrac{1}{4}BA\)；

2️⃣：若 \(BE=\cfrac{1}{4}BA\)，延长 \(OE\) 与 \(BC\) 相交于点\(D\)，则有：\(BD=\cfrac{1}{3}BC\)；

相关链接

• 同一法