正四棱锥

前言

正四棱锥：如图所示，四棱锥\(P-ABCD\)是正四棱锥，则底面 \(ABCD\) 是正方形，侧面[如 \(PAB\)、\(PBC\) ]为 \(4\) 个全等的等腰三角形且有公共顶点，顶点在底面的投影是底面的中心。顶点在底面的射影是正方形的中心。三角形的底边就是正方形的边。

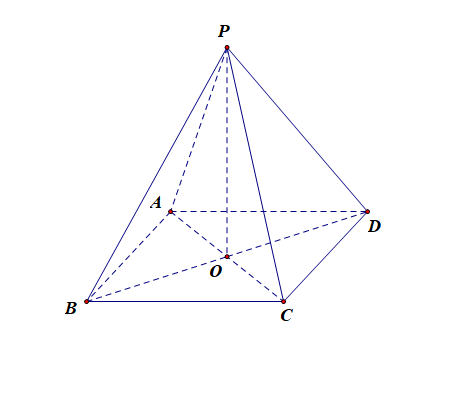
体积公式：\(V=\cfrac{1}{3}\times S\times h\)，\(S\) 为下底面正方形的面积， \(h=|PO|\) ；

表面积公式：\(S_{\text{表面积}}=4S_{\triangle PAB}+S_{\text{底}}\)， \(S_{\text{底}}=S_{\square ABCD}\)

侧面面积公式：\(S_{\text{侧}}=4S_{\triangle PAB}\)；

相关性质

(1). 正四棱锥各侧棱相等[ \(PA\)\(=\)\(PB\)\(=\)\(PC\)\(=\)\(PD\) ]，各侧面 [如 \(PAB\)、\(PBC\) ] 都是全等的等腰三角形，各等腰三角形底边 [如 \(BC\) ]上的高相等（它叫做正棱锥的斜高[如图中的 \(PE\) ]）；

(2). 正四棱锥的高[ \(PO\) ]、斜高[ \(PE\) ]和斜高在底面内的射影[ \(OE\) ]组成一个直角三角形[ \(Rt\triangle POE\) ]，正四棱锥的高[ \(PO\) ]、侧棱[ \(PC\) ]、侧棱在底面内的射影[ \(OC\) ]也组成一个直角三角形[ \(Rt\triangle POC\) ]；

(3). 正四棱锥的侧棱与底面所成的角[ \(\angle PCO\) ]都相等；正四棱锥的侧面与底面所成的二面角[ 其二面角对应的平面角为 \(\angle PEO\) ]都相等；

易混概念

正三棱锥：底面是正三角形，顶点在底面的射影是底面三角形的中心的三棱锥。(正三棱锥不等同于正四面体，正四面体必须每个面都是正三角形)。

典例剖析

【2022高三数学三轮模拟训练题】已知正四棱锥 \(P-ABCD\) 的顶点均在球 \(O\) 上，且该四棱锥的各个棱长均为 \(2\)， 则球 \(O\) 的表面积为【\(\qquad\)】

$A.4\pi$ $B.6\pi$ $C.8\pi$ $D.16\pi$

解析：设点 \(P\) 在底面 \(ABCD\) 的投影点为 \(O'\)，由于该四棱锥的各个棱长均为 \(2\)，\(PA\)\(=\)\(PB\)\(=\)\(PC\)\(=\)\(PD\)\(=\)\(AB\)\(=\)\(BC\)\(=\)\(CD\)\(=\)\(AD\)\(=\)\(2\)，^[1]，则 \(AO'=\cfrac{1}{2}AC=\sqrt{2}\) ，

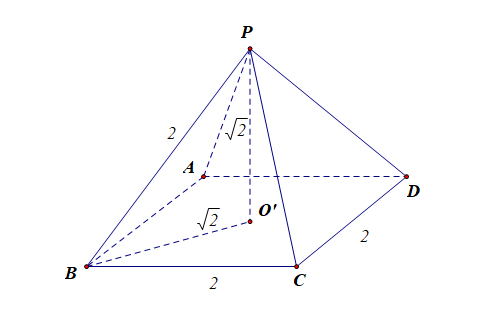
由题目可知，\(PO'\perp\) 平面 \(ABCD\) ，故 \(PO'=\sqrt{PA^2-AO'^2}=\sqrt{2}\) ，而底面 \(ABCD\) 所在截面圆的半径 \(AO'=\sqrt{2}\) ，故该截面圆即为过球心的圆，则 \(O'\) 是 正四棱锥 \(P-ABCD\) 的外接球的球心，则球的半径 \(R=\sqrt{2}\) ，故球 \(O\) 的表面积 \(S=4\pi R^2=8\pi\) ，故应该选 \(C\) 。

【2024高一质检二训练题】已知正四棱锥 \(S-ABCD\) 的底面边长和各侧棱长都为 \(2\)，点 \(S\)，\(A\)，\(B\)，\(C\)，\(D\) 都在同一球面上，则此球 \(O\) 的体积为____________ .

解析：借由上题可知，则球的半径 \(R=\sqrt{2}\) ，故球 \(O\) 的体积 \(V=\cfrac{4}{3}\pi R^3=\cfrac{8\sqrt{2}}{3}\pi\) .

探究总结

如上图所示，正四棱锥的外接球的球心 \(O'\) 一定在直线 \(PO\)上，如果点 \(O'\) 和点 \(O\)重合，则此时底面 \(ABCD\) 的外接圆为球体的最大圆。具体情况，可以参照下面的动态课件，自行探究总结。

---

1. 此处有个非常容易出错的地方，我们一般容易错误的认为棱锥的侧棱才叫棱，其实棱锥的各边都可以叫棱，即 \(AB\) 也可以叫棱，只不过它不能叫侧棱。再比如命题：棱柱的各条棱都相等。就是个假命题，原因是棱柱的底面的边也叫棱，但是不叫侧棱，所以棱柱的各条侧棱必然都相等，但是棱柱的各条棱不一定都相等，即底面的棱和侧棱不一定相等。 ↩︎