2021-2022学年高三文科数学讲座Ⅱ

思维导图

三角函数

典例剖析

化简：\(\sqrt{2+2cos8}+2\sqrt{1-sin8}\)

分析：如果你能注意到\(8=2\times 4\)，则可能想到利用二倍角公式，想办法将被开方数凑成一个完全平方数的形式，

原式\(=\sqrt{2}\sqrt{1+cos8}+2\sqrt{1-sin8}\)

\(=\sqrt{2}\sqrt{2cos^24}+2\sqrt{sin^24+cos^24-2sin4\cdot cos4}\)

\(=2|cos4|+2\sqrt{(sin4-cos4)^2}\)

\(=2|cos4|+2|sin4-cos4|\)

\(=-2cos4-2(sin4-cos4)=-2sin4\)

反思总结：\(4rad\approx 229^{\circ}\)，终边在第三象限的后半段，此时\(cos4>sin4\)。

化简\(\cfrac{(1+sin\theta+cos\theta)(sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})}{\sqrt{2+2cos\theta}}\)，其中\(0<\theta<\pi\)，

分析：原式\(=\cfrac{[(1+cos\theta)+sin\theta](sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})}{\sqrt{2(1+cos\theta)}}\)

\(=\cfrac{(2cos^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2})(sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})}{\sqrt{2\cdot 2cos^2\cfrac{\theta}{2}}}\)

\(=\cfrac{2cos\cfrac{\theta}{2}(cos\cfrac{\theta}{2}+sin\cfrac{\theta}{2})(sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})}{2cos\cfrac{\theta}{2}}\)

\(=sin^2\cfrac{\theta}{2}-cos^2\cfrac{\theta}{2}=-cos\theta\)。

【2020宝鸡市质检三文科第11题】著名数学家华罗庚先生被誉为“中国现代数学之父”，他倡导的“\(0.618\)优选法"在生产和科研实践中得到了非常广泛的应用，黄金分割比\(t=\cfrac{\sqrt{5}-1}{2}\approx 0.618\)，还可以表示成\(2\sin18^{\circ}\)，则\(\cfrac{2\cos^{2}27^{\circ}-1}{t\sqrt{4-t^{2}}}=\)【\(\qquad\)】

$A.4$ $B.\sqrt{5}-1$ $C.2$ $D.\cfrac{1}{2}$

分析：由于\(t=2\sin18^{\circ}\)，故有

\(\cfrac{2\cos^{2}27^{\circ}-1}{t\sqrt{4-t^{2}}}=\cfrac{\cos54^{\circ}}{2\sin18^{\circ}\sqrt{4-4\sin^{2}18^{\circ}}}=\cfrac{\cos54^{\circ}}{2\sin18^{\circ}\sqrt{4(1-\sin^{2}18^{\circ})}}\)

\(=\cfrac{\sin36^{\circ}}{2\sin18^{\circ}\cdot 2\cos18^{\circ}}=\cfrac{\sin36^{\circ}}{4\sin18^{\circ}\cos18^{\circ}}=\cfrac{1}{2}\)，故选\(D\).

在平面直角坐标系中，角 \(\alpha\) 的顶点在坐标原点，始边与 \(x\) 轴的非负半轴重合，若角 \(\alpha\) 的终边经过点 \(P\)\((\sin47^{\circ}\)\(,\)\(\cos47^{\circ})\) ，则 \(\sin(\alpha-13^{\circ})\)的值为【\(\qquad\)】

$A.\cfrac{1}{2}$ $B.\cfrac{\sqrt{3}}{2}$ $C.-\cfrac{1}{2}$ $D.-\cfrac{\sqrt{3}}{2}$

法1：利用三角函数的定义，令 \(P(x,y)\) ，则可知 \(x=\sin47^{\circ}\) ， \(y=\cos47^{\circ}\)，

则 \(r=|OP|=\sqrt{\sin^247^{\circ}+\cos^247^{\circ}}=1\)，

故 \(\sin\alpha=\cfrac{y}{r}=\cos47^{\circ}\) ， \(\cos\alpha=\cfrac{x}{r}=\sin47^{\circ}\) ，

则\(\sin(\alpha-13^{\circ})=\sin\alpha\cos13^{\circ}-\cos\alpha\sin13^{\circ}\)

\(=\cos47^{\circ}\cos13^{\circ}-\sin47^{\circ}\sin13^{\circ}\)

\(=\cos(47^{\circ}+13^{\circ})=\cos60^{\circ}=\cfrac{1}{2}\)，故选 \(A\).

法2：借助单位圆上点的坐标， 由于 \(\sin47^{\circ}=\cos43^{\circ}\)， \(\cos47^{\circ}=\sin43^{\circ}\)，

点 \(P\) 的坐标为 \((\cos43^{\circ},\sin43^{\circ})\) ，即 \(\alpha=43^{\circ}\)，

[或 \(\alpha=k\times 360^{\circ}+43^{\circ}\)，\(k\in Z\)，此处从简，取\(k=0\) ]

故 \(\sin(\alpha-13^{\circ})=\sin(43^{\circ}-13^{\circ})=\sin30^{\circ}=\cfrac{1}{2}\)，故选 \(A\).

【2020\(\cdot\)江西南昌调研】函数 \(y=\sin(\cfrac{x}{2}+\cfrac{\pi}{6})\) 的图像可以由函数 \(y=\cos\cfrac{x}{2}\) 的图像 【\(\quad\)】

$A.$向右平移$\cfrac{\pi}{3}$个单位长度得到

$B.$向右平移$\cfrac{2\pi}{3}$个单位长度得到

$C.$向左平移$\cfrac{\pi}{3}$个单位长度得到

$D.$向左平移$\cfrac{2\pi}{3}$个单位长度得到

解析 : 由 \(y=\cos\cfrac{x}{2}=\sin(\cfrac{x}{2}+\cfrac{\pi}{2})\)，

由于\(y=\sin[\cfrac{1}{2}(x-\cfrac{2\pi}{3})+\cfrac{\pi}{2}]=\sin(\cfrac{x}{2}+\cfrac{\pi}{6})\)，

可知函数 \(y=\sin(\cfrac{x}{2}+\cfrac{\pi}{6})\)的图像，

可以由 \(y=\cos\cfrac{x}{2}\)的图像向右平移\(\cfrac{2\pi}{3}\)个单位长度得到，故选\(B\).

难点反思：①为什么选\(y=\cos\cfrac{x}{2}=\sin(\cfrac{x}{2}+\cfrac{\pi}{2})\)这种变换？虽然\(y=\cos\cfrac{x}{2}=\sin(\cfrac{\pi}{2}-\cfrac{x}{2})\)，

但是若选取\(y=\sin(\cfrac{\pi}{2}-\cfrac{x}{2})\)开始变换，不仅需要横轴上的平移，还需要关于\(y\)轴的对称变换，故不采用后者；

②如本题目，我们做变换时，一般将函数名称统一，且将自变量的系数保持不变，这样就保证了只需要左右平移即可；

【2020 \(\cdot\) 湖北八校联考】已知 \(3\pi\leqslant\theta\leqslant 4\pi\)，且 \(\sqrt{\cfrac{1+\cos\theta}{2}}+\sqrt{\cfrac{1-\cos\theta}{2}}=\cfrac{\sqrt{6}}{2}\)， 则 \(\theta\)=【\(\quad\)】

$A.\cfrac{10\pi}{3}或\cfrac{11\pi}{3}$ $B.\cfrac{37\pi}{12}或\cfrac{47\pi}{12}$ $C.\cfrac{13\pi}{4}或\cfrac{15\pi}{4}$ $D.\cfrac{19\pi}{6}或\cfrac{23\pi}{6}$

解析：由于\(3\pi\leqslant\theta\leqslant 4\pi\)，则\(\cfrac{3\pi}{2}\leqslant \cfrac{\theta}{2}\leqslant 2\pi\)，所以\(\cos\cfrac{\theta}{2}>0\)，\(\sin \cfrac{\theta}{2}<0\)，

则\(\sqrt{\cfrac{1+\cos\theta}{2}}+\sqrt{\cfrac{1-\cos \theta}{2}}=\sqrt{\cos^{2}\cfrac{\theta}{2}}+\sqrt{\sin^{2}\cfrac{\theta}{2}}\)

\(=\cos \cfrac{\theta}{2}-\sin\cfrac{\theta}{2}=\sqrt{2}\cos(\cfrac{\theta}{2}+\cfrac{\pi}{4})=\cfrac{\sqrt{6}}{2}\)

则 \(\cos(\cfrac{\theta}{2}+\cfrac{\pi}{4})=\cfrac{\sqrt{3}}{2}\)，然后解三角方程即可；

即 \(\cfrac{\theta}{2}+\cfrac{\pi}{4}=\cfrac{\pi}{6}+2k\pi\) 或 \(\cfrac{\theta}{2}+\cfrac{\pi}{4}=-\cfrac{\pi}{6}+2k\pi\)， \(k\in Z\)

即 \(\theta=-\cfrac{\pi}{6}+4k\pi\) 或 \(\theta=-\cfrac{5\pi}{6}+4k\pi\)， \(k\in Z\)，

由于 \(3\pi\leqslant\theta\leqslant 4\pi\)， 故\(\theta=\cfrac{19\pi}{6}\) 或 \(\cfrac{23 \pi}{6}\)，故选\(D\).

已知\(\alpha，\beta\in (0，\pi)\)，且\(tan(\alpha-\beta)=\cfrac{1}{2}\)，\(tan\beta=-\cfrac{1}{7}\)，则\(2\alpha-\beta\)的值为________。

分析：由已知\(\alpha\in (0，\pi)\)，\(tan\alpha=tan[(\alpha-\beta)+\beta]=\cfrac{1}{3}>0\)，则\(\alpha\in (0，\cfrac{\pi}{2})\)，

又由于\(tan2\alpha=\cdots=\cfrac{3}{4}\)，则\(0<2\alpha<\cfrac{\pi}{2}\)，

又由于\(tan\beta=-\cfrac{1}{7}\)，\(\beta\in (0，\pi)\)，则\(\cfrac{\pi}{2}<\beta<\pi\)，

即\(tan(2\alpha-\beta)=\cdots=1\)，

又由于\(0<2\alpha<\cfrac{\pi}{2}\)，\(\cfrac{\pi}{2}<\beta<\pi\)，

则\(-\pi<2\alpha-\beta<0\)，故\(2\alpha-\beta=-\cfrac{3\pi}{4}\)；

【2017枣庄模拟】设\(\alpha\)为锐角，\(cos(\alpha+\cfrac{\pi}{6})=\cfrac{4}{5}\)，求\(sin(2\alpha+\cfrac{\pi}{12})\)的值；

分析：注意到已知角为一个\(\alpha+\cfrac{\pi}{6}\)，未知角也是一个\(2\alpha+\cfrac{\pi}{12}\)，

故二者之间的联系可能是从余、补、半、倍、特的角度建立联系，

故将已知角二倍得到\(2(\alpha+\cfrac{\pi}{6})=2\alpha+\cfrac{\pi}{3}\)，发现还是和未知角不一样，故做差就发现，

\[2\alpha+\cfrac{\pi}{12}=2(\alpha+\cfrac{\pi}{6})-\cfrac{\pi}{4} \]

故\(sin(2\alpha+\cfrac{\pi}{12})=sin[2(\alpha+\cfrac{\pi}{6})-\cfrac{\pi}{4}]\)

\(=sin[2(\alpha+\cfrac{\pi}{6})]cos\cfrac{\pi}{4}-cos[2(\alpha+\cfrac{\pi}{6})]sin\cfrac{\pi}{4}\)

\(=2sin(\alpha+\cfrac{\pi}{6})cos(\alpha+\cfrac{\pi}{6})cos\cfrac{\pi}{4}-[2cos^2(\alpha+\cfrac{\pi}{6})-1]sin\cfrac{\pi}{4}\)

\(=\cdots=\cfrac{17\sqrt{2}}{50}\).

• 备注：复杂一些的题目可能需要用到互余、互补、半角、倍角、特殊角中的某两个以上的角度才可以求解；

已知 \(\alpha\) 为锐角， \(\beta\) 为第二象限角，且 \(\cos(\alpha-\beta)=\cfrac{1}{2}, \sin(\alpha+\beta)=\cfrac{1}{2},\) 则 \(\sin(3\alpha-\beta)\)=【\(\quad\)】

$A.-\cfrac{1}{2}$ $B.\cfrac{1}{2}$ $C.\cfrac{\sqrt{3}}{2}$ $D.-\cfrac{\sqrt{3}}{2}$

法一: 因为 \(\alpha\) 为锐角， \(\beta\) 为第二象限角，

则有\(0<\alpha<\cfrac{\pi}{2}\)，\(2k\pi+\cfrac{\pi}{2}<\beta<2k\pi+\pi\)，\(k\in \Z\)，

故有\(2k\pi-\pi<\alpha-\beta<2k\pi\)，\(2k\pi+\cfrac{\pi}{2}<\alpha+\beta<2k\pi+\cfrac{3\pi}{2}\)，\(k\in \Z\)，

又由于\(\cos (\alpha-\beta)>0\)，\(\sin (\alpha+\beta)>0\)，

所以 \(\alpha-\beta\) 为第四象限角， \(\alpha+\beta\) 为第二象限角，

因此 \(\sin(\alpha-\beta)=-\cfrac{\sqrt{3}}{2}\)，\(\cos(\alpha+\beta)=-\cfrac{\sqrt{3}}{2}\)

所以 \(\sin2\alpha=\sin(\alpha-\beta+\alpha+\beta)=-\cfrac{\sqrt{3}}{2}\times(-\cfrac{\sqrt{3}}{2})+\cfrac{1}{2}\times\cfrac{1}{2}=1\)

因为 \(\alpha\) 为锐角，所以\(2\alpha=\cfrac{\pi}{2}\)，

所以 \(\sin(3\alpha-\beta)=\sin(2\alpha+\alpha-\beta)=\cos(\alpha-\beta)=\cfrac{1}{2}\)，选 \(B\).

法二: 因为 \(\alpha\) 为锐角， \(\beta\) 为第二象限角，

则有\(0<\alpha<\cfrac{\pi}{2}\)，\(2k\pi+\cfrac{\pi}{2}<\beta<2k\pi+\pi\)，\(k\in \Z\)，

故有\(2k\pi-\pi<\alpha-\beta<2k\pi\)，\(2k\pi+\cfrac{\pi}{2}<\alpha+\beta<2k\pi+\cfrac{3\pi}{2}\)，\(k\in \Z\)，

又由于\(\cos (\alpha-\beta)>0\)，\(\sin (\alpha+\beta)>0\)，

所以 \(\alpha-\beta\) 为第四象限角， \(\alpha+\beta\) 为第二象限角，

因此 \(\sin(\alpha-\beta)=-\cfrac{\sqrt{3}}{2}\)，\(\cos(\alpha+\beta)=-\cfrac{\sqrt{3}}{2}\)，

所以 \(\cos2(\alpha-\beta)=2\cos^{2}(\alpha-\beta)-1=2\times(\cfrac{1}{2})^{2}-1=-\cfrac{1}{2}\)，

\(\sin2(\alpha-\beta)=2\sin(\alpha-\beta)\cos(\alpha-\beta)=2\times(-\cfrac{\sqrt{3}}{2})\times\cfrac{1}{2}=-\cfrac{\sqrt{3}}{2}\)，

所以 \(\sin(3\alpha-\beta)=\sin[2(\alpha-\beta)+(\alpha+\beta)]\)

\(=\sin2(\alpha-\beta)\cos(\alpha+\beta)+\cos2(\alpha-\beta)\sin(\alpha+\beta)\)

\(=(-\cfrac{\sqrt{3}}{2})\times(-\cfrac{\sqrt{3}}{2})+(-\cfrac{1}{2})\times\cfrac{1}{2}=\cfrac{1}{2}\)，故选\(B\).

【2017\(\cdot\)全国卷Ⅲ】设函数 \(f(x)=\cos(x+\cfrac{\pi}{3})\)，则下列结论错误的是 【\(\qquad\)】

$A.f(x)$ 的一个周期为$2\pi$

$B.y=f(x)$的图象关于直线 $x=\frac{8\pi}{3}$对称

$C.f(x+\pi)$的一个零点为$x=\frac{\pi}{6}$

$D.f(x)$在$(\frac{\pi}{2}, \pi)$上单调递减

解析： \(f(x)\) 的最小正周期为 \(2\pi\)，易知 \(A\) 正确；

\(f(\cfrac{8\pi}{3})=\cos(\cfrac{8\pi}{3}+\cfrac{\pi}{3})=\cos3\pi=-1\)，为 \(f(x)\) 的最小值， 故 \(B\)正确；

因为 \(f(x+\pi)=\cos(x+\pi+\cfrac{\pi}{3})=-\cos(x+\cfrac{\pi}{3})\)，

所以\(f(\cfrac{\pi}{6}+\pi)=-\cos(\cfrac{\pi}{6}+\cfrac{\pi}{3})=-\cos\cfrac{\pi}{2}=0\)，故 \(C\)正确；

由\(f(\cfrac{2\pi}{3})=\cos(\cfrac{2\pi}{3}+\cfrac{\pi}{3})=-\cos\pi=-1\)，为 \(f(x)\) 的最小值，

故 \(f(x)\) 在 \((\cfrac{\pi}{2}, \pi)\) 上不单调，故\(D\)错误. 故选\(D\)；

【2019\(\cdot\)惠州模拟】将函数 \(f(x)=2\sin(2x+\phi)(\phi<0)\) 的图象向左平移 \(\cfrac{\pi}{3}\) 个单位长度，得到偶函数 \(g(x)\) 的图象，则 \(\phi\) 的最大值是_________.

解析: 依题设，\(g(x)=2\sin\left[2\left(x+\cfrac{\pi}{3}\right)+\phi\right]=2\sin\left(2x+\cfrac{2\pi}{3}+\phi\right)\)，

由\(g(x)\) 为偶函数，即\(x=0\)时，函数\(g(x)\)取得最值，即\(\cfrac{2\pi}{3}+\phi=k\pi+\cfrac{\pi}{2}\)， \(k\in Z\)，

所以 \(\phi=k\pi-\cfrac{\pi}{6}(k\in Z)\)，由于\(\phi<0\)，

故令\(k=0\)，得到\(\phi\) 的最大值为 \(-\cfrac{\pi}{6}\).

【2019·高考全国卷Ⅲ】设函数\(f(x)=\sin(\omega x+\cfrac{\pi}{5})\)\((\omega>0)\)，已知\(f(x)\)在\([0，2\pi]\)有且仅有\(5\)个零点。下述四个结论：

①\(f(x)\)在\((0，2\pi)\)有且仅有\(3\)个极大值点；

②\(f(x)\)在\((0，2\pi)\)有且仅有\(2\)个极小值点；

③\(f(x)\)在\((0，\cfrac{\pi}{10})\)上单调递增；

④\(\omega\) 的取值范围是\([\cfrac{12}{5}，\cfrac{29}{10})\)，

其中所有正确结论的编号是【\(\qquad\)】

$A.①④$ $B.②③$ $C.②③④$ $D.①③④$

解析：已知\(f(x)=\sin(\omega x+\cfrac{\pi}{5})(\omega>0)\) 在\([0, 2\pi]\) 有且仅有\(5\)个零点，如图，

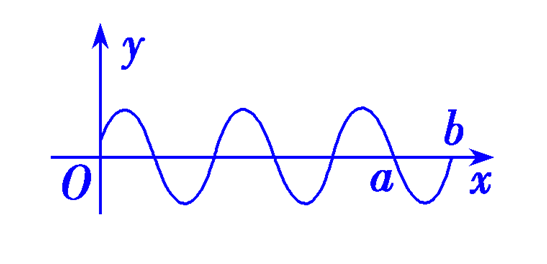
其图像的右端点的横坐标\(2\pi\) 在\([a, b)\)上时，此时 \(f(x)\) 在 \((0,2\pi)\) 有且仅有 \(3\)个极大值点，

但\(f(x)\)在\((0,2\pi)\)可能有\(2\)或\(3\)个极小值点，所以①正确，②不正确；

当\(x\in[0, 2\pi]\)时，\(\omega x+\cfrac{\pi}{5}\in[\cfrac{\pi}{5}, 2\pi\omega+\cfrac{\pi}{5}]\)，

由\(f(x)\) 在\([0,2\pi]\)有且仅有\(5\)个零点可得此处，当我们以\(\omega x+\cfrac{\pi}{5}\)为横轴做图像时，要保证有且仅有\(5\)个零点，必须限制右端点满足条件\(5\pi\leqslant 2\pi\omega+\cfrac{\pi}{5}<6\pi\)，\(5\pi\leqslant 2\pi\omega+\cfrac{\pi}{5}<6\pi\)

解得\(\omega\)的范围是\([\cfrac{12}{5},\cfrac{29}{10})\)，所以④正确；

当\(x\in (0,\cfrac{\pi}{10})\)时，\(\cfrac{\pi}{5}<\omega x+\cfrac{\pi}{5}<\cfrac{\pi\omega}{10}+\cfrac{\pi}{5}<\)\(\cfrac{49\pi}{100}<\cfrac{\pi}{2}\)，

[注释：由于\(\omega\in [\cfrac{12}{5},\cfrac{29}{10})\)，故\(\cfrac{\pi\omega}{10}+\cfrac{\pi}{5}<\cfrac{\pi}{10}\times \cfrac{29}{10}+\cfrac{\pi}{5}=\cfrac{49\pi}{100}\)]

所以 \(f(x)\) 在 \((0,\cfrac{\pi}{10})\) 单调递增，所以③正确. 故选\(D\).

【2019长沙模拟】已知\(P\)，\(Q\)是圆心在坐标原点\(O\)的圆上的两点，分别位于第一和第四象限，且点\(P\)的纵坐标为\(\cfrac{4}{5}\)，点\(Q\)的横坐标为\(\cfrac{5}{13}\)，则\(cos\angle POQ\)=___________.

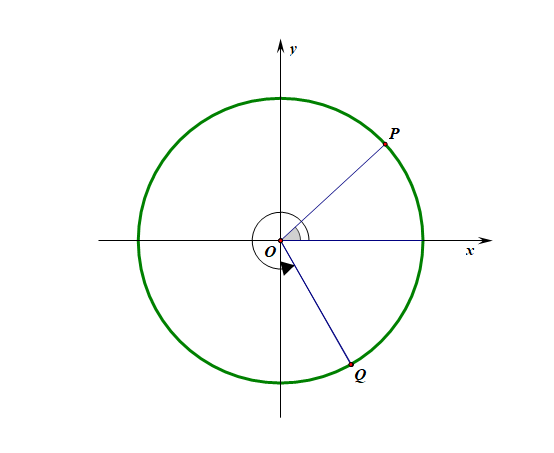
分析：由题可知，由于点\(P(\cfrac{3}{5}，\cfrac{4}{5})\)，则\(cos\angle xOP=\cfrac{3}{5}\)，\(sin\angle xOP=\cfrac{4}{5}\)，

又由于点\(Q(\cfrac{5}{13}，-\cfrac{12}{13})\)，\(cos\angle xOQ=\cfrac{5}{13}\)，\(sin\angle xOQ=-\cfrac{12}{13}\)，[注意，起始边为\(x\)轴非负半轴]

故\(\angle POQ\)即可以看成逆时针形成的正角\(\angle xOP\)和顺时针形成的负角\(\angle xOQ\)的差值\(\angle xOP-\angle xOQ\)，也可以看成逆时针形成的正角\(\angle xOQ\)和逆时针形成的正角\(\angle xOP\)的差值\(\angle xOQ-\angle xOP\)，最后计算\(cos\angle POQ\)的结果应该是一样的；

\(cos\angle POQ=cos(\angle xOP-\angle xOQ)=\cos\angle xOP\cdot\cos\angle xOQ+\sin\angle xOP\cdot\sin\angle xOQ\)

\(=\cfrac{3}{5}\times\cfrac{5}{13}+\cfrac{4}{5}\times(-\cfrac{12}{13})=-\cfrac{33}{65}\)

解后反思：本题目是高频易错题目，容易出现这样的错误，\(cos\angle POQ=cos(\angle xOP+\angle xOQ)=\cfrac{56}{65}\)

【2017高考真题 理科全国卷2的第14题】函数\(f(x)=sin^2x+\sqrt{3}cosx-\cfrac{3}{4}(x\in[0，\cfrac{\pi}{2}])\)的最大值为_______。

分析：由于\(x\in[0，\cfrac{\pi}{2}]\)，则\(cosx\in [0，1]\)， 令\(cosx=t\in [0，1]\)，

\(f(x)=1-cos^2x+\sqrt{3}cosx-\cfrac{3}{4}=1-t^2+\sqrt{3}t-\cfrac{3}{4}=-(t-\cfrac{\sqrt{3}}{2})^2+1=g(t)\)，

故当\(t=\cfrac{\sqrt{3}}{2}\)时，\(g(t)_{max}=f(x)_{max}=1\)。

反思总结：这类题目常有两个考查方向：①转化为正弦型求最值；②转化为二次型求最值。

已知函数\(f(x)=2sinx\cdot cosx+2\sqrt{3}\cdot cos^2x-\sqrt{3}+1\)，求解 ①求周期；②求值域；③求单调区间；④求对称性；

解析：\(f(x)=sin2x+\sqrt{3}(1+cos2x)-\sqrt{3}+1\)

\(=sin2x+\sqrt{3}cos2x+1\)

\(=2sin(2x+\cfrac{\pi}{3})+1\)

①求周期；由\(T=\cfrac{2\pi}{2}\)，得到\(T=\pi\)

②求值域\((x\in R 或 x\in [-\cfrac{\pi}{3}，\cfrac{\pi}{4}])\)；最值(和最值点)；

若\(x\in R\)，则

当\(sin(2x+\cfrac{\pi}{3})=1\)时，即\(2x+\cfrac{\pi}{3}=2k\pi+\cfrac{\pi}{2}(k\in Z)\)，即\(x=k\pi+\cfrac{\pi}{12}(k\in Z)\)时，\(f(x)_{max}=2\times1+1=3\)；

当\(sin(2x+\cfrac{\pi}{3})=-1\)时，即\(2x+\cfrac{\pi}{3}=2k\pi-\cfrac{\pi}{2}(k\in Z)\)，即\(x=k\pi-\cfrac{5\pi}{12}(k\in Z)\)时，\(f(x)_{max}=2\times(-1)+1=-1\)；

若\(x\in [-\cfrac{\pi}{3}，\cfrac{\pi}{4}]\)，则可得

\(-\cfrac{2\pi}{3}\leq 2x\leq \cfrac{\pi}{2}\)，则\(-\cfrac{\pi}{3}\leq 2x+\cfrac{\pi}{3}\leq \cfrac{5\pi}{6}\)，

故当\(2x+\cfrac{\pi}{3}=-\cfrac{\pi}{3}\)，即\(x=-\cfrac{\pi}{3}\)时，\(f(x)_{min}=f(-\cfrac{\pi}{3})=2\times (-\cfrac{\sqrt{3}}{2})+1=-\sqrt{3}+1\)；

故当\(2x+\cfrac{\pi}{3}=\cfrac{\pi}{2}\)，即\(x=\cfrac{\pi}{12}\)时，\(f(x)_{max}=f(\cfrac{\pi}{12})=2\times 1+1=3\)；

③求单调区间\(\left(x\in R 或x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{2}]\right)\)

在 \(R\) 上的单调递增区间为 \([k\pi-\cfrac{5\pi}{12},k\pi+\cfrac{\pi}{12}]\) \((k\in Z)\) ，单调递减区间为 \([k\pi+\cfrac{\pi}{12},k\pi+\cfrac{7\pi}{12}]\) \((k\in Z)\) ，

故在 \([-\cfrac{\pi}{4}，\cfrac{\pi}{2}]\) 上的单调递增区间 \([-\cfrac{\pi}{4}，\cfrac{\pi}{12}]\)，单调递减区间 \([\cfrac{\pi}{12}，\cfrac{\pi}{2}]\)；

④求函数\(f(x)\)对称轴方程和对称中心坐标；

令\(2x+\cfrac{\pi}{3}=k\pi+\cfrac{\pi}{2}(k\in Z)\)，得到\(f(x)\)对称轴方程为\(x=\cfrac{k\pi}{2}+\cfrac{\pi}{12}(k\in Z)\)；

令\(2x+\cfrac{\pi}{3}=k\pi(k\in Z)\)，得到\(f(x)\)的对称中心坐标为\((\cfrac{k\pi}{2}-\cfrac{\pi}{6}，1)(k\in Z)\)

函数 \(f(x)\)\(=\)\(\cos2x\)\(+\)\(a(sinx\)\(-\)\(cosx)\) 在区间 \([0，\cfrac{\pi}{2}]\) 上单调递增，求实数 \(a\) 的取值范围。

分析：【2019学生问题】[转化划归+恒成立问题+分离参数+换元法+求最值]

由于函数\(f(x)=cos2x+a(sinx-cosx)\)在区间\([0，\cfrac{\pi}{2}]\)上单调递增，

则\(f'(x)\ge 0\)在区间\([0，\cfrac{\pi}{2}]\)上恒成立，

又\(f'(x)=-2sin2x+a(cosx+sinx)\ge 0\)在区间\([0，\cfrac{\pi}{2}]\)上恒成立，

由于\(x\in [0，\cfrac{\pi}{2}]\)，\(cosx+sinx>0\)，故用完全分离参数法，得到，

\(a\ge \cfrac{2sin2x}{sinx+cosx}\)在区间\([0，\cfrac{\pi}{2}]\)上恒成立，

题目转化为求函数\(g(x)=\cfrac{2sin2x}{sinx+cosx}\)的最大值问题。

令\(sinx+cosx=t=\sqrt{2}sin(x+\cfrac{\pi}{4})\)，则\(t\in [1，\sqrt{2}]\)，

则\(sin2x=t^2-1\)，则函数\(g(x)=h(t)=\cfrac{2(t^2-1)}{t}=2(t-\cfrac{1}{t})\)，

又函数\(h'(t)=1+\cfrac{1}{t^2}>0\)在\(t\in [1，\sqrt{2}]\)上恒成立，

故函数\(h(t)\)在\(t\in [1，\sqrt{2}]\)上单调递增，

故\(g(x)_{max}=h(t)_{max}=h(\sqrt{2})=\sqrt{2}\)，

故\(a\ge \sqrt{2}\)。即\(a\in [\sqrt{2}，+\infty)\)。