函数的二阶导的使用情形

前言

学生在初次接触导数后，往往感觉是懵逼的，不知道导数是干什么的，对于函数的二阶导更是不知所云，本博文尝试初步解答这个困惑。

使用情形

• 情形一：二阶导全为正(或负)，就能判断一阶导的增(或减)，且一阶导的零点刚好在给定区间的端点处，这样一阶导就是全为正(或全为负)的，原函数就是单调函数；

【改编】已知函数 \(f(x)=\cfrac{2\ln x}{x}+\cfrac{1}{2}ax-2a-1(a>0)\)，当 \(a=2\) 时， 求证： \(f(x)\) 在 \([1,+\infty)\) 上单调递增；

证明 : 由已知 \(f(x)=\cfrac{2\ln x}{x}+x-5\)，限定定义域为\([1,+\infty)\) ，

\(f'(x)=\cfrac{2-2\ln x}{x^{2}}+1=\cfrac{x^{2}+2-2\ln x}{x^{2}}\)，

设 \(h(x)=x^{2}+2-2\ln x\)此时为何要取分子求其导数，原因是分母的正负我们已经能确定了；另外，从数的角度解不等式不好解，从形的角度不好做图像判断正负，所以利用二阶导判断其正负；，

\(h'(x)=2x-\cfrac{2}{x}=\cfrac{2\left(x^{2}-1\right)}{x}\)，

当 \(x \geqslant 1\) 时， \(h'(x)\geqslant 0\)， \(h(x)\) 在 \([1,+\infty)\) 上单调递增，

\(h(x)\geqslant h(1)=3>0\)

所以 \(x\geqslant 1\) 时, \(f'(x)>0\)， \(f(x)\) 单调递增 .

〔解释说明〕：本题目中，二阶导\(h'(x)\)\(\geqslant\)\(0\)，则可知一阶导\(h(x)\)[即\(f'(x)\)]单调递增，而一阶导的端点值\(h(1)\)\(=\)\(3\)\(>\)\(0\)[即\(f'(1)\)\(>\)\(0\)]，则说明在\(x\)\(\geqslant\)\(1\)时，\(f'(x)\)\(>\)\(0\)，故原函数\(f(x)\)单调递增，得证。

• 情形二：二阶导全为正(或负)，能判断一阶导的增(或减)，但此时一阶导的零点在给定区间内部，不在端点处，则一阶导有正有负，原函数就不是单调函数；

已知函数 \(f(x)=x+\cfrac{a+1}{x}-a\ln x\)， \(a\in R\).

(1). 求 \(f(x)\) 的单调性;

解: \(f'(x)=1-\cfrac{a+1}{x^{2}}-\cfrac{a}{x}=\cfrac{x^{2}-ax-(a+1)}{x^{2}}\)

\(=\cfrac{(x+1)[x-(a+1)]}{x^{2}}\)，\((x>0)\)，

① 当\(a+1\leqslant 0\)时，即 \(a \leqslant-1\) 时， \(f'(x)\geqslant 0\) 恒成立，\(\therefore f(x)\) 在 \((0,+\infty)\) 上单调递增；

② 当\(a+1>0\)时，即\(a>-1\) 时， 令 \(f'(x)<0\)， 则 \(0<x<a+1\)， 令 \(f'(x)>0\)， 则 \(x>a+1\)，

所以，\(f(x)\) 在 \((0, a+1)\) 上单调递减， 在 \((a+1,+\infty)\) 上单调递增；

综上: 当 \(a\leqslant-1\) 时， \(f(x)\) 在 \((0,+\infty)\) 上单调递增；

当 \(a>-1\) 时， \(f(x)\) 在 \((0, a+1)\) 上单调递减， 在 \((a+1,+\infty)\) 上单调递增 .

(2). 若 \(a>0\)， 且 \(f(x)\) 的最小值小于 \(4-2\ln 3\)， 求 \(a\) 的取值范围 .

解： 由 (1) 知 \(f(x)_{\min}=f(a+1)=a+1+1-a\ln(a+1)\)，

则\(a+2-a\ln(a+1)<4-2\ln2\)， 即 \(a-a\ln (a+1)<2-2\ln 3\)，

令 \(g(x)=x-x\ln(x+1)\)，\(x>-1\)，

则\(g'(x)=1-\ln(x+1)-\cfrac{x}{x+1}=-\ln(x+1)+\cfrac{1}{x+1}\)，

令 \(h(x)=-\ln(x+1)+\cfrac{1}{x+1}\)， \(h'(x)=-\cfrac{1}{x+1}-\cfrac{1}{(x+1)^{2}}<0\)，

所以 \(h(x)\) 在 \((-1,+\infty)\) 上单调递减， 又 \(h(0)=1>0\)， \(h(1)=\cfrac{1}{2}-\ln2<0\)此处使用函数的零点存在性定理，目的为确定函数在区间\((0,1)\)内的零点。，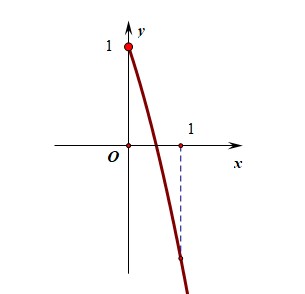

所以存在 \(x_{0}\in(0,1)\)， 使得 \(h\left(x_{0}\right)=0\)，

即 \(g'\left(x_{0}\right)=0\)， \(g(x)\)在 \(\left(0, x_{0}\right)\) 上单调递增， 在 \(\left(x_{0},+\infty\right)\) 上单调递减利用单调性做出函数的大致示意图，如图所示，，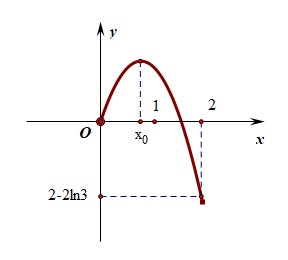

又 \(g(0)=0>2-2\ln 3\)， \(g(2)=2-2\ln 3\)，

所以，\(g(a)<2-2\ln3\) \(\Leftrightarrow\) \(a>2\)

所以，\(a\) 的取值范围为 \((2,+\infty)\) .

典例剖析

(2017\(\cdot\)北京卷)已知函数\(f(x)=e^xcosx-x\).

(1)、求曲线\(y=f(x)\)在点\((0，f(0))\)处的切线方程。

(2)、求函数\(f(x)\)在区间\([0，\cfrac{\pi}{2}]\)上的最大值和最小值。

分析：(1)由题目可知，\(f'(x)=e^xcosx+e^x\cdot (-sinx)-1=e^x(cosx-sinx)-1\)

则切线的斜率\(k=f'(0)=e^0(cos0-sin0)-1=0\)，

又\(f(0)=(e^xcosx-x)_{|x=0}=1\)，即切点为\((0，1)\)，

由点斜式可知切线方程为\(y-1=0(x-0)\)，

整理得到在点\((0，f(0))\)处的切线方程为\(y=1\)。

(2)由上可知，\(f'(x)=e^x(cosx-sinx)-1\)，

令\(h(x)=e^x(cosx-sinx)-1\)，

则\(h'(x)=e^x(cosx-sinx)+e^x(-sinx-cosx)=-2e^xsinx\)，^[1]

当\(x\in (0，\cfrac{\pi}{2})\)时， 容易知道\(h'(x)=-2e^xsinx<0\)(注意恒有\(e^x>0\))，

即函数\(h(x)\)，也就是函数\(f'(x)\)，在\(x\in (0，\cfrac{\pi}{2})\)单调递减，

则\(x\in [0，\cfrac{\pi}{2}]\)时，\(h(x)\leq h(0)=0\)，即$f'(x)\leq 0 $恒成立，

即使\(f'(x)=0\)，也是仅仅在单独的端点处，不会影响函数\(f(x)\)的单调性。

则有函数\(f(x)\)在区间$ [0，\cfrac{\pi}{2}]$上单调递减，

故\(f(x)_{min}=f(\cfrac{\pi}{2})=-\cfrac{\pi}{2}\)，\(f(x)_{max}=f(0)=1\)。

---

1. 1、关于二阶导的那些事，由解答过程就能看出，函数\(h(x)\)是函数\(f(x)\)的一阶导数，那么函数\(h'(x)\)其实是函数\(f(x)\)的二阶导，由于高中阶段我们只接触学习了一阶导数，故答案中一般不出现二阶导\(f''(x)\)的表示形式，我们做答案是也需要注意这一点。
   2、为什么要用二阶导？平时我们的解题经验是一般只给函数\(f'(x)\)求一次导数得到\(f'(x)\)，然后求解导函数不等式，由导函数的正负就知道了原函数\(f(x)\)的单调性了；但是，不是所有的函数求一阶导后，导函数的正负我们就能一目了然，这时候往往需要针对导函数再求导，也就是二阶导，其目的就是想知道导函数的单调性，在我们的解题体验中，往往是二阶导恒为正或恒为负，这样我们就知道了一阶导的单调性，利用一阶导的端点值(往往为0)，从而知道了一阶导的正负，这样原函数的单调性就清楚了。
   3、由于上述比较拗口，结合题目做以说明。原函数为\(f(x)\)，一阶导为\(f'(x)=h(x)\)，二阶导为\(h'(x)=f''(x)\)，
   由于二阶导\(h'(x)=f''(x)=-2e^xsinx<0\)在\((0，\cfrac{\pi}{2})\)上恒成立，则一阶导\(h(x)=f'(x)\)在\([0，\cfrac{\pi}{2}]\)上单调递减；
   此时一阶导\(h(x)=f'(x)\)有最值，取哪一个最值，一般取函数值为0的那一个。比如\(h(x)_{max}=h(0)=0\)，
   从而知道一阶导\(f'(x)<0\)，这样就知道了原函数\(f(x)\)在\([0，\cfrac{\pi}{2}]\)上单调递减；
   接下来求最值，那还不是小菜一碟吗。 ↩︎