三角形的某角取到最大值|题型

前言

当三角函数题目中有关键词“三角形某角取到最大值[可引申为或求最小值]时”，这类题目常要用到这个角的某种三角函数 [或正弦、或余弦、或正切] 的单调性，至于到底要用到哪一种，取决于题目的给定条件和变形方向，同时此类题目也常会用到均值不等式求题目中的最值.

线线角或线面角或面面角取到最大或者最小值，都可以依托上述的思路来转化；

另外，请注意参阅和总结关于分式的常用变形；

典例剖析

【2019届宝鸡市高三理科数学质检Ⅱ第16题】已知三角形的内角 \(A、B、C\) 所对的对边分别是 \(a、b、c\) ，若 \(a=\sqrt{2}\) ， \(b^2-c^2=6\) ，则角 \(A\) 取得最大值时，三角形 \(ABC\) 的面积为_________。

分析：由 \(cosA=\cfrac{b^2+c^2-a^2}{2bc}=\cfrac{b^2+c^2-2}{2bc}\)

\(=\cfrac{b^2+c^2-\cfrac{b^2-c^2}{3}}{2bc}=\cfrac{b^2+2c^2}{3bc}\geqslant \cfrac{2\sqrt{2}}{3}\)，

即 \(cosA\) 的最小值为 \(\cfrac{2\sqrt{2}}{3}\) ，当且仅当 \(b=\sqrt{2}c\) 且 \(b^2-c^2=6\) ，

即 \(b=2\sqrt{3}\) ， \(c=\sqrt{6}\) 时取到等号；此时 \(A\) 取到最大值，\(sinA=\cfrac{1}{3}\)，

故\(S_{\triangle ABC}=\cfrac{1}{2}bcsinA=\cfrac{1}{2}\times 2\sqrt{3}\times \sqrt{6}\times \cfrac{1}{3}=\sqrt{2}\)。

反思：①常数代换，由\(2=\cfrac{6}{3}=\cfrac{b^2-c^2}{3}\)，之所以做常数代换，是为了整理后便于使用均值不等式求\(cosA\)的最值。

【2020 \(\cdot\) 安徽名校联盟联考】在 \(\triangle ABC\) 中，角 \(A\)，\(B\)，\(C\) 所对的边分别为 \(a\)， \(b\)， \(c\)， 若 \(bc\)\(=\)\(1\)，\(b\)\(+\)\(2c\cos A\)\(=\)\(0\)， 则当角 \(B\) 取得最大值时， \(\triangle ABC\) 的周长为【\(\quad\)】

$A.2+\sqrt{3}$ $B.2+\sqrt{2}$ $C.3$ $D.3+\sqrt{2}$

解析： 由题意可得， \(\sin B+2\sin C\cos A=0\)，

即 \(\sin(A+C)+2\sin C\cos A=0\)，

得 \(\sin A\cos C=-3\sin C\cos A\)， 即 \(\tan A=-3\tan C\)，

又 \(\cos A=-\cfrac{b}{2c}<0\)，所以角 \(A\) 为钝角，于是 \(\tan C>0\)，

从而 \(\tan B=-\tan(A+C)=-\cfrac{\tan A+\tan C}{1-\tan A\tan C}\)

\(=\cfrac{2\tan C}{1+3\tan^{2}C}\)

\(=\cfrac{2}{\cfrac{1}{\tan C}+3\tan C}\),

由基本不等式， 得 \(\cfrac{1}{\tan C}+3\tan C\geqslant 2\sqrt{\cfrac{1}{\tan C}\times 3\tan C}=2\sqrt{3}\)，

当且仅当 \(\tan C=\cfrac{\sqrt{3}}{3}\) 时， 等号成立，

即 \(\tan B\leqslant \cfrac{2}{2\sqrt{3}}=\cfrac{\sqrt{3}}{3}\)，由于 \(y=\tan x\)在 \((0,\cfrac{\pi}{2})\)上单调递增，

故此时角 \(B\) 取得最大值， 且 \(\tan B=\tan C=\cfrac{\sqrt{3}}{3}\)， \(\tan A=-\sqrt{3}\)，

即 \(b=c\)， \(A=120^{\circ}\)， 又 \(bc=1\)，

所以 \(b=c=1\)， \(a=\sqrt{3}\)， 故 \(\triangle ABC\) 的周长为 \(2+\sqrt{3}\).

在\(\Delta ABC\)中，角\(A、B、C\)的对边分别为\(a、b、c\)，若\(b=1\)，\(a=2c\)，则当\(C\)取最大值时，\(\Delta ABC\)的面积为【】

$A、\cfrac{\sqrt{3}}{3}$ $B、\cfrac{\sqrt{3}}{6}$ $C、\cfrac{2\sqrt{3}}{3}$ $D、\sqrt{3}$

分析：当 \(C\) 取到最大值时， \(cosC\) 取得最小值，故先研究 \(cosC\) ，

\(cosC=\cfrac{a^2+b^2-c^2}{2ab}=\cfrac{3c^2+1}{4c}\)

\(=\cfrac{1}{4}(3c+\cfrac{1}{c})\ge \cfrac{1}{4}\cdot 2\sqrt{3}=\cfrac{\sqrt{3}}{2}\)，

当且仅当\(3c=\cfrac{1}{c}\)，即\(c=\cfrac{\sqrt{3}}{3}\)时取得等号；

且此时\(sinC=\cfrac{1}{2}\)，故当\(C\)取到最大值时，

\(S_{\Delta ABC}=\cfrac{1}{2}absinC\)

\(=\cfrac{1}{2}\cdot 2c\cdot 1\cdot \cfrac{1}{2}=\cfrac{\sqrt{3}}{6}\)，

故选\(B\)。

【2021届高三文科小题满分练】 已知 \(\triangle ABC\) 的内角 \(A\)， \(B\)， \(C\) 的对边分别为 \(a\)， \(b\)， \(c\)， 若 \(2c\sin C\)\(=\)\((a+b)\)\((\sin B-\sin A)\)， 则当角 \(C\) 取得最大值时， \(B\) 等于【 \(\quad\) 】

$A.\cfrac{\pi}{3}$ $B.\cfrac{\pi}{6}$ $C.\cfrac{\pi}{2}$ $D.\cfrac{2\pi}{3}$

解析： 由 正弦定理角化边，得 \(2c^{2}=(a+b)(b-a)\)，

即 \(b^{2}-a^{2}=2 c^{2}\)，即\(c^2=\cfrac{b^2-a^2}{2}\)，

则由余弦定理得，

\[\cos C=\cfrac{a^{2}+b^{2}-c^{2}}{2ab}=\cfrac{3a^{2}+b^{2}}{4ab}\geqslant\cfrac{2\sqrt{3a^{2}\cdot b^{2}}}{4ab}=\cfrac{\sqrt{3}}{2} \]

当且仅当 \(b=\sqrt{3}a\) 时等号成立，则易知角 \(C\) 的最大值为 \(\cfrac{\pi}{6}\).

当 \(b=\sqrt{3}a\) 时， \(3a^{2}-a^{2}=2c^{2}\)， 则 \(a=c\)，

所以 \(A=C=\cfrac{\pi}{6}\)， \(B=\pi-\cfrac{\pi}{6}-\cfrac{\pi}{6}=\cfrac{2\pi}{3}\)， 故选 \(D\).

【2024高一训练题目】如图，在正方体 \(ABCD-A_1B_1C_1D_1\) 中，点 \(F\) 是线段 \(BC_1\) 上的动点，则直线 \(A_1F\) 与平面 \(BDC_1\) 所成的最大角的余弦值为___________.

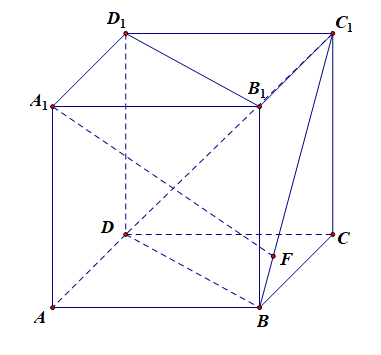
解：如图所示，利用正方体中储备的知识 ^[1]很容易想到，连接 \(A_1C\)，则可知体对角线 \(A_1C\perp\) 平面 \(BC_1D\)，令垂足为点 \(O\)，连接 \(OF\) ，则直线 \(A_1F\) 与平面 \(BDC_1\) 所成的角为 \(\angle A_1FO\)，为了求 \(\angle A_1FO\) 的最大值，可以考虑两个角度：其一，从形上思考，在等边 \(\triangle DC_1B\) 中，当动点 \(F\) 靠近点 \(B\) 或点 \(C_1\) 时 \(\angle A_1FO\) 越来越小(可以借助极端的情形思考，让线段 \(BC_1\) 非常长，则角的顶点就近乎在无限远处，其大小就接近 0 了)，那么在线段的中点位置时[其实是 \(OF\perp BC_1\) 时，为什么这样可以从思路二中得到解答和印证]，\(\angle A_1FO\) 达到最大，为便于计算，令 \(AB=1\)，则 \(A_1C=\sqrt{3}\)，\(A_1O\)\(=\)\(\cfrac{2}{3}A_1C\)\(=\)\(\cfrac{2\sqrt{3}}{3}\)，\(BD\)\(=\)\(\sqrt{2}\)，则 \(BF\)\(=\)\(\cfrac{2}{2}\)，\(DF\)\(=\)\(\cfrac{6}{2}\)，则 \(OF\)\(=\)\(\cfrac{1}{3}DF\)\(=\)\(\cfrac{\sqrt{6}}{6}\)，又由\(Rt\triangle A_1B_1F\) 可得 \(A_1F\)\(=\)\(\cfrac{\sqrt{6}}{2}\)，故 \(\cos\angle A_1FO\)\(=\)\(\cfrac{OF}{A_1F}\)\(=\)\(\cfrac{1}{3}\)；

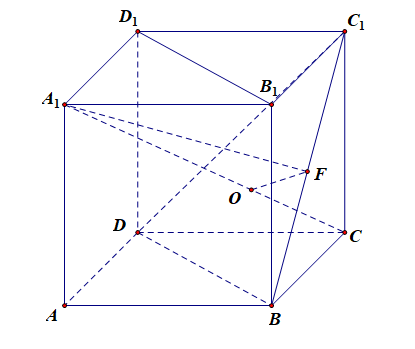
其二，从数上思考，由上述可知所求的线面角为 \(\angle A_1FO\)，在 \(Rt\triangle A_1FO\) 中，由于 \(A_1O\) 的长度为定值，故可设 \(A_1O\)\(=\)\(a\)，\(OF\)\(=\)\(x\)，则 \(A_1F\)\(=\)\(\sqrt{x^2+a^2}\)，这样 \(\cos\angle\)\(A_1FO\)\(=\)\(\cfrac{OF}{A_1F}\)\(=\)\(\cfrac{x}{\sqrt{x^2+a^2}}\)\(=\)\(\sqrt{\cfrac{x^2}{x^2+a^2}}\)\(=\)\(\sqrt{\cfrac{x^2+a^2-a^2}{x^2+a^2}}\)\(=\)\(\sqrt{1-\cfrac{a^2}{x^2+a^2}}\).

由于 \(a\) 为常数，故当 \(x>0\) 时，\(x\nearrow\)，\(x^2\nearrow\)，\(x^2+a^2\nearrow\)，\(\cfrac{a^2}{x^2+a^2}\searrow\)，\(-\cfrac{a^2}{x^2+a^2}\nearrow\)，\(1-\cfrac{a^2}{x^2+a^2}\nearrow\)，\(\sqrt{1-\cfrac{a^2}{x^2+a^2}}\nearrow\)，故当 \(x\nearrow\)，\(\cos\angle\)\(A_1FO\nearrow\)，又由于 \(y=\cos x\) 为 \([0,\cfrac{\pi}{2}]\) 上的减函数，故如果要 \(\angle\)\(A_1FO\) 最大，则需要 \(\cos\angle\)\(A_1FO\) 最小，即需要 \(x\) 最小，这样就需要 \(OF\) 最小，而直线外一点和直线上的动点之间的点点距中只有垂线段最短，故需要 \(OF\perp BC_1\)， 依托思路一求得 \(A_1O=\cfrac{2\sqrt{3}}{3}\)，\(OF\)\(=\)\(\cfrac{\sqrt{6}}{6}\)，代入求得 \(\cos\angle A_1FO\)\(=\)\(\cfrac{OF}{A_1F}\)\(=\)\(\cfrac{1}{3}\)；

---

1. 比如，积累正方体中体对角线 \(A_1C\perp\) 平面 \(BC_1D\)，且知道 \(A_1O=\cfrac{2}{3}A_1C\)，等等，数学学习中的好多东西是需要积累的； ↩︎