分形图与二阶数列

前言

涉及数列类的归纳推理，常常考查二阶等差数列已知数列\(\{a_n\}\)，不是等差数列，但是\((a_{n+1}\)\(-\)\(a_n)\)\(-\)\((a_n\)\(-\)\(a_{n-1})\)\(=\)\(d\)，\(d\)为常数，则数列\(\{a_{n+1}\)\(-\)\(a_n\}\)相对于数列 \(\{a_n\}\)，就可以称为二阶数列，且其为等差数列，故称为二阶等差数列。，或二阶等比数列已知数列\(\{a_n\}\)，不是等比数列，但是\(\cfrac{a_{n+1}-a_n}{a_n-a_{n-1}}\)\(=\)\(q\)，\(q\)为常数，则数列\(\{a_{n+1}\)\(-\)\(a_{n}\}\)为原数列\(\{a_n\}\)的二阶等比数列；，或斐波那契数列斐波那契数列又称黄金分割数列，因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是数列 \(1\) , \(1\) , \(2\) , \(3\) , \(5\) , \(8\) , \(13\) , \(\cdots\)，在数学上，斐波纳契数列以递归的方法定义 \(a_1=1\)，\(a_2=1\)，且满足 \(a_{n+1}\) \(=\) \(a_n\) \(+\) \(a_{n-1}\)，\(n\) \(\geqslant\) \(2\)；

典例剖析

【与斐波那契数列有关的归纳推理】某种树的分枝生长规律如图所示，第1年到第5年的分枝数分别为\(1，1，2，3，5\)，则预计第10年树的分枝数为

$A.21$ $B.34$ $C.52$ $D.55$

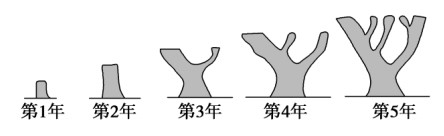
分析：本题目涉及到的数列为“斐波那契数列”，^[1]

其构成规律为：\(a_1=1\)，\(a_2=1\)已知，其他项由递推公式\(a_{n+2}\)\(=\)\(a_{n+1}\)\(+\)\(a_n\)，\(n\in N^*\)得到，

故\(a_6=8\)，\(a_7=13\)，\(a_8=21\)，\(a_9=34\)，\(a_{10}=55\)，\(a_{11}=89\)，故选\(D\)。

【与二阶等差数列有关的归纳推理】【2018·大庆校级模拟】蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的截面图．其中第一个图有\(1\)个蜂巢，第二个图有\(7\)个蜂巢，第三个图有\(19\)个蜂巢，按此规律，第\(6\)幅图的蜂巢总数为【 】

$A.61$ $B.90$ $C.91$ $D.127$

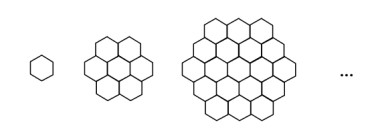
法1：注意到蜂巢个数所成的数列是二阶等差数列，我们可以这样做：

\(1\stackrel{+6}{\longrightarrow}7\)； \(7\stackrel{+2\times 6}{\longrightarrow}19\)；\(19\stackrel{+3\times 6}{\longrightarrow}37\)；\(37\stackrel{+4\times6}{\longrightarrow}61\)；\(61\stackrel{+5\times6}{\longrightarrow}91\)；\(91\stackrel{+6\times6}{\longrightarrow}127\)；故选\(C\)。

法2：利用二阶等差数列和累加法求解；

令蜂巢个数为\(f(n)\)，则\(f(1)=1\)，\(f(2)=7\)，\(f(3)=19\)，\(f(4)=37\)，由于

\(f(2)-f(1)=7-1=1\times 6\)；

\(f(3)-f(2)=19-7=2\times 6\)；

\(f(4)-f(3)=37-19=3\times 6\)；

\(f(5)-f(4)=61-37=4\times 6\)；

$\cdots $，

\(f(n)-f(n-1)=6\times (n-1)\)；

因此，当\(n\ge 2\)时，由累加法可知，

\(f(n)-f(1)=6\times [1+2+3+\cdots+(n-1)]=3n(n-1)\)；

故\(f(n)=3n^2-3n+1\)；

当\(n=1\)时，\(f(1)=1=3\times1^2-3\times1+1\)，符合上式，

故蜂巢个数为\(f(n)=3n^2-3n+1\)，

故可以计算\(f(6)=91\)，当然也可以得到\(f(10)=271\)；

【与二阶等差数列有关的归纳推理】在平面内有\(n(n\in N*)\)条直线，其中任何两条不平行，任何三条不过同一点，若这\(n\)条直线把平面分成\(f(n)\)个平面区域，试求\(f(1)\)，\(f(2)\)，\(f(3)\)，\(f(4)\)，\(f(5)\)的值；并总结\(f(n)\)的表达式。

解析：由题意知，则\(f(1)=2\)，\(f(2)=4\)，\(f(3)=7\)，\(f(4)=11\)，\(f(5)=16\)，

\(f(2)-f(1)=4-2=2\)；

\(f(3)-f(2)=7-4=3\)；

\(f(4)-f(3)=11-7=4\)；

\(f(5)-f(4)=16-11=5\)；

$\cdots $，

\(f(n)-f(n-1)=n\)；

因此，当\(n\ge 2\)时，由累加法可知，

\(f(n)-f(1)=2+3+\cdots+n=\cfrac{(n+2)(n-1)}{2}\)

即\(f(n)=\cfrac{n^2+n+2}{2}\)

当\(n=1\)时，\(f(1)=2\)，也满足上式，

故\(f(n)=\cfrac{n^2+n+2}{2}\)。

【与累加法有关的归纳推理】下面四个图案，都是由小正三角形构成，设第\(n\)个图形中所有小正三角形边上黑点的总数为\(f(n)\)．

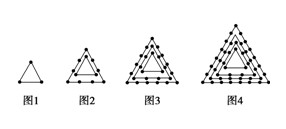
(1)求出\(f(2)\)，\(f(3)\)，\(f(4)\)，\(f(5)\)；

分析：由题意可知，

\(f(1)=3\)，

\(f(2)=f(1)+3+3\times 2=12\)，

\(f(3)=f(2)+3+3\times 4=27\)，

\(f(4)=f(3)+3+3\times 6=48\)，

\(f(5)=f(4)+3+3\times 8=75\)，

(2)找出\(f(n)\)与\(f(n＋1)\)的关系，并求出\(f(n)\)的表达式．

分析：由题意及(1)可知，

\(f(n+1)=f(n)+3+3\times 2n=f(n)+6n+3\)，

即\(f(n+1)-f(n)=6n+3\)，

则\(f(2)-f(1)=6\times 1+3\)，

\(f(3)-f(2)=6\times 2+3\)，

\(f(4)-f(3)=6\times 3+3\)，

\(\cdots\)，\(\cdots\)，

\(f(n)-f(n-1)=6\times (n-1)+3\)，

利用累加法可知，当\(n\ge 2\)时，

\(f(n)-f(1)=6[1+2+\cdots+(n-1)]+3(n-1)=6\times \cfrac{n(n-1)}{2}+3(n-1)=3n^2-3\)，

即\(f(n)=3n^2\)，当\(n=1\)时，满足上式，

故\(f(n)=3n^2(n\in N^*)\)。

【2021届高三文科一轮试题】【分形图】某种平面分形图如图所示，一级分形图是由一点出发的三条线段，长度均为\(1\)，两两夹角为\(120^{\circ}\)；二级分形图是从一级分形图的每条线段的末端出发，再生成两条长度为原来的线段，且这两条线段与原线段两两夹角为\(120^{\circ}\)，\(\cdots\)，依此规律人文得到\(n\)级分形图.

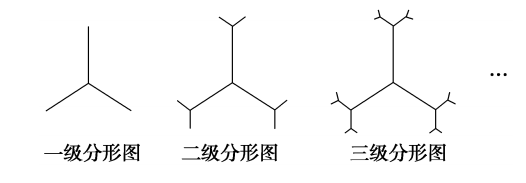
则 \(n\) 级分形图中共有__________条线段.

法1：归纳推理，由此分形图的制作过程我们可以得到以下的表达式，用\(f(n)\)表达\(n\)级分形图的线段条数，则有

\(f(1)=3\)；

\(f(2)=3+6\)；

\(f(3)=3+1\times 6+2\times 6\)；

\(f(4)=3+1\times 6+2\times 6+4\times 6\)；

\(f(5)=3+1\times 6+2\times 6+4\times 6+8\times 6\)；

\(\cdots\)，

\(f(n)=3+1\times 6+2\times 6+4\times 6+8\times 6+\cdots+2^{n-2}\times 6\)；

\(=3+6(1+2+2^2+2^3+\cdots+2^{n-2})=3+6\cfrac{1\cdot(2^{n-1}-1)}{2-1}=3\times 2^n-3\)

法2：由此分形图的制作过程我们可以得到以下的表达式，用\(f(n)\)表达\(n\)级分形图的线段条数，则有

\(f(1)=3\)；

\(f(2)=3+6\)；

\(f(3)=3+1\times 6+2\times 6\)；

\(f(4)=3+1\times 6+2\times 6+4\times 6\)；

\(f(5)=3+1\times 6+2\times 6+4\times 6+8\times 6\)；

\(\cdots\)，\(\cdots\)，

对以上数据做加工，得到如下，[其实是个二阶等比数列]

\(f(2)-f(1)=1\times 6=2^0\times 6\)；

\(f(3)-f(2)=2\times 6=2^1\times 6\)；

\(f(4)-f(3)=4\times 6=2^2\times 6\)；

\(f(5)-f(4)=8\times 6=2^3\times 6\)；

\(\cdots\)，\(\cdots\)，

\(f(n)-f(n-1)=? \times 6=2^{n-2}\times 6\)；

以上\(n-1\)个式子累加，得到

\(f(n)-f(1)=(2^0+2^1+2^2+\cdots+2^{n-2})\times 6=6\times \cfrac{2^{n-1}-1}{2-1}=6(2^{n-1}-1)\)，

解得， \(f(n)=6\cdot 2^{n-1}-6+3=3\times 2^n-3\)；

龙曲线是由一条单位线段开始， 按下面的规则画成的图形： 将前一代的每一条折线段都作为这一代的等腰直角三角形的斜边， 依次画出所有直角三角形的两段，使得所画的相邻两线段永远垂直 (即所画的直角三角形在前一代曲线的左右两边交替出现)。 例如第一代龙曲线 (图 1) 是以 \(A_{1}A_{2}\) 为斜边画出等腰直角三角形的直角边 \(A_{1}A_{3}\)， \(A_{3} A_{2}\) 所得的折线图， 图2、图 3 依次为第二代、第三代龙曲线 (虚线即为前一代龙曲线)， \(A_{1}, A_{2}, A_{3}\) 为第一代龙曲线的顶点， 设第 \(n\) 代龙曲线的顶点数为 \(a_{n}\)， 由图可知 \(a_{1}=3\)， \(a_{2}=5\)， 记数列 \(\{\cfrac{2^{n}}{a_{n}a_{n+1}}\}\) 的前 \(n\) 项和 \(S_{n}\)， 若实数 \(\lambda >S_{n}\) 恒成立， 则实数 \(\lambda\) 的取值范围是__________.

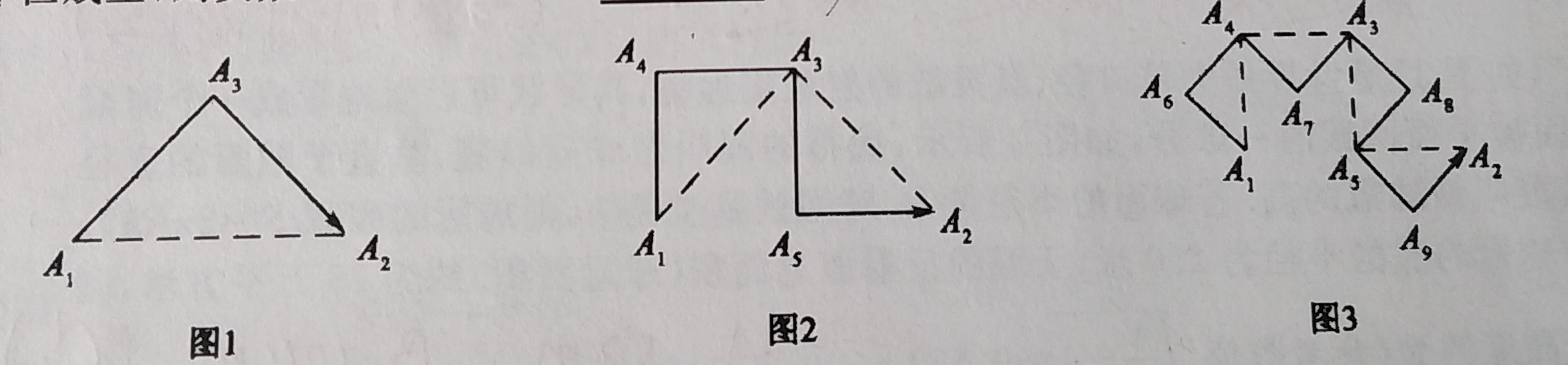
解析：由题可知，先从龙曲线的构成方式找关系得到[其实就是递推关系]，

\(a_{1}=3\) ， \(a_{2}=2\times a_{1}-1=2 \times 3-1=5\)，\(a_{3}=2 \times a_{2}-1=2(3 \times 2-1)-1=9\)，

\(a_{4}=2\times a_{3}-1=2\times 9-1=17\)， \(\cdots\)，

重新整理上述数据得到如下数列[总结归纳数列的通项公式]，

\(a_{1}=3=2^{1}+1\)， \(a_2=5=2^{2}+1\)， \(a_{3}=9=2^{3}+1\) ，\(a_{4}=17=2^{4}+1\)，

所以归纳猜想得到通项公式为 \(a_{n}=2^{n}+1\)

则 \(\cfrac{2^n}{{a_n}a_{n+1}}=\cfrac{2^n}{(2^n+1)(2^{n+1}+1)}\)\(=\cfrac{1}{2^n+1}-\cfrac{1}{2^{n+1}+1}\)

故 \(S_n=\cfrac{1}{2^1+1}-\cfrac{1}{2^2+1}+\cfrac{1}{2^2+1}-\cfrac{1}{2^3+1}+\cdots+\cfrac{1}{2^n+1}-\cfrac{1}{2^{n+1}+1}\)

\(=\cfrac{1}{3}-\cfrac{1}{2^{n+1}+1}\)，

由于 \(\lambda >S_n\) 恒成立， 则 \(\lambda\in [\cfrac{1}{3},+\infty)\) .

---

1. 斐波那契数列的通项公式的推导过程 ↩︎