三角函数性质研究中的容错处理

前言

在研究正弦型函数\(f(x)=A\sin(\omega x+\phi)+k\)的各种性质时，我们更多的利用整体思想，比如研究其值域，单调性，奇偶性，周期性等，但是当研究对称性时还是需要注意，容易出错；请参阅三角函数图像解题中横轴选 \(x\) 还是 \(\omega x+\phi\)

典例剖析

【2020\(\cdot\)东城区模拟】已知函数 \(f(x)=4\sin(x-\cfrac{\pi}{3})\cos x+\sqrt{3}\).

(1).求函数 \(f(x)\) 的最小正周期和单调递增区间；

分析：此处将化简作为重点加以说明，需要特别仔细认真，

\(f(x)=4\sin(x-\cfrac{\pi}{3})\cos x+\sqrt{3}\)

\(=4\left(\cfrac{1}{2}\sin x-\cfrac{\sqrt{3}}{2}\cos x\right)\cos x+\sqrt{3}\)

\(=2\sin x\cos x-2\sqrt{3}\cos^2x+\sqrt{3}\)

\(=\sin2x-\sqrt{3}\cos2x\)

\(=2\sin(2x-\cfrac{\pi}{3})\)；

故\(T=\pi\)，单调递增区间的具体求解过程略，为\([k\pi-\cfrac{\pi}{12},k\pi+\cfrac{5\pi}{12}](k\in Z)\)；

(2).若函数 \(g(x)=f(x)-m\) 在 \([0,\cfrac{\pi}{2}]\) 上有两个不同的零点 \(x_{1}\)， \(x_{2}\)，求实数 \(m\) 的取值范围，并计算 \(\tan(x_{1}+x_{2})\) 的值.

分析：函数 \(g(x)=f(x)-m\) 在 \([0, \cfrac{\pi}{2}]\) 上有两个不同的零点 \(x_{1}\)， \(x_{2}\)，

即函数 \(y=f(x)\) 与 \(y=m\)在\([0,\cfrac{\pi}{2}]\)上的图像有两个不同的交点，

在直角坐标系中画出函数 \(y=f(x)=2\sin(2x-\cfrac{\pi}{3})\) 在\([0, \cfrac{\pi}{2}]\)上的图像此处容易产生作图的冲突，到底以哪个为横轴做图像，如果以 \(2x\)\(-\)\(\cfrac{\pi}{3}\) 为横轴做图像快捷但容易出错，若以 \(x\) 为横轴做图像要慢得多但不容易出错，详细见下详述；，

如图所示，由图像可知，当且仅当 \(m\in[\sqrt{3}, 2)\) 时，方程 \(f(x)=m\) 有两个不同的解\(x_{1}\)， \(x_{2}\)，

又由于对称轴为\(x=\cfrac{5\pi}{12}\)，则有\(x_{1}+x_{2}=2\times\cfrac{5\pi}{12}=\cfrac{5\pi}{6}\)，

故\(\tan(x_{1}+x_{2})=\tan\cfrac{5\pi}{6}=-\tan\cfrac{\pi}{6}=-\cfrac{\sqrt{3}}{3}\).

[有误区的解法]用整体思想求解，接上题，

函数 \(y=f(x)=2\sin(2x-\cfrac{\pi}{3})\) 与 \(y=m\)在\([0,\cfrac{\pi}{2}]\)上的图像有两个不同的交点，

以\(2x-\cfrac{\pi}{3}\)为横轴，做出函数\(y=f(x)\)和\(y=m\)的图像，由图像可知，

由于\(0\leqslant x\leqslant \cfrac{\pi}{2}\)，\(-\cfrac{\pi}{3}\leqslant 2x-\cfrac{\pi}{3}\leqslant \cfrac{2\pi}{3}\)，

则\(-\sqrt{3}\leqslant 2\sin(2x-\cfrac{\pi}{3})\leqslant 2\)，由图可知，当\(\sqrt{3}\leqslant m<2\)时，两个函数的图像有两个交点，

即\(m\in[\sqrt{3}, 2)\) 时，方程 \(f(x)=m\) 有两个不同的解\(x_{1}\)， \(x_{2}\)，

但此时对称轴为\(x=\cfrac{\pi}{2}\)，故\(x_1+x_2=\pi\)，则\(\tan(x_1+x_2)=\tan\pi=0\)，出现错误；

【错因分析】受思维定势的影响，我们一般都认为两个交点的横坐标都是\(x\)，而上述的解法中横轴是\(2x-\cfrac{\pi}{3}\)，

故方程 \(f(x)=m\) 有两个不同的解\(2x_1-\cfrac{\pi}{3}\)， \(2x_2-\cfrac{\pi}{3}\)，

故\(\cfrac{(2x_1-\frac{\pi}{3})+(2x_2-\frac{\pi}{3})}{2}=\cfrac{\pi}{2}\)，

即\((2x_1-\cfrac{\pi}{3})+(2x_2-\cfrac{\pi}{3})=\pi\)，则有\(x_{1}+x_{2}=\cfrac{5\pi}{6}\)，

故\(\tan(x_{1}+x_{2})=\tan\cfrac{5\pi}{6}=-\tan\cfrac{\pi}{6}=-\cfrac{\sqrt{3}}{3}\).

【2022·高三数学二轮复习用题】设函数 \(f(x)=\sin(\omega x+\cfrac{\pi}{6})\)(\(\omega>0\))， 已知方程 \(f(x)=a(a\) 为常数 \()\) 在 \([0,\cfrac{7\pi}{6}]\) 上恰有三个根， 分别为 \(x_{1}\)， \(x_{2}\)， \(x_{3}\)，\((x_{1}<x_{2}<x_{3})\)， 下述四个结论：

①.当 \(a=0\) 时, \(\omega\) 的取值范围是 \([\cfrac{17}{7}, \cfrac{23}{7})\);

②.当 \(a=0\) 时, \(f(x)\) 在 \([0, \cfrac{7\pi}{6}]\) 上恰有 \(2\) 个极小值点和 \(1\) 个极大值点;

③.当 \(a=0\) 时, \(f(x)\) 在 \([0, \cfrac{\pi}{12}]\) 上单调递增;

④.当 \(\omega=2\) 时, \(a\) 的取值范围为 \([\cfrac{1}{2}, 1)\), 且 \(x_{1}+2 x_{2}+x_{3}=\cfrac{5\pi}{3}\).

其中正确的结论为___________(填序号).

解析：仿上例中的法2，以 \(\omega x+\phi\) 为横轴作图求解；

当 \(0 \leqslant x \leqslant \cfrac{7 \pi}{6}\) 时， \(\cfrac{\pi}{6} \leqslant \omega x+\cfrac{\pi}{6} \leqslant \cfrac{7 \omega \pi}{6}+\cfrac{\pi}{6}\)，

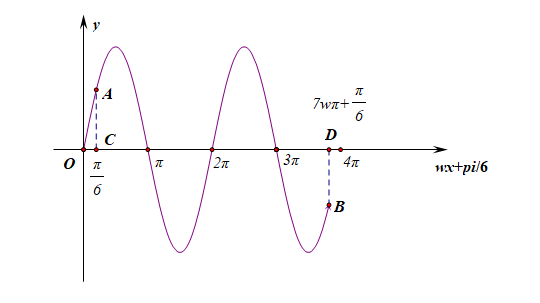
此时图像是曲线中的点 \(A\) 到点 \(B\) 之间的部分，落在横轴上的部分为 \([\cfrac{\pi}{6},\cfrac{7\omega\pi}{6}+\cfrac{\pi}{6}]\)，其中点 \(D\) 的横坐标 \(\cfrac{7\omega\pi}{6}+\cfrac{\pi}{6}\) 应该在区间 \([3\pi,4\pi)\) 之间活动，

此时由图像可知，若 \(f(x)\) 恰有 \(3\) 个零点， 则 \(3 \pi \leqslant \cfrac{7 \omega \pi}{6}+\cfrac{\pi}{6}<4\pi\)， 解得 \(\cfrac{17}{7} \leqslant \omega<\cfrac{23}{7}\)， 故 ① 正确；

且由图可知， \(f(x)\) 在 \([0,\cfrac{7\pi}{6}]\) 上恰有 \(2\) 个极大值点和 \(1\) 个(或 \(2\) 个)极小值点， 故 ② 错误；

当 \(x\in[0,\cfrac{\pi}{12}]\) 时， \(\cfrac{\pi}{6} \leqslant \omega x+\cfrac{\pi}{6} \leqslant \cfrac{\omega \pi}{12}+\cfrac{\pi}{6}\)，

由于 \(\cfrac{17}{7} \leqslant \omega<\cfrac{23}{7}\)，故 \(\omega x+\cfrac{\pi}{6}\) 的右端点的活动区间为 \(\cfrac{17}{7}\times\cfrac{\pi}{12}+\cfrac{\pi}{6}\)\(\leqslant\)\(\cfrac{\pi\omega}{12}+\cfrac{\pi}{6}\)\(<\)\(\cfrac{23}{7}\times\cfrac{\pi}{12}+\cfrac{\pi}{6}\)，

即\(\cfrac{31\pi}{84}\leqslant\)\(\cfrac{\pi\omega}{12}+\cfrac{\pi}{6}<\cfrac{37\pi}{84}<\cfrac{\pi}{2}\)，故 \([\cfrac{\pi}{6}, \cfrac{\omega \pi}{12}+\cfrac{\pi}{6}]\subsetneqq[0, \cfrac{\pi}{2}]\)，则 \(f(x)\) 在 \([0, \cfrac{\pi}{12}]\) 上单调递增， 故 ③ 正确；

当 \(\omega=2\) 时， \(2x+\cfrac{\pi}{6} \in[\cfrac{\pi}{6}, \cfrac{5\pi}{2}]\)， 画出函数的大致图象：

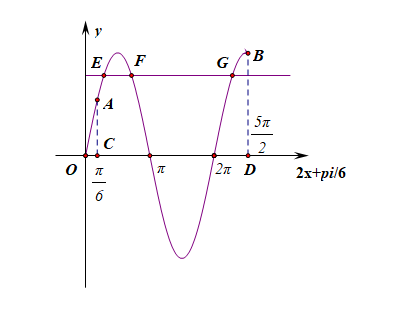
由图可知，要保证 \(f(x)=a\) 有三个交点，则 \(a\) 的取值范围为 \([\cfrac{1}{2}, 1)\)，且图上的三个交点 \(E\)、\(F\)、\(G\) 的横坐标应该依次为 \(2x_1+\cfrac{\pi}{6}\)， \(2x_2+\cfrac{\pi}{6}\)， \(2x_3+\cfrac{\pi}{6}\)，[原因是以 \(\omega x+\phi\) 为横轴作图]，且点 \(E\)、\(F\) 关于直线 \(x=\cfrac{\pi}{2}\) 对称，点 \(F\)、\(G\) 关于直线 \(x=\cfrac{3\pi}{2}\) 对称，

故由 \((2x_1+\cfrac{\pi}{6})+(2x_2+\cfrac{\pi}{6})=\pi\)，解得 \(x_{1}+x_{2}=\cfrac{\pi}{3}\)，

由 \((2x_2+\cfrac{\pi}{6})+(2x_3+\cfrac{\pi}{6})=3\pi\)，解得 \(x_{2}+x_{3}=\cfrac{4\pi}{3}\)，

所以 \(x_{1}+2 x_{2}+x_{3}=\cfrac{5\pi}{3}\)， 故 ④ 正确， 故填 ① ③ ④ .