在线|十月解答

前言

典例剖析

等腰梯形\(ABCD\)中， \(CD=\cfrac{1}{2}AB\)， \(E\)、\(F\) 分别是底边 \(AB\)、\(CD\) 的中点，如图所示, 把四边形 \(BEFC\)沿 \(EF\) 折起，使平面 \(BEFC\perp\)平面 \(ADFE\)， 如右图所示，若\(P \in\) 平面 \(BEFC\)，且\(PA\) 、\(PD\)与平面 \(BEFC\)所成的角相等，设为\(\theta(\theta \neq 0)\)，则动点\(P\)的轨迹是【\(\quad\)】

$A.\text{直线}$ $B.椭圆$ $C.圆$ $D.抛物线$

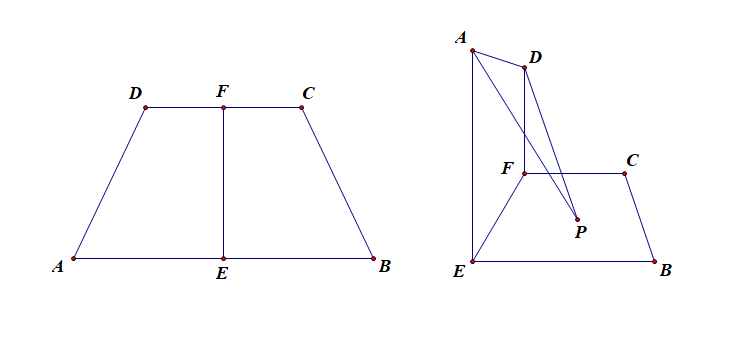
解：\(EF\perp DC\)， \(EF\perp AB\)，且平面 \(BEFC\perp\)平面 \(ADFE\)，\(AE\perp EF\)，

又有平面 \(BEFD\cap\) 平面\(AEFD=EF\)，故\(AE\perp\)面 \(BEFC\)， 又由于\(AE//FD\)

故\(FD\perp\) 面\(BEFC\)，则\(PA\)，\(PD\)与面 \(BEFC\) 所成角分别为 \(\angle APE\)和\(\angle DPF\)，

则 \(\angle APE=\angle DPF=\theta\)， 则\(tan\theta=\cfrac{AE}{EP}=\cfrac{DF}{FP}\)，

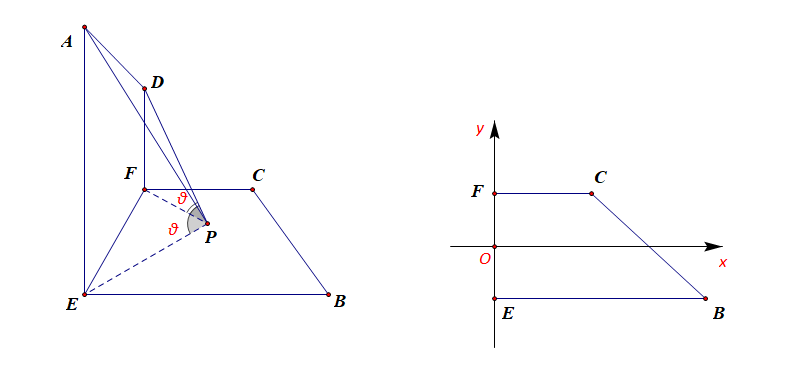
又由于 \(CD=\cfrac{1}{2}AB\)，则\(DF=\cfrac{1}{2}AE\)， 故\(EP=2FP\)；

以\(EF\) 所在直线为\(y\)轴， 以\(EF\) 的垂直平分线为\(x\) 轴建立如图所示的坐标系，

设 \(E(0,-m)\)， \(F(0, m)\)，\((m>0)\)， 再设\(P(x, y)\)，

则 \(|PE|^{2}=x^{2}+(y+m)^{2}\)，\(|PF|^{2}=x^{2}+(y-m)^{2}\)，

即 \(x^{2}+(y+m)^{2}=4[x^{2}+(y-m)^{2}]\)，

整理得到， \(3x^{2}+3y^{2}-10m y+3m^{2}=0\)，

再变形得到\(x^2+(y-\cfrac{5m}{3})^2=(\cfrac{4m}{3})^2\)，

即点 \(P\) 的轨迹为圆心\((0,\cfrac{5m}{3})\)，半径为\(R=\cfrac{4m}{3}\)的动圆，故选：\(C\).

解后反思：本题目到此，还可以求解圆的半径，圆的面积等；\(m\)为定值；

已知共面的三个单位向量\(\vec{a}\)，\(\vec{b}\)，\(\vec{c}\)满足\(\vec{a}\cdot\vec{b}\)\(=\)\(\vec{a}\cdot\vec{c}\)\(=\)\(\vec{b}\cdot\vec{c}\)\(=\)\(-\cfrac{1}{2}\)，若空间向量\(\vec{m}\)满足\(\vec{m}\cdot\vec{a}=\vec{m}\cdot\vec{c}\)，且对于任意\(x\)， \(y\in R\)，恒有\(|\vec{m}-(x\vec{a}+y\vec{b})|\)\(\geqslant\)\(|\vec{m}-\vec{a}-\vec{c}|\)\(=\)\(\sqrt{3}\)，则\(|\vec{m}-\vec{b}|\)=________.

分析：如图所示，由于三个单位向量共面，且满足\(\vec{a}\cdot\vec{b}\)\(=\)\(\vec{a}\cdot\vec{c}\)\(=\)\(\vec{b}\cdot\vec{c}\)\(=\)\(-\cfrac{1}{2}\)，

故三个向量的夹角分别为\(\cfrac{2\pi}{3}\)，且模长为\(1\)，令\(\overrightarrow{OA}=\vec{a}\)，\(\overrightarrow{OB}=\vec{b}\)，\(\overrightarrow{OC'}=\vec{c}\)，

以\(OA\)和\(OC'\)为邻边，做平行四边形\(OC'DA\)，则\(\overrightarrow{C'A}=\vec{a}-\vec{c}\)，\(\overrightarrow{OD}=\vec{a}+\vec{c}\)，

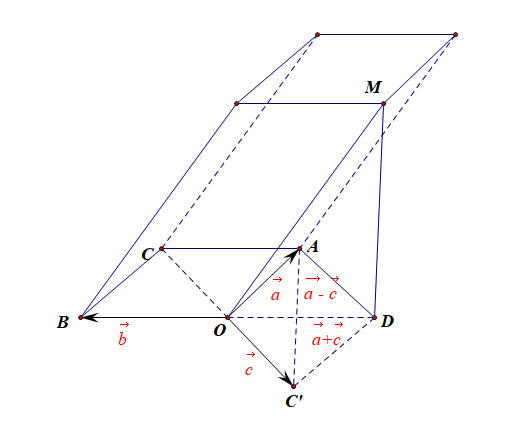
由于空间向量\(\vec{m}\)满足\(\vec{m}\cdot\vec{a}=\vec{m}\cdot\vec{c}\)，则有\(\vec{m}\cdot(\vec{a}-\vec{c})=0\)，

则点\(M\) 为如图所示的平行六面体的顶点，且\(\angle MOA=\angle MOC'\)，

又由于对于任意\(x\)， \(y\in R\)，恒有\(|\vec{m}-(x\vec{a}+y\vec{b})|\)\(\geqslant\)\(\sqrt{3}\)，

则必有\(MD\perp\)下底面\(OACB\)，且\(|\overrightarrow{MD}|=\sqrt{3}\)，

则在\(Rt\triangle OMD\)中，\(MD=\sqrt{3}\)，\(OD=1\)，故由勾股定理得到\(|OM|=2\)，

又\(|\vec{m}-\vec{b}|=|\overrightarrow{OM}-\overrightarrow{OB}|=|\overrightarrow{MB}|\)

在\(\triangle OMB\)中，\(OB=1\)，\(OMD=2\)，\(\angle BOM=120^{\circ}\)，

故由余弦定理得到\(|\vec{m}-\vec{b}|^2=|BM|^2=2^2+1^2-2\times2\times1\times\cos120^{\circ}=7\)，

故\(|\vec{m}-\vec{b}|=\sqrt{7}\).

解后反思：有空整理本题目中的数学语言；

正方体 \(ABCD-A_{1}B_{1}C_{1}D_{1}\)的棱长为\(1\)， 动点\(P\)，\(Q\) 分别在棱\(BC\)，\(CC_{1}\) 上， 过点 \(A\)， \(P\)， \(Q\) 的平面截该正方体所得的截面记为\(S\)，设\(BP=x\)， \(CQ=y\)，其中\(x\)， \(y\in[0,1]\)，下列命题:

①当 \(x=0\) 时， \(S\) 为矩形，其面积最大为 \(1\)；

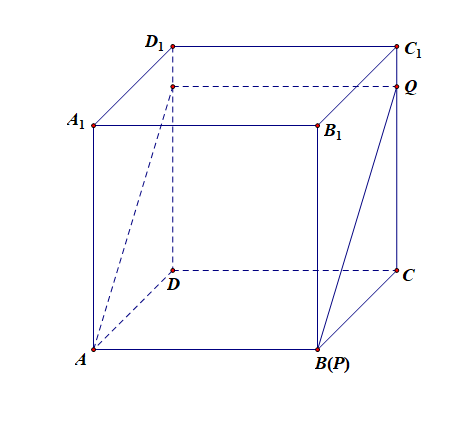
分析：当 \(x=0\) 时， \(S\) 为矩形，其面积最大时为矩形\(ABC_1D_1\)，故最大面积为\(\sqrt{2}\)，故①错误；

②当 \(x=y=\cfrac{1}{2}\) 时， \(S\) 为等腰梯形；

分析：如上图，由于\(x=y=\cfrac{1}{2}\)，容易证明\(AP=D_1Q\)，而\(PQ//AD_1\)，故截面\(S\) 为等腰梯形；故②正确；

③当 \(x=\cfrac{1}{2}\)，\(y\in(\cfrac{1}{2}, 1)\) 时, 设 \(S\) 与棱 \(C_{1}D_{1}\) 的交点为 \(R\)，则 \(RD_{1}=2-\cfrac{1}{y}\)；

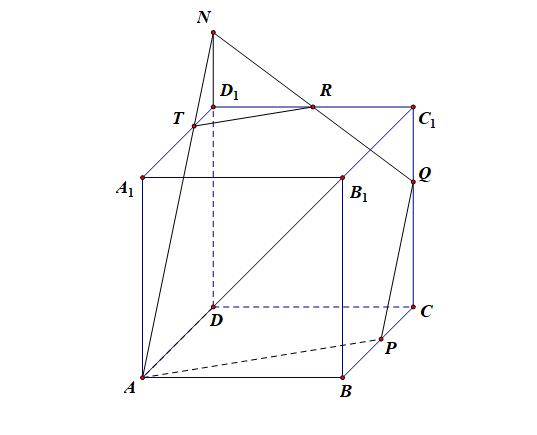
分析：设 \(S\) 与棱 \(C_{1}D_{1}\) 的交点为 \(R\)，延长\(DD_1\)，使\(DD_1\cap QR=N\)，

连接\(AN\)交\(A_1D_1\)于\(T\)，连接\(TR\)，可证\(AN//PQ\)一个平面和两个平行平面都相交，则所得的交线互相平行；\(\quad\)，

故可知\(\triangle PCQ\sim \triangle AD_1N\)，则\(\cfrac{PC}{AD}=\cfrac{CQ}{DN}=\cfrac{1}{2}\)，

即\(\cfrac{y}{DN}=\cfrac{1}{2}\)，故\(DN=2y\)，则\(D_1N=2y-1\)；

又由于\(\triangle NRD_1\sim \triangle QRC_1\)，可得\(\cfrac{C_1R}{D_1R}=\cfrac{C_1Q}{D_1N}\)，

令\(RD_1=x\)，即\(\cfrac{1-x}{x}=\cfrac{1-y}{2y-1}\)，利用合比定理，得到

\(\cfrac{1-x+x}{x}=\cfrac{1-y+2y-1}{2y-1}\)，即\(\cfrac{1}{x}=\cfrac{y}{2y-1}\)

可得\(x=RD_1=2-\cfrac{1}{y}\)，故③正确；

④当 \(y=1\) 时， 以 \(B_1\)为顶点，\(S\) 为底面的棱锥的体积为定值\(\cfrac{1}{3}\)； 其中正确的命题为_______________.

分析：当 \(y=1\) 时， 以 \(B_1\)为顶点，\(S\) 为底面的棱锥\(B_1-PC_1MA\)的体积为

\(V_{B_1-PC_1MA}=2V_{B_1-PC_1M}=2V_{P-B_1C_1M}\)

\(=2\times\cfrac{1}{3}\times\cfrac{1}{2}\times 1\times 1\times 1\)

\(=\cfrac{1}{3}\)，故④正确；

综上所述，真命题为②③④；

如图，四边形\(ABCD\)为正方形，\(MA//PB\)， \(MA\perp BC\)， \(AB\perp PB\)，\(MA=1\)， \(AB=PB=2\)；

(I). 求证: \(PB\perp\) 平面 \(ABCD\)；

因为 \(MA\perp BC\)， \(MA//PB\)， 所以 \(PB\perp BC\)，

又因为 \(PB\perp AB\)， \(AB\cap BC=B\)，\(AB\subsetneqq\)平面\(ABCD\)，\(BC\subsetneqq\)平面\(ABCD\)，

所以 \(PB\perp\) 平面 \(ABCD\).

(II).求直线 \(PC\) 与平面 \(PDM\) 所成角的正弦值.

解：因为 \(PB\perp\) 平面 \(ABCD\), \(AB\subsetneqq\) 平面 \(ABCD\), \(AD\subsetneqq\) 平面 \(ABCD\),

所以 \(PB\perp AB\), \(PB\perp AD\).

因为四边形 \(ABCD\) 为正方形, 所以 \(AB\perp BC\).

如图建立空间直角坐标系 \(B-xyz\),

则 \(P(0,0,2)\), \(M(2,0,1)\), \(C(0,2,0)\), \(D(2,2,0)\)

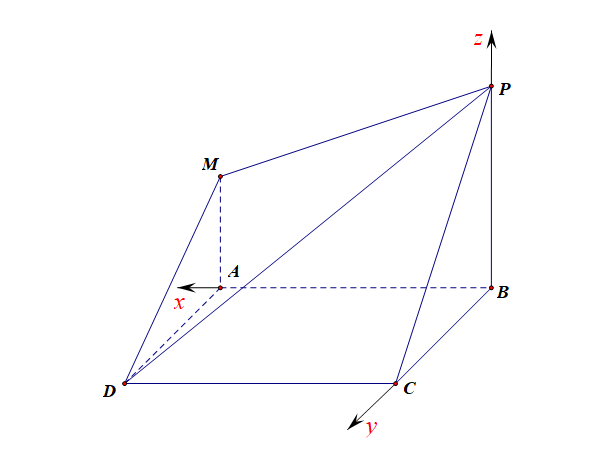
\(\overrightarrow{PC}=(0,2,-2)\), \(\overrightarrow{PD}=(2,2,-2)\), \(\overrightarrow{P M}=(2,0,-1)\)

设平面 \(PDM\) 的法向量为\(\vec{\mu}=(x, y,z)\), \(\left\{\begin{array}{l}\vec{\mu} \cdot \overrightarrow{PD}=0 \\ \vec{\mu} \cdot \overrightarrow{PM}=0\end{array}\right.\)，

即\(\left\{\begin{array}{l}2x+2y-2z=0 \\ 2x-z=0\end{array}\right.\)，

令 \(z=2\)， 则 \(x=1\), \(y=-1\) ，于是 \(u=(1,1,2)\)，平面 \(PDM\) 的法向量为 \(\vec{\mu}=(1,1,2)\)，

设直线 \(PC\)与平面 \(PDM\) 所成的角为 \(\theta\)，所以 \(\sin\theta=\cfrac{\overrightarrow{PC}\cdot \vec{\mu}}{|\overrightarrow{PC}|\cdot|\vec{\mu}|}=\cfrac{\sqrt{3}}{6}\).

所以直线 \(PC\) 与平面 \(PDM\) 所成角的正弦值为 \(\cfrac{\sqrt{3}}{6}\).

解后反思：本题目如果用几何法求解，难度比较大，遂放弃；

在正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中， \(E\)是侧面\(ADD_1A_{1}\) 内的动点，且\(B_1E//\)平面 \(BDC_1\)， 则直线 \(B_1E\) 与直线 \(AB\) 所成角的正弦值的最小值是【\(\quad\)】.

$A.\cfrac{1}{3}$ $B.\cfrac{\sqrt{3}}{3}$ $C.\cfrac{1}{2}$ $D.\cfrac{\sqrt{2}}{2}$

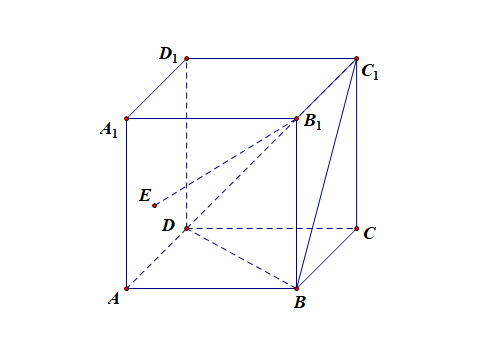
解：以\(D\)为坐标原点， 以\(DA\)所在直线为\(x\) 轴， 以\(DC\)所在直线 为 \(y\) 轴， 以\(DD_{1}\)所在直线 为z轴， 建立空间直角坐标系，

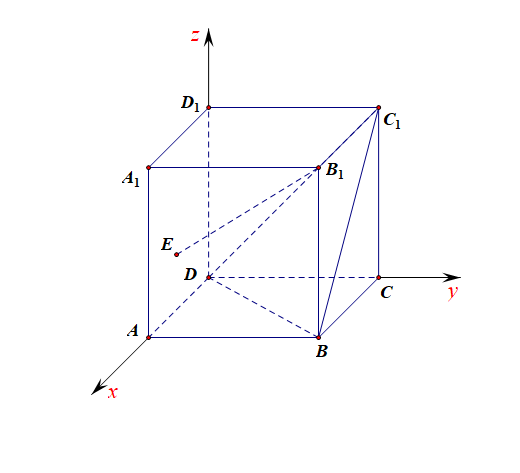
设正方体 \(ABCD-A_{1}B_{1}C_{1}D_{1}\) 中棱长为\(1\)，

设 \(E(a, 0, c)\)， \(0\leqslant a \leqslant 1\)，\(0 \leqslant c \leqslant 1\)，

\(B_{1}(1,1,1)\)，\(B(1,1,0)\)，\(D(0,0,0)\)，\(C_{1}(0,1,1)\)，

\(\overrightarrow{B_{1}E}=(a-1,-1, c-1)\)，\(\overrightarrow{DB}=(1,1,0)\)，\(\overrightarrow{DC_{1}}=(0,1,1)\)

设平面 \(DBC_{1}\)的法向量\(\vec{n}=(x, y, z)\)，

则 \(\left\{\begin{array}{l}\vec{n}\cdot\overrightarrow{DB}=x+y=0\\\vec{n}\cdot\overrightarrow{DC_{1}}=y+z=0\end{array}\right.\)，取 \(x=1\)，得\(\vec{n}=(1,-1,1)\)，

由于\(B_{1}E//\)平面\(BDC_{1}\)，故\(\overrightarrow{B_1E}\cdot \vec{n}=a-1+1+c-1=0\)，得到\(a+c=1\)，

所以\(a^{2}+c^{2}=(a+c)^{2}-2ac=1-2ac\)，\(ac\leqslant(\cfrac{a+c}{2})^{2}=\cfrac{1}{4}\)

设直线\(B_{1}E\)与直线 \(AB\) 所成角为 \(\theta\)， 则\(\theta\in(0,\cfrac{\pi}{2}]\)，

由于\(\overrightarrow{AB}=(0,1,0)\), \(\cos\theta=\cfrac{|\overrightarrow{AB}\cdot\overrightarrow{B_{1}E}|}{|\overrightarrow{AB}| \cdot|\overrightarrow{B_{1}E}|}=\cfrac{1}{\sqrt{(a-1)^{2}+1+(c-1)^{2}}}\)

由于\(ac\leqslant(\cfrac{a+c}{2})^{2}=\cfrac{1}{4}\)，

故\(2-2ac\geqslant\cfrac{3}{2}\)，\(\cfrac{1}{2-2ac}\leqslant \cfrac{2}{3}\)，

故\(\sin\theta=\sqrt{1-\cfrac{1}{(a-1)^{2}+1+(c-1)^{2}}}=\sqrt{1-\cfrac{1}{a^{2}+c^{2}-2(a+c)+3}}\)

\(=\sqrt{1-\cfrac{1}{a^{2}+c^{2}+1}}=\sqrt{1-\cfrac{1}{2-2ac}}\geqslant\sqrt{1-\cfrac{2}{3}}=\cfrac{\sqrt{3}}{3}\)

则直线 \(B_{1}E\) 与直线 \(AB\) 所成角的正弦值的最小值是\(\cfrac{\sqrt{3}}{3}\)，故选：\(B\).

解后反思：有空补充用形来求解；

已知四棱锥\(P-ABCD\)中，底面是梯形， \(DC//AB\)，\(AB=BC=2DC=4\)，\(\angle ABC=90^{\circ}\)，\(BD\)与\(AC\)交于点\(F\)，平面\(PDC\perp\)平面\(ABCD\)，\(PD=PC\)，点\(G\)是\(AP\)上一点，且\(AG=2GP\)；

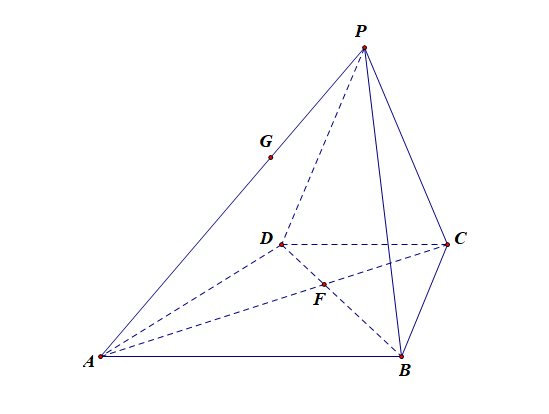
(1).求证: \(GF//\)平面\(PBC\)；

证明: 因为\(DC//AB\)， 所以\(\triangle ABF\sim \triangle CDF\)，则有\(\cfrac{AF}{FC}=\cfrac{AB}{DC}=2\)

又由于\(\cfrac{AF}{FC}=2=\cfrac{AG}{GP}\)，所以 \(GF//PC\)，

又\(GF\not\subset\)平面 \(PBC\)，\(PC\subsetneqq\) 平面 \(PBC\)，所以 \(GF//\)平面 \(PBC\)；

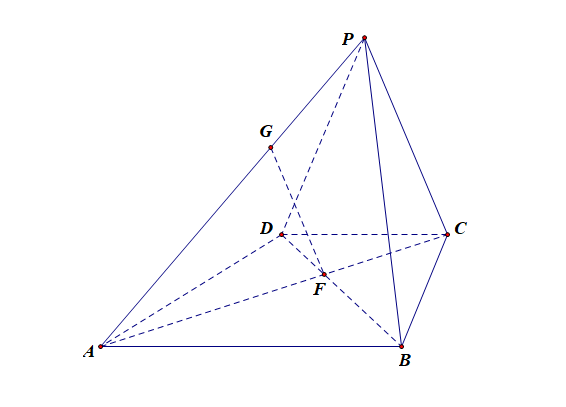
(2). 若二面角 \(P-AB-C\)为 \(45^{\circ}\)，

① 求直线 \(PC\) 与平面 \(PAB\) 所成角的正弦值；

解：取\(DC\)中点 \(O\)，并在平面 \(ABCD\) 内作 \(DC\) 的垂线\(Ox\)，连接 \(OP\)，

由于\(PD=PC\)，所以\(PO\perp DC\)，又因为平面 \(PDC\perp\)平面\(ABCD\)，所以\(PO\perp\)平面 \(ABCD\)，

所以 \(Ox\)、\(OP\) 、 \(OC\)两两垂直，以\(O\)为坐标原点，建立空间直角坐标系\(O-xyz\), 如图所示；

设 \(OP=a(a>0)\)，则\(O(0,0,0)\)， \(A(4,-3,0)\)，\(B(4,1,0)\)， \(C(0,1,0)\)， \(P(0,0, a)\)，

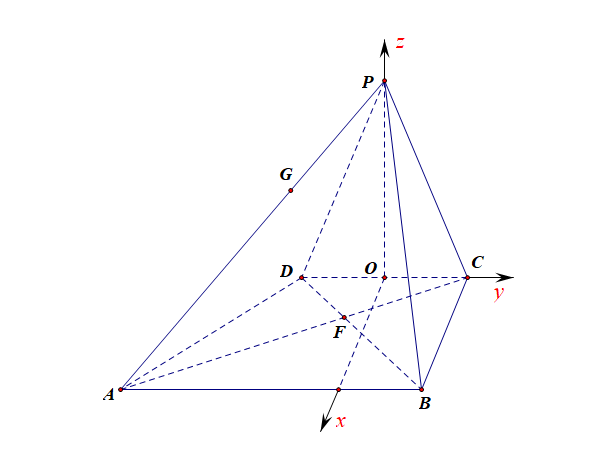
设平面 \(PAB\) 的法向量为\(\vec{m}=(x, y, z)\)，则 \(\vec{m}\perp \overrightarrow{BA}\)， \(\vec{m}\perp\overrightarrow{B P}\);

又\(\overrightarrow{BA}=(0,-4,0)\)，\(\overrightarrow{BP}=(-4,-1, a)\)，

所以\(\left\{\begin{array}{l}{4y=0}\\{-4x-y+az=0}\end{array}\right.\)，解得 \(y=0\), \(z=\cfrac{4}{a}x\)，

令\(x=a\)，则\(y=0\)，\(z=4\)，得 \(\vec{m}=(a, 0,4)\)

则cos \(<\vec{m},\vec{n}>=\cfrac{\vec{m}\cdot\vec{n}}{|\vec{m}|\times|\vec{n}|}=\cfrac{4}{\sqrt{a^{2}+16}}=\cfrac{\sqrt{2}}{2}\)，解得\(a^{2}=16\)，

由\(a>0\)， 则\(a=4\)， 所以点 \(P(0,0,4)\)，

所以\(\cos <\overrightarrow{PC}, \vec{m}>=\cfrac{-16}{\sqrt{17}\times\sqrt{16+16}}=-\cfrac{2\sqrt{34}}{17}\)

设\(PC\)与平面\(PAB\) 所成的角为 \(\theta\)，则\(\theta\in[0,\cfrac{\pi}{2}]\)，

所以\(\sin\theta=|\cos<\overrightarrow{PC},\vec{m}>|=\cfrac{2 \sqrt{34}}{17}\)，

即直线\(PC\)与平面 \(PAB\) 所成角的正弦值为\(\cfrac{2\sqrt{34}}{17}\)；

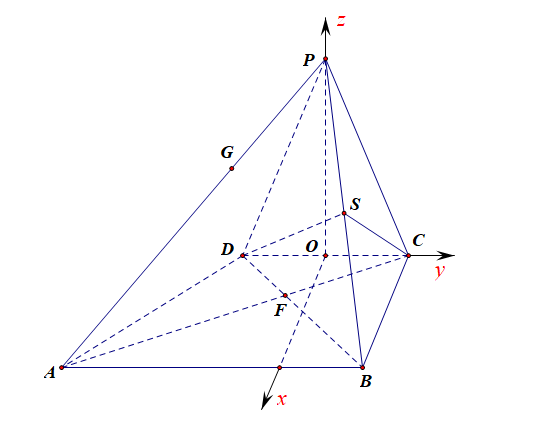
② 在棱 \(PB\) 上是否存在一点 \(S\)， 使得平面 \(SDC\perp\)平面\(PAB\)？若存在，求出 \(CS\) 的长度； 若不存在， 说明理由.

解析：假设存在满足条件的点 \(S\)，可设 \(\overrightarrow{PS}=\lambda\overrightarrow{PB}(0\leqslant\lambda\leqslant 1)\)，

则 \(\overrightarrow{CS}=\overrightarrow{CP}+\overrightarrow{PS}=\overrightarrow{CP}+\lambda\overrightarrow{PB}=(0,-1,4)+\lambda(4,1,-4)=(4\lambda,\lambda-1,4-4\lambda)\)

设平面\(SDC\)的法向量为 \(\vec{b}=(x, y, z)\)，则\(\vec{b}\perp\overrightarrow{DC}\)，\(\vec{b}\perp \overrightarrow{C S}\)，

又\(\overrightarrow{DC}=(0,4,0)\)，所以\(\left\{\begin{array}{l}{4y=0}\\{4\lambda x+(\lambda-1)y+(4-4\lambda)z=0}\end{array}\right.\)

解得\(y=0\)，\(\lambda x=(\lambda-1)z\)，

令\(z=\lambda\)，\(x=\lambda-1\)，则 \(\vec{b}=(\lambda-1,0,\lambda)\)，

由平面 \(SDC\perp\)平面 \(PAB\)， \(\vec{b}\perp \vec{m}\),

所以 \(4(\lambda-1)+4\lambda=0\)， 解得 \(\lambda=\cfrac{1}{2}\in[0,1]\)，

所以存在满足条件的\(S\)点，且\(S\)为\(PB\)的中点，此时 \(S\) 点坐标为\((2, \cfrac{1}{2}, 2)\)， 且\(CS=\sqrt{4+\cfrac{1}{4}+4}=\cfrac{\sqrt{33}}{2}\).