翻折问题

前言

一旦涉及翻折问题，平面问题往往就变化为空间问题，难度就立马提升了，此时需要我们好好观察和思考，翻折前后哪些量变化了，哪些量没有变化。

典例剖析

【北京人大附中高二】【2016浙江卷】如图，已知平面四边形\(ABCD\)， \(AB=BC=3\)，\(CD=1\)，\(AD\)\(=\)\(\sqrt{5}\)，\(\angle ADC=90^{\circ}\)，沿直线\(AC\)将\(\triangle ACD\) 翻折成 \(\triangle ACD'\)，则直线\(AC\) 与\(BD'\) 所成角的余弦的最大值为__________。

法1：几何法，通过作---证---算的步骤完成。

如图所示，取\(AC\)的中点\(O\)，由于\(AB=BC=3\)，故\(BO\perp AC\)，

在\(Rt\triangle ACD'\)中，\(AC=\sqrt{1^{2}+(\sqrt{5})^{2}}=\sqrt{6}\)，

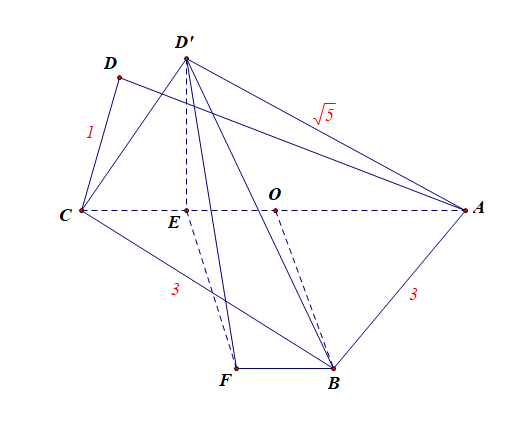
作 \(D'E\perp AC\)，垂足为\(E\)，\(D'E=\cfrac{1\times\sqrt{5}}{\sqrt{6}}=\cfrac{\sqrt{30}}{6}\)，

\(CO=\cfrac{\sqrt{6}}{2}\)，\(CE=\cfrac{DC^{2}}{CA}=\cfrac{1}{\sqrt{6}}=\cfrac{\sqrt{6}}{6}\)，故\(EO=CO-CE=\cfrac{\sqrt{6}}{3}\)，

过点\(B\)作\(BF//AC\)，过点\(E\)作\(EF//BO\)交\(BF\)于点\(F\)，则\(EF\perp AC\)，

连接\(D'F\)，\(\angle FBD'\)为异面直线\(AC\)与\(BD'\)所成的角求作异面直线所成的角，常用的方法是将其中的一条直线平移和另一条共面，此时这两条共面直线所成的角，即两异面直线所成的角。故两异面直线所成的角的范围为\((0,\cfrac{\pi}{2}]\)，此题目中，由于\(AC\)//\(BF\)，故\(\angle FBD'\)即异面直线\(AC\)与\(BD'\)所成的角，

则四边形\(BOEF\)为矩形，所以\(BF=EO=\cfrac{\sqrt{6}}{3}\)，

\(EF=BO=\sqrt{3^{2}-(\cfrac{\sqrt{6}}{2})^{2}}=\cfrac{\sqrt{30}}{2}\)，

则\(\angle FED'\)为二面角 \(D'-CA-B\)的平面角，设为\(\theta\)，

则\(D'F^{2}=(\cfrac{\sqrt{30}}{6})^{2}+(\cfrac{\sqrt{30}}{2})^{2}-2\times\cfrac{\sqrt{30}}{6}\times\cfrac{\sqrt{30}}{2}\times\cos\theta\)

\(=\cfrac{25}{3}-5\cos\theta \geqslant \cfrac{10}{3}\)，当\(\cos\theta=1\) 时取等号，

故\(BD'\)的最小值 \(BD'_{min}=\sqrt{\cfrac{10}{3}+(\cfrac{\sqrt{6}}{3})^{2}}=2\)，

故直线\(AC\)与\(BD'\)所成角\(\alpha\)的余弦在\(Rt\triangle BFD'\)中，\(\cos\)\(\alpha\)\(=\)\(\cfrac{邻}{斜}\)，由于邻边\(BF\)长度不变，故斜边\(BD'\)最小时，\(\cos\alpha\)的值最大；的最大值\([\cos\alpha]_{max}=\cfrac{BF}{BD'}=\cfrac{\frac{\sqrt{6}}{3}}{2}=\cfrac{\sqrt{6}}{6}\)

法2： 也可以考虑使用空间向量法；

【2018年全国卷Ⅰ第18题】如图，四边形\(ABCD\)为正方形，\(E\)，\(F\)分别为\(AD\)，\(BC\)的中点，以\(DF\)为折痕把\(\triangle DFC\)折起，使点\(C\)到达点\(P\)的位置，且\(PF\perp BF\)，

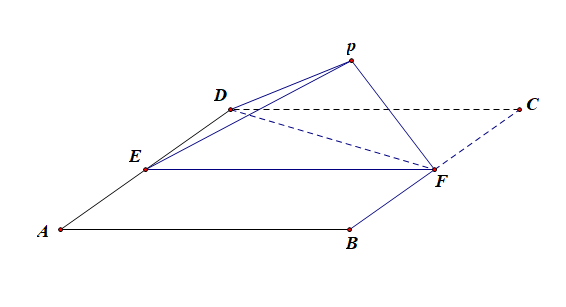
(1).证明：平面\(PEF\perp\)平面\(ABFD\)；

证明：由已知可得，\(BF\perp PF\)，\(BF\perp EF\)，

又\(PF\cap EF=F\)，\(PF\subseteq\)平面\(PEF\)，\(EF\subseteq\)平面\(PEF\)，

所以\(BF\perp\)平面\(PEF\)，又\(BF\subseteq\)平面\(ABFD\)，

所以平面\(PEF\perp\)平面\(ABFD\)；

(2).求\(DP\)与平面\(ABFD\)所成角的正弦值。

解：作\(PH\perp EF\)，垂足为\(H\)，由(1)得，\(PH\perp\)平面\(ABFD\)，以\(H\)为坐标原点，\(\overrightarrow{HF}\)的方向为\(y\)轴正方向，\(|\overrightarrow{BF}|\)为单位长，建立如图所示的空间直角坐标系\(H-xyz\)，

由(1)得到，\(DE\perp PE\)，又\(DP=2\)，\(DE=1\)，所以\(PE=\sqrt{3}\)，

又\(PF=1\)，\(EF=2\)，所以\(PE\perp PF\)，可得\(PH=\cfrac{\sqrt{3}}{2}\)，\(EH=\cfrac{3}{2}\)，

则\(H(0，0，0)\)，\(P(0，0，\cfrac{\sqrt{3}}{2})\)，\(D(-1，-\cfrac{3}{2}，0)\)，

则\(\overrightarrow{DP}=(1，\cfrac{3}{2}，\cfrac{\sqrt{3}}{2})\)，\(\overrightarrow{HP}=(0，0，\cfrac{\sqrt{3}}{2})\)为平面\(ABFD\)的法向量，

设\(DP\)与平面\(ABFD\)所成角为\(\theta\)，则\(sin\theta=|cos<\overrightarrow{HP}，\overrightarrow{DP}>|=|\cfrac{\overrightarrow{HP}\cdot \overrightarrow{DP}}{|\overrightarrow{HP}||\overrightarrow{DP}|}|=\cfrac{\frac{3}{4}}{\sqrt{3}}=\cfrac{\sqrt{3}}{4}\)，

所以\(DP\)与平面\(ABFD\)所成角的正弦值为\(\cfrac{\sqrt{3}}{4}\)。

如图所示, 已知长方形 \(ABCD\) 中， \(AB=2AD=2\sqrt{2}\)， \(M\) 为 \(DC\) 的中点， 将 \(\triangle\)\(ADM\) 沿 \(AM\) 折起， 使得 \(AD\)\(\perp\)\(BM\).

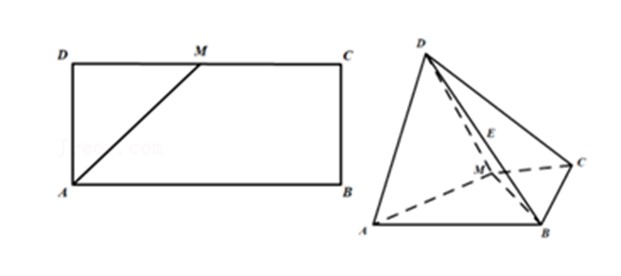
(1). 求证: 平面 \(ADM\perp\) 平面 \(ABCM\)；

证明: 由于长方形 \(ABCD\) 中， \(AB=2AD=2\sqrt{2}\)， \(M\) 为 \(DC\) 的中点，

所以 \(AM=BM=2\)， \(AM^{2}+BM^{2}=AB^{2}\)， 则 \(BM\perp AM\)，

又 \(AD\perp BM\)， \(AD\bigcap AM=A\)，所以 \(BM\perp\) 平面 \(ADM\)，

又 \(BM\subset\) 平面 \(ABCM\)， 平面 \(ADM\perp\) 平面 \(ABCM\)；

(2). 若 \(E\) 点在线段 \(BD\) 上， 且满足 \(BE=\cfrac{2}{3}BD\)， 求三棱雉 \(E-ABM\) 的体积.

解：取 \(A M\) 的中点 \(F\)， 连接 \(DF\)，

由于\(AB=2AD=2\sqrt{2}\)， \(M\) 为 \(DC\) 的中点， 所以\(AD=DM=\sqrt{2}\)，

所以 \(DF\perp AM\)， 得 \(DF=1\)，

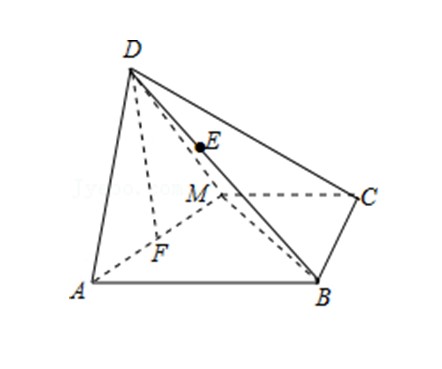
由（1）知， 平面 \(ADM\perp\) 平面 \(ABCM\)， \(DF\subset\) 平面 \(ADM\)， 平面 \(ADM\cap\) 平面 \(ABCM=AM\)，

所以 \(DF\perp\) 平面 \(ABCM\)，

由于 \(\overrightarrow{BE}=\cfrac{2}{3}\overrightarrow{BD}\)， \(E\) 到平面 \(ABCM\) 的距离等于 \(D\) 到平面 \(ABCM\) 的距离的 \(\cfrac{2}{3}\)，

所以，\(V_{E-ABM}=\cfrac{2}{3}V_{D-ABM}=\cfrac{2}{3}\times\cfrac{1}{3}S_{\Delta ABM}\cdot DF\)

\(=\cfrac{2}{3}\times\cfrac{1}{3}\times\cfrac{1}{2}\times 2\times 2\times 1=\cfrac{4}{9}\) .