快速高效地做三角函数图像

前言

分类说明

求函数的值域问题时，可以用\(\omega x+\phi\)作为横轴，快速做图像来计算；此时比用\(x\)轴做图像计算快的多；

求函数\(y=2sin(2x+\cfrac{\pi}{6})+1，x\in[0，\cfrac{\pi}{2}]\)的值域。

法1：横轴为\(x\)，如图1所示，利用图像的变换得到函数\(y=2sin(2x+\cfrac{\pi}{6})+1，x\in[0，\cfrac{\pi}{2}]\)的图像，

由图像可以看出来，当\(x=\cfrac{\pi}{2}\)时，函数\(f(x)_{min}=2sin(2\times\cfrac{\pi}{2}+\cfrac{\pi}{6})+1=0\)，

当\(x=\cfrac{\pi}{6}\)时，函数\(f(x)_{max}=2sin(2\times\cfrac{\pi}{6}+\cfrac{\pi}{6})+1=3\)，

故函数的值域为\([0，3]\)。

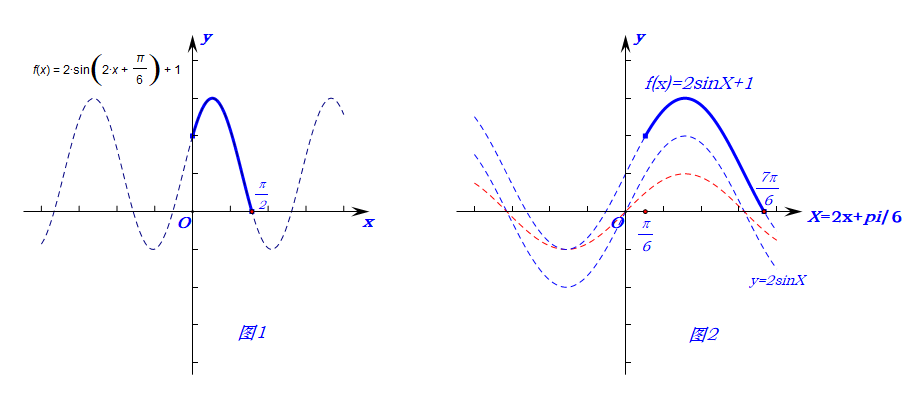
法2，整体代换，如图2所示，横轴为\(2x+\cfrac{\pi}{6}=X\)，由\(0\leq x\leq \cfrac{\pi}{2}\)，

故\(\cfrac{\pi}{6}\leq 2x+\cfrac{\pi}{6}\leq \cfrac{7\pi}{6}\)，则\(-\cfrac{1}{2}\leq sin(2x+\cfrac{\pi}{6})\leq 1\)，

则\(0\leq 2sin(2x+\cfrac{\pi}{6})+1\leq 3\)，故\(0\leq y\leq 3\)。

反思总结：

1、从作图角度讲，图2的做法由于使用了整体代换，作图过程简单明了，思路清晰，截取快捷，故常用图2的方法来做三角函数的图像。

2、用图2的方法也可以求解函数的单调区间。比如，对函数\(y=2sinX+1\)而言，在\(X\in [\cfrac{\pi}{6}，\cfrac{\pi}{2}]\)上单调递增，即\(2x+\cfrac{\pi}{6}\in [\cfrac{\pi}{6}，\cfrac{\pi}{2}]\)上单调递增，解得\(x\in [0，\cfrac{\pi}{6}]\)，即函数\(y=2sin(2x+\cfrac{\pi}{6})+1\)在区间\([0，\cfrac{\pi}{6}]\)上单调递增，和图1的单调递增区间是一样的。

求限定区间上的三角函数的单调性；

【2016\(\cdot\)天津高考】已知函数\(f(x)=4tanx\cdot sin(\cfrac{\pi}{2}-x)\cdot cos(x-\cfrac{\pi}{3})-\sqrt{3}\)，

(1).求函数的定义域；

分析：由函数解析式可知，需要让\(tanx\)有意义，故定义域为\(\{x\mid x\neq k\pi+\cfrac{\pi}{2}，k\in Z\}\)

(2).试讨论\(f(x)\)在区间\([-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)上的单调性。

分析：先将所给函数化简为正弦型或者余弦型，

\(f(x)=4tanx\cdot cosx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}\)

\(=4sinx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}\)

\(=2sinxcosx+2\sqrt{3}sin^2x-\sqrt{3}\)

\(=sin2x+\sqrt{3}(1-cos2x)-\sqrt{3}\)

\(=sin2x-\sqrt{3}cos2x\)

\(=2sin(2x-\cfrac{\pi}{3})\)

法1：先求解函数在\(x\in R\)上的单调区间，

令\(2k\pi-\cfrac{\pi}{2}< 2x-\cfrac{\pi}{3}< 2k\pi+\cfrac{\pi}{2}(k\in Z)\)，

得到单调递增区间为\((k\pi-\cfrac{\pi}{12}，k\pi+\cfrac{5\pi}{12})(k\in Z)\)，

然后给\(k\)赋值，令\(k=0\)，又因为\(x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)，

[说明：求得的单调递增区间和给定区间求交集，即为所求的单调递增区间；剩余的即为单调递减区间]

得到函数在区间\((-\cfrac{\pi}{12}，\cfrac{\pi}{4}]\)上单调递增，在区间\([-\cfrac{\pi}{4}，-\cfrac{\pi}{12})\)上单调递减。

法2：由\(-\cfrac{\pi}{4}\leq x\leq \cfrac{\pi}{4}\)，求得\(-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}\)，结合横轴为\(2x-\cfrac{\pi}{3}\)的图像可知，

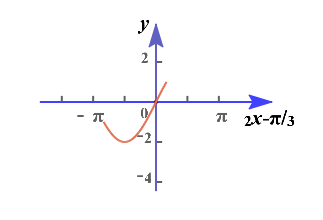
当\(-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}< -\cfrac{\pi}{2}\)时，求得函数在区间\([-\cfrac{\pi}{4}，-\cfrac{\pi}{12})\)单调递减；

当\(-\cfrac{\pi}{2}< 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}\)时，求得函数在区间\((-\cfrac{\pi}{12}，\cfrac{\pi}{4}]\)单调递增；

导函数中含有三角函数且\(\omega=1\)时，尽可能以\(x\)为横轴，快速作图并平移；若\(\omega\neq 1\)时，仿上例完成即可；

【2020届高三模拟训练】若关于\(x\)的方程\(\cfrac{me^x}{2}-\sin x=0\)在\([-\pi,-\cfrac{\pi}{2}]\)上有\(2\)个零点，则实数\(m\)的取值范围是【】

$A.(-\sqrt{2}e^{\frac{3\pi}{4}}，0)$ $B.(-\sqrt{2}e^{\frac{\pi}{4}}，-2e^{\frac{\pi}{2}}]$ $C.(-\sqrt{2}e^{\frac{3\pi}{4}}，-2e^{\frac{\pi}{2}}]$ $D.(-\sqrt{2}e^{\frac{3\pi}{4}}，-2e^{\frac{\pi}{2}})$

分析：由于\(\cfrac{me^x}{2}-\sin x=0\)，故\(m=\cfrac{2\sin x}{e^x}\)，令\(f(x)=\cfrac{2\sin x}{e^x}\)，则\(f'(x)=\cfrac{2\sqrt{2}\cos(x+\cfrac{\pi}{4})}{e^x}\)，

接下来可以从数的角度，通过解\(f'(x)>0\)和\(f'(x)<0\)求得单调区间，此处从略；

也可以从形的角度直接解读单调区间，以下重点说明如何从形的角度直接解读单调区间；

由于\(e^x>0\)，故主要借助函数\(y=\cos(x+\cfrac{\pi}{4})\)，\(x\in [-\pi,-\cfrac{\pi}{2}]\)，

可以先做出\(y=\cos x\)的图像，再通过平移得到\(y=\cos(x+\cfrac{\pi}{4})\)，\(x\in [-\pi,-\cfrac{\pi}{2}]\)的图像，

可知当\(x\in [-\pi,-\cfrac{3\pi}{4})\)，\(f'(x)<0\)，当\(x\in (-\cfrac{3\pi}{4}，-\cfrac{\pi}{2}]\)时，\(f'(x)>0\)，

故函数\(f(x)\)在区间\([-\pi,-\cfrac{3\pi}{4})\)单调递减，在区间\(x\in (-\cfrac{3\pi}{4}，-\cfrac{\pi}{2}]\)单调递增，

又\(f(-\pi)=0\)，\(f(-\cfrac{3\pi}{4})=-\sqrt{2}e^{\frac{3\pi}{4}}\)，\(f(-\cfrac{\pi}{2})=-2e^{\frac{\pi}{2}}\)，

做出函数的大致图像，由图像可知，\(y=m\)和\(y=f(x)\)的图像要有两个交点，

则\(m\in (-\sqrt{2}e^{\frac{3\pi}{4}}，-2e^{\frac{\pi}{2}}]\)，故选\(C\)；

以下常见的三角函数的图像，希望大家熟练掌握；

①依托函数\(f(x)=\sin x\)的图像，用五点法作函数\(g(x)=\sin(x\pm\cfrac{\pi}{4})\)[以及\(\pm \cfrac{\pi}{6}\)和\(\pm \cfrac{\pi}{3}\)]的图像；

②依托函数\(f(x)=\cos x\)的图像，用五点法作函数\(g(x)=\cos(x\pm\cfrac{\pi}{4})\)[以及\(\pm \cfrac{\pi}{6}\)和\(\pm \cfrac{\pi}{3}\)]的图像；

③\(y=2\sin(2x+\cfrac{\pi}{3})+1\)的图像在一个周期上的图像；

④\(y=2\sin(2x+\cfrac{\pi}{3})+1\)的图像在限定周期 \([0,\pi]\) 上的图像；

⑤学会以\(2x+\cfrac{\pi}{3}\)为横轴，作函数\(y=2\sin(2x+\cfrac{\pi}{3})\)的图像；