探究|几何体的体积比

前言

思考探究

[案例1]如图，三棱柱\(ABC-A_1B_1C_1\)中，若\(E\)、\(F\)分别是\(AB\)，\(AC\)的中点，平面\(EB_1C_1\)将三棱柱分成体积为\(V_1\)，\(V_2\)的两部分，求\(V_1：V_2\)的值。

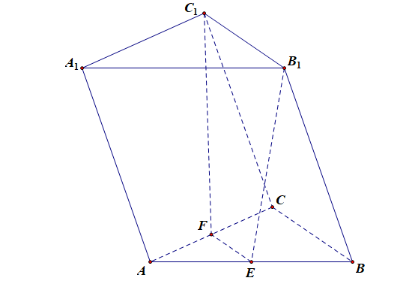
分析1：如下图所示，连结\(B_1F\)，\(B_1C\)，为便于分析和求解，令三棱台\(AEF-A_1B_1C_1\)的体积\(V_1\)，不规则几何体的体积\(V_{B_1C_1-BCFE}=V_2\)，令三棱柱\(ABC-A_1B_1C_1\)的高为\(h\)，\(S_{\triangle AEF}=s\)，则\(S_{\triangle ABC}\)\(=S_{\triangle A_1B_1C_1}\)\(=4s\)，

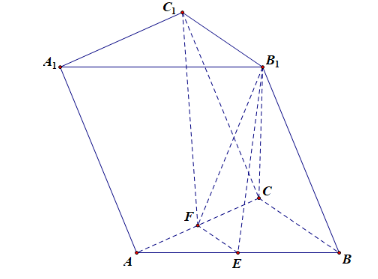
则三棱台\(AEF-A_1B_1C_1\)的体积\(V_1=\cfrac{1}{3}(S_{上}+S_{下}+\sqrt{S_{上}S_{下}})h\)可求解，接下来关键是求解\(V_{BC-B_1C_1FE}\)\(=V_2\)，此时可以分割为四棱锥\(B_1-BCFE\)和三棱锥\(B_1-CC_1F\)来考虑求解，而四棱锥的体积\(V_{B_1-BCFE}\)可容易求解，就是三棱锥的体积\(V_{B_1-CC_1F}\)不能有效利用现有的假设条件，造成比值的约分效果，故此思路基本停滞，需要考虑更换思路。

分析2：接上思考，\(V_1\)可以表达，那么利用现有条件，能不能表达三棱柱的体积\(V_{ABC-A_1B_1C_1}\)，我们发现，这是很容易的，故虽然不能通过组合加的思路求解\(V_2\)，但是可以通过相减的思路求得\(V_2\)，故思路打通，可以考虑组织书写。

求解：如下图所示，为便于分析和求解，令三棱柱\(ABC-A_1B_1C_1\)的体积为\(V\)，三棱台\(AEF-A_1B_1C_1\)的体积为\(V_1\)，不规则几何体的体积为\(V_{B_1C_1-BCFE}=V_2\)，令三棱柱\(ABC-A_1B_1C_1\)的高为\(h\)，\(S_{\triangle AEF}=s\)，则\(S_{\triangle ABC}=S_{\triangle A_1B_1C_1}=4s\)，

则由三棱台的体积公式\(V_{棱台}=\cfrac{1}{3}(S_{上}+S_{下}+\sqrt{S_{上}S_{下}})h\)可知，

\(V_1=V_{AEF-A_1B_1C_1}=\cfrac{1}{3}(s+4s+\sqrt{s\cdot 4s})h=\cfrac{7}{3}sh\)，

由三棱柱的体积公式\(V_{棱柱}=S\cdot h\)可知，\(V_{ABC-A_1B_1C_1}=V=S\cdot h=4sh\)，

则\(V_2=V_{B_1C_1-BCFE}=V-V_1=4sh-\cfrac{7}{3}sh=\cfrac{5}{3}sh\)，

故\(\cfrac{V_1}{V_2}=\cfrac{\frac{7}{3}sh}{\frac{5}{3}sh}=\cfrac{7}{5}\)；

解后反思

①熟练记忆各种常用且常见的几何体的体积公式；

②几何体的常用拆分和常用组合；

③加减运算是同一级的，通过加运算不能完成的，能否掉头思考通过减运算来完成；

数学美感

【一级运算和二级运算之间的相互转化】

①[加法变减法]斜率公式\(k=\cfrac{y_2-y_1}{x_2-x_1}\)，那么遇到\(\cfrac{y+3}{x+2}\)，就可以联系\(\cfrac{y+3}{x+2}=\cfrac{y-(-3)}{x-(-2)}\)，

故该表达式可以理解为定点\((-2,-3)\)与动点\((x,y)\)连线的斜率，这样数形结合就完成了；

②[乘法变除法]椭圆\(\cfrac{x^2}{a^2}+\cfrac{x^2}{b^2}=1(a>b>0)\)，那么遇到\(3x^2+4y^2=1\)，就可以改写为\(\cfrac{x^2}{\frac{1}{3}}+\cfrac{y^2}{\frac{1}{4}}=1\)，

【向量的模的运算】已知\(|\vec{a}|=1，|\vec{b}|=2，<\vec{a}，\vec{b}>=60^{\circ}\)，求\(|\vec{a}+2\vec{b}|\)

法1：基向量法，以退为进法；

\(|\vec{a}+2\vec{b}|^2=\vec{a}^2+4\vec{b}^2+2\times 2\times \vec{a}\cdot \vec{b}\)；

\(=|\vec{a}|^2+4|\vec{b}|^2+4|\vec{a}|\cdot |\vec{b}|\cdot cos60^{\circ}\)；

\(=1+16+4\times 1\times 2\times cos60^{\circ}=21\)，

故\(|\vec{a}+2\vec{b}|=\sqrt{21}\)。

【代数式求值】已知\(x+x^{-1}=3\)，求\(x^{\frac{1}{2}}+x^{-\frac{1}{2}}=\sqrt{(x^{\frac{1}{2}}+x^{-\frac{1}{2}})^2}=\sqrt{5}\)

【对数的运算】求值：\(log_2^\;{(\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}})}\)

\(log_2^\;{(\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}})}\)

\(=\cfrac{1}{2}\cdot 2 log_2^\;{(\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}})}\)

\(=\cfrac{1}{2}log_2^\;{(\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}})^2}\)

\(=\cfrac{1}{2}\)

【对数的运算】求值：\(5^{lg30}\cdot (\cfrac{1}{3})^{lg0.5}\)

分析：设\(5^{lg30}\cdot (\cfrac{1}{3})^{lg0.5}=x\)，两边同时取对数，

得到\(lgx=lg[5^{lg30}\cdot (\cfrac{1}{3})^{lg0.5}]\)，

即\(lgx=lg30\cdot lg5+lg0.5\cdot lg\cfrac{1}{3}\)

即\(lgx =(lg3+1)\cdot lg5+(-lg2)\cdot (-lg3)\)

即\(lgx=lg3\cdot lg5+lg5+lg2\cdot lg3\)

即\(lgx=lg3(lg2+lg5)+lg5\)

即\(lgx=lg3+lg5=lg15\)，

即\(x=15\)；

【同思路】求\(a^{lnb}\)的最值，令\(a^{lnb}=t\)，则\(lnt=lnb\cdot lna\)；

【三角函数求值】已知\(\alpha\)为第二象限角，且\(sin2\alpha=-\cfrac{24}{25}\)，求\(cos\alpha-sin\alpha\)的值。

分析：\(|cos\alpha-sin\alpha|=\sqrt{(cos\alpha-sin\alpha)^2}=\sqrt{1-sin2\alpha}=\sqrt{1-(-\cfrac{24}{25})}=\cfrac{7}{5}\)，

又由于\(\alpha\)为第二象限角可知，\(cos\alpha<0，sin\alpha>0\)，故\(cos\alpha-sin\alpha=-\cfrac{7}{5}\)。

【不等式大小比较】比较大小：\(P=\sqrt{6}+\sqrt{7}\)与\(Q=\sqrt{5}+\sqrt{8}\)

分析：先平方，再开方。\(P^2=6+7+2\sqrt{42}\)；\(Q^2=5+8+2\sqrt{40}\)；

由于\(P^2>Q^2\)，\(P>0\)，\(Q>0\)，故\(P>Q\)

【三角函数式的化简+二倍角的正弦多次逆用】化简求值：\(cos20^{\circ}\cdot cos40^{\circ}\cdot cos60^{\circ}\cdot cos80^{\circ}\)

分析：原式=\(\cfrac{1}{2}\cdot \cfrac{2sin20^{\circ}\cdot cos20^{\circ}\cdot cos40^{\circ}\cdot cos80^{\circ}}{2sin20^{\circ}}\)

\(=\cfrac{1}{2}\cdot \cfrac{sin40^{\circ}\cdot cos40^{\circ}\cdot cos80^{\circ}}{2sin20^{\circ}}\)

\(=\cfrac{1}{2}\cdot \cfrac{2\cdot sin40^{\circ}\cdot cos40^{\circ}\cdot cos80^{\circ}}{2\cdot 2sin20^{\circ}}\)

\(=\cfrac{1}{2}\cdot \cfrac{sin80^{\circ}\cdot cos80^{\circ}}{4sin20^{\circ}}\)

\(=\cfrac{1}{2}\cdot \cfrac{sin160^{\circ}}{8sin20^{\circ}}\)

\(=\cfrac{1}{2}\cdot \cfrac{1}{8}= \cfrac{1}{16}\)。

【2019届高三理科数学第三轮模拟训练题】有一块池塘的荷叶生长速度每天是前一天的一倍，已知第\(20\)天时，荷叶刚好盖满池塘，问多少天荷叶刚好盖住池塘的一半？

思路一：我们一般是转化为等比数列求解，这是常规的思路，也是很费时间的思路。

思路二：我们以退为进，由于每天的荷叶生长速度每天是前一天的一倍，第\(20\)天时，荷叶刚好盖满池塘，那么第\(20-1=19\)天时，必然刚好盖住池塘的一半。

【同类型】三角形数阵的下一行的第一个，与上一行的最后一个。

相关公式推导

体积公式推导：特殊到一般，祖暅原理；

正方体，六面体，棱柱，棱锥，棱台

面积公式推导：