人教版|反三角函数

前言

三角函数是研究以实数[或者以角为自变量，角与实数之间是一一对应的]为自变量，以函数值为因变量的映射，简单说就是角到实数的映射；反三角函数是研究以实数为自变量，以函数值[或者以角为因变量]为因变量的映射，简单说就是实数到角的映射；同名的三角函数和反三角函数之间是互为反函数的；

正弦与反正弦

\(f(x)=\arcsin x\)的性质列举：

①定义域为\([-1,1]\)；值域为\([-\cfrac{\pi}{2},\cfrac{\pi}{2}]\);

②在\([-1,1]\)上单调递增；③奇函数；④关于点\((0,0)\)对称；

⑤其图像与\(y=\sin x,x\in[-\cfrac{\pi}{2},\cfrac{\pi}{2}]\)的图像关于\(y=x\)对称；

余弦与反余弦

\(g(x)=\arccos x\)的性质列举：

①定义域为\([-1,1]\)；值域为\([0,\pi]\);

②在\([-1,1]\)上单调递减；③非奇非偶函数；④关于点\((0,\cfrac{\pi}{2})\)对称；

⑤其图像与\(y=\cos x,x\in[0,\pi]\)的图像关于\(y=x\)对称；

正切与反正切

\(h(x)=\arctan x\)的性质列举：

①定义域为\((-\infty,+\infty)\)；值域为\((-\cfrac{\pi}{2},\cfrac{\pi}{2})\);

②在\((-\infty,+\infty)\)上单调递增；③奇函数；④关于点\((0,0)\)对称；

⑤其图像与\(y=\tan x,x\in(-\cfrac{\pi}{2},\cfrac{\pi}{2})\)的图像关于\(y=x\)对称；

典例剖析

【2020北京人大附中高一试题】\(\arcsin(\sin\cfrac{2\pi}{3})\)=_____________.

分析：\(\arcsin(\sin\cfrac{2\pi}{3})=\arcsin(\cfrac{\sqrt{3}}{2})=\cfrac{\pi}{3}\)；

【2020北京人大附中高一试题】\(\arcsin(-\cfrac{1}{2})+\arccos(-\cfrac{\sqrt{3}}{2})+\arcsin(-\sqrt{3})\)

分析：\(\arcsin(-\cfrac{1}{2})+\arccos(-\cfrac{\sqrt{3}}{2})+\arcsin(-\sqrt{3})\)

\(=-\cfrac{\pi}{6}+\cfrac{5\pi}{6}-\cfrac{\pi}{3}=\cfrac{\pi}{3}\)

【2020北京人大附中高一试题】\(\cfrac{\arcsin\frac{\sqrt{3}}{2}-\arccos(-\frac{1}{2})}{\arctan(-\sqrt{3})}\)

分析：\(\cfrac{\arcsin\frac{\sqrt{3}}{2}-\arccos(-\frac{1}{2})}{\arctan(-\sqrt{3})}\)

\(=\cfrac{\frac{\pi}{3}-\frac{2\pi}{3}}{-\frac{\pi}{3}}=1\)

【2020北京人大附中高一试题】已知直线倾斜角\(\theta\)的范围是\([0,\pi)\)，当\(\theta\neq \cfrac{\pi}{2}\)时，\(\tan\theta\)等于直线的斜率值；则直线\(x+2y+1=0\)的倾斜角为【】

$A.\arcsin(-\cfrac{\sqrt{5}}{5})$ $B.\arccos(-\cfrac{2\sqrt{5}}{5})$ $C.\arctan(-\cfrac{1}{2})$ $D.-\arctan(\cfrac{1}{2})$

分析：由题可知，直线的斜率\(k=\tan\theta=-\cfrac{1}{2}\)，倾斜角为钝角；

引入非零比例因子，可得到\(\sin\theta=m\)，\(\cos\theta=-2m\)，由于\(\theta\in [0,\pi)\)，故\(m>0\)，

由\(m^2+(-2m)^2=1\)，得到\(m=\cfrac{\sqrt{5}}{5}\)，

故有\(\sin\theta=\cfrac{\sqrt{5}}{5}\)，\(\cos\theta=-\cfrac{2\sqrt{5}}{5}\)，\(\tan\theta=-\cfrac{1}{2}\)，

若用反正弦刻画倾斜角，则\(\theta=\pi-\arcsin(\cfrac{\sqrt{5}}{5})\)，故\(A\)错误；

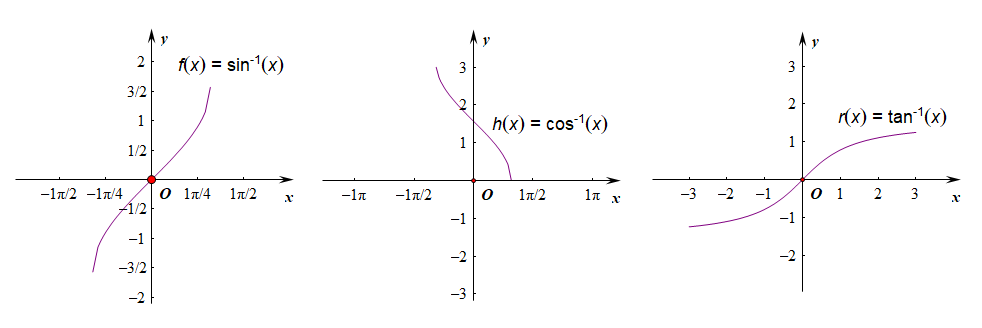
若用反余弦刻画倾斜角，则\(\theta=\arccos(-\cfrac{2\sqrt{5}}{5})\)，故\(B\)正确；

若用反正切刻画倾斜角，则\(\theta=\pi-\arctan(\cfrac{1}{2})\)，故\(C\)、\(D\)错误；

解后反思：①由于\(f(x)=\arcsin x\)为奇函数，故\(\arcsin(-\cfrac{\sqrt{5}}{5})=-\arcsin(\cfrac{\sqrt{5}}{5})\)为负角；

由于\(f(x)=\arctan x\)为奇函数，故\(\arctan(-\cfrac{1}{2})=-\arctan(\cfrac{1}{2})\)为负角；

②\(\arctan(-\cfrac{1}{2})=-\arctan(\cfrac{1}{2})\)，但是\(\arctan(-\cfrac{1}{2})\neq \pi-\arctan(\cfrac{1}{2})\)

【2020北京人大附中高一向量部分选做题】求证：在区间\((0,\cfrac{\pi}{2})\)内存在唯一的实数对\((c,d)\)，\(c,d\in(0,\cfrac{\pi}{2})\)，且\(c<d\)，使得\(\sin(\cos c)=c\)，\(\cos(\sin d)=d\)成立。