2020届陕西省质检数学典例[1-3]解析
![2020届陕西省质检数学典例[1-3]解析](https://images.cnblogs.com/cnblogs_com/wanghai0666/1784871/o_20080714323319735190_16.jpg)
2020届陕西省质检数学典例[1-3]解析
前言
一检典例
分析：通过分析题意，得到函数\(g(x)\)的解析式为\(g(x)=\left\{\begin{array}{l}{(1-2a)x+1，x<2}\\{log_a(x-1)，x\geqslant 2}\end{array}\right.\quad\)
则由函数\(g(x)\)在\((-\infty，+\infty)\)上是减函数，
得到\(\left\{\begin{array}{l}{1-2a<0}\\{0<a<1}\\{(1-2a)\cdot 2+1\geqslant log_a(2-1)}\end{array}\right.\)，解得\(a\in (\cfrac{1}{2},\cfrac{3}{4}]\)，故选\(C\).
法1：如图所示，由双曲线的定义可知，\(|MF_1|-|MF_2|=2a\)，即\(|MF_1|=|MF_2|+2a\)，
故\(\cfrac{|MF_1|-2a}{|MF_1|^2}=\cfrac{|MF_2|+2a-2a}{(|MF_2|+2a)^2}=\cfrac{|MF_2|}{(|MF_2|+2a)^2}=\cfrac{|MF_2|}{|MF_2|^2+4a|MF_2|+4a^2}\)
\(=\cfrac{1}{|MF_2|+\frac{4a^2}{|MF_2|}+4a}\leqslant \cfrac{1}{2\sqrt{4a^2}+4a}=\cfrac{1}{8a}=\cfrac{1}{4}\)，当且仅当\(|MF_2|=2a\)时取到等号；
故解得\(a=\cfrac{1}{2}\)，结合题意\(|A_1A_2|\geqslant |A_2F_2|\)，
即\(2a\geqslant c-a\)，则\(3a\geqslant c\)，即\(\cfrac{c}{a}\leqslant 3\)，
又由于双曲线的离心率\(e=\cfrac{c}{a}>1\)，故\(1<\cfrac{c}{a}\leqslant 3\)，
则\(\cfrac{1}{2}=a<c\leqslant 3a=\cfrac{3}{2}\)，故\(1<2c\leqslant 3\)，故选\(D\)。
解后反思：①牢记双曲线的定义的使用；②分式形式的化简变形技巧；③离心率的范围的使用；④不等式性质的使用；⑤本题目还可以求解离心率的范围；
法2：由于\(|A_1A_2|\geqslant |A_2F_2|\)，即\(2a\geqslant c-a\)，
则\(3a\geqslant c\)，即\(\cfrac{c}{a}\leqslant 3\)，又由于双曲线的离心率\(e=\cfrac{c}{a}>1\)，
故\(1<\cfrac{c}{a}\leqslant 3\)，设\(|MF_1|=r\)，
则\(\cfrac{|MF_1|-2a}{|MF_1|^2}=\cfrac{r-2a}{r^2}=\cfrac{1}{r}-2a\cdot (\cfrac{1}{r})^2=-2a(\cfrac{1}{r}-\cfrac{1}{4a})^2+\cfrac{1}{8a}\leqslant \cfrac{1}{4}\)
当且仅当\(|MF_1|=4a\)时取到等号；故\(a=\cfrac{1}{2}\)，
则由\(1<\cfrac{c}{a}\leqslant 3\)得到，\(\cfrac{1}{2}=a<c\leqslant 3a=\cfrac{3}{2}\)，
故\(1<2c\leqslant 3\)，故选\(D\)。
法1：快捷解法，特殊化策略，[当我们做出适合题意的大致图像时，先想一想这样的图像是固定不变的，还是可以随着某一个量(比如随直线的斜率)动态变化的，如果是动态图像，那么先朝最特殊的情形靠拢，由于最特殊则思维、计算等必然是最简单的。]
当焦点弦\(MN\)特殊化为通经时，也是满足题意的，此时\(\triangle MON\sim \triangle POQ\)，则\(S_{\triangle MON}:S_{\triangle POQ}=(\cfrac{|OF|}{4})^2=\cfrac{1}{16}\)，故选\(D\)；
法2：当直线\(l\)垂直于\(x\)轴时，\(\triangle MON\sim \triangle POQ\)，则\(S_{\triangle MON}:S_{\triangle POQ}=(\cfrac{|OF|}{4})^2=\cfrac{1}{16}\)；
当直线\(l\)不垂直于\(x\)轴时，设直线\(l\)的方程为\(y=k(x+1)\)，设\(M(x_1,y_1)\)，\(N(x_2,y_2)\)，\(P(4,y_P)\)，\(Q(4,y_Q)\)，
联立\(\left\{\begin{array}{l}{y=k(x+1)}\\{y^2=-4x}\end{array}\right.\)，消去\(y\)得到\(k^2x^2+(2k^2+4)x+k^2=0\)，
则\(\Delta=(2k^2+4)^2-4k^4>0\)，且\(x_1x_2=\cfrac{k^2}{k^2}=1\)，
则\(S_{\triangle MON}:S_{\triangle POQ}=\cfrac{\frac{1}{2}\cdot |MO|\cdot|NO|\cdot \sin\angle MON}{\frac{1}{2}\cdot |PO|\cdot|QO|\cdot \sin\angle POQ}\)
\(=\cfrac{|MO|}{|PO|}\cdot \cfrac{|NO|}{|QO|}=\cfrac{|x_1|}{4}\cdot \cfrac{|x_2|}{4}=\cfrac{1}{16}\)；
综上可知，\(S_{\triangle MON}:S_{\triangle POQ}=\cfrac{1}{16}\)；故选\(D\)；
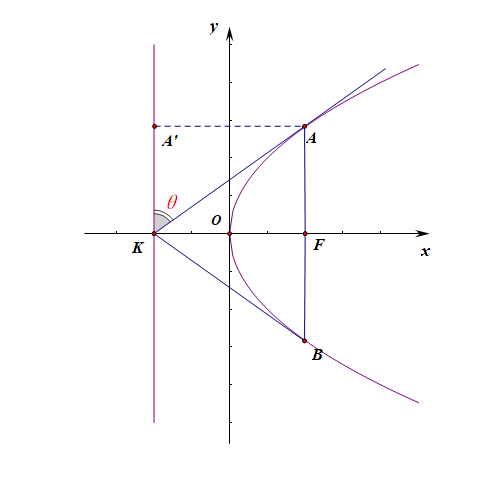
法1：由题目容易知道点\(K(-1,0)\)，点\(F(1,0)\)，[为了利用抛物线的定义，如下作图]
过点\(A\)做准线的垂线，垂足记为\(A'\)，则由抛物线的定义可知，\(|AA'|=|AF|\)，
故\(\cfrac{|AF|}{|AK|}\)最小，即需要\(\cfrac{|AA'|}{|AK|}\)最小，在\(Rt\triangle AA'K\)中，\(\cfrac{|AA'|}{|AK|}=sin\theta\)，
而当\(sin\theta\)最小时，即\(\theta\)最小时，直线\(AK\)和抛物线\(y^2=4x\)的位置状态是相切的。
设直线\(AK\)的斜率是\(k\)，则直线\(AK\)为\(y=k(x+1)\)，联立\(y^2=4x\)，
消去\(x\)，得到\(ky^2-4y+4k=0\)①，则其\(\Delta=16-4\times k\times 4k=0\)，解得\(k=1\)，舍去\(k=-1\)，
带入①式，得到\(y=2\)，代入\(y^2=4x\)，得到\(x=1\)，即切点\(A\)的坐标为\((1,2)\)，又由于\(F(1,0)\)，
故可知此时\(AB\perp x\)轴，且容易知道\(|AF|=|KF|=2\)，则\(|AK|=2\sqrt{2}=|BK|\)，
则\(|AK|+|BK|=4\sqrt{2}\)，故选\(D\).
解后反思：本题目中的题眼是，当\(sin\theta\)最小时，即\(\theta\)最小时，直线\(AK\)和抛物线\(y^2=4x\)的位置状态是相切的。
法2：[不利用抛物线定义，直接从函数的角度求解最小值，此时需要注意:抛物线\(y^2=4x\)上任意一点的坐标的设置技巧\((4t^2,4t)\)]
设抛物线\(y^2=4x\)上任意一点\(A\)的坐标\(A(4t^2,4t)\)，则由点\(K(-1,0)\)，点\(F(1,0)\)，
则要求\(\cfrac{|AF|}{|AK|}\)的最小值，为了计算方便，等价转化为求\(\cfrac{|AF|^2}{|AK|^2}\)的最小值，
\(\cfrac{|AF|^2}{|AK|^2}=\cfrac{(4t^2-1)^2+(4t)^2}{(4t^2+1)^2+(4t)^2}=\cfrac{16t^4-8t^2+1+16t^2}{16t^4+8t^2+1+16t^2}\)
\(=\cfrac{16t^4+8t^2+1}{16t^4+24t^2+1}==\cfrac{16t^4+24t^2+1-16t^2}{16t^4+24t^2+1}\)
\(=1-\cfrac{16t^2}{16t^4+24t^2+1}=1-\cfrac{16}{16t^2+\cfrac{1}{t^2}+24}\)
\(\geqslant 1-\cfrac{16}{2\sqrt{16t^2\cdot \frac{1}{t^2}}+24}=\cfrac{1}{2}\)
当且仅当\(16t^2=\cfrac{1}{t^2}\)时，即\(t=\cfrac{1}{2}\)时取到等号；
此时得到点\(A(1,2)\)，故图像特殊化为\(|AB|\) 成为通经，
故可知此时\(AB\perp x\)轴，且容易知道\(|AF|=|KF|=2\)，则\(|AK|=2\sqrt{2}=|BK|\)，
则\(|AK|+|BK|=4\sqrt{2}\)，故选\(D\).
法1：从数的角度分析，
由\(f(x)+2f(-x)=mx-\cfrac{1}{2}\)①，
用\(-x\)替换\(x\)得到下式
\(f(-x)+2f(x)\)\(=-mx-\cfrac{1}{2}\)②，
联立①②得到，\(f(x)=-mx-\cfrac{1}{6}\)；
则题目转化为\(-mx-\cfrac{1}{6}\geqslant lnx\)在\((0,+\infty)\)上恒成立，
分离参数得到，\(-m\geqslant \cfrac{lnx+\frac{1}{6}}{x}\)在\((0,+\infty)\)上恒成立，
令\(g(x)=\cfrac{lnx+\frac{1}{6}}{x}\)，需要求解\(g(x)\)的最大值;
\(g'(x)=\cfrac{\frac{1}{x}\cdot x-(lnx+\frac{1}{6})}{x^2}=\cfrac{\frac{5}{6}-lnx}{x^2}\)，
当\(x\in (0,e^{\frac{5}{6}})\)时，\(g'(x)>0\)，\(g(x)\)单调递增，
当\(x\in (e^{\frac{5}{6}},+\infty)\)时，\(g'(x)<0\)，\(g(x)\)单调递减，
故\(g(x)_{max}=g(e^{\frac{5}{6}})=\cfrac{lne^{\frac{5}{6}}+\frac{1}{6}}{e^{\frac{5}{6}}}=e^{-\frac{5}{6}}\)
则\(-m\geqslant e^{-\frac{5}{6}}\)，则\(m\leqslant -e^{-\frac{5}{6}}\)，故选\(B\)。
法2：从形的角度分析，
由\(f(x)+2f(-x)=mx-\cfrac{1}{2}\)①，
用\(-x\)替换\(x\)得到下式
\(f(-x)+2f(x)\)\(=-mx-\cfrac{1}{2}\)②，
联立①②得到，\(f(x)=-mx-\cfrac{1}{6}\)；
则题目转化为\(-mx-\cfrac{1}{6}\geqslant lnx\)在\((0,+\infty)\)上恒成立，
即\(-mx\geqslant lnx+\cfrac{1}{6}\)在\((0,+\infty)\)上恒成立，
设直线\(y=-mx\)与曲线\(y=lnx+\cfrac{1}{6}\)相切于点\((x_0，y_0)\)，
则有\(\left\{\begin{array}{l}{\cfrac{1}{x_0}=-m}\\{y_0=lnx_0+\cfrac{1}{6}}\\{y_0=-mx_0}\end{array}\right.\)，解得，\(x_0=e^{\frac{5}{6}}\)，\(y_0=1\)，
故相切时的斜率为\(k=\cfrac{y_0}{x_0}=\cfrac{1}{e^{\frac{5}{6}}}=e^{-\frac{5}{6}}\)，
若要满足\(-mx\geqslant lnx+\cfrac{1}{6}\)恒成立，必须满足\(-m\geqslant e^{-\frac{5}{6}}\)
则\(m\leqslant -e^{-\frac{5}{6}}\)，故选\(B\)。
分析：首先求函数\(f(x)\)的导函数如下，
\(f'(x)=(\sqrt{x})'\cdot lnx+\sqrt{x}\cdot (lnx)'\)
\(=-\cfrac{1}{2\sqrt{x}}\cdot lnx+\sqrt{x}\cdot\cfrac{1}{x}=-\cfrac{1nx}{2\sqrt{x}}+\cfrac{\sqrt{x}}{x}\)，
故\(k=f'(1)=1\)，则曲线\(y=f(x)\)在点\((1,a)\)处的切线方程为\(y-a=1\cdot(x-1)\)，
即切线方程为\(y=x+a-1\)，
将圆\(x^2+y^2-2x+4y-4=0\)化为标准形式为\((x-1)^2+(y+2)^2=3^2\)，即圆心为\((1,-2)\)，半径为\(3\)，
则圆心到切线的距离为\(d=\cfrac{|2+a|}{\sqrt{2}}\)，则弦长为\(2\sqrt{3^2-\cfrac{|2+a|^2}{2}}\)，
又由于弦长的取值范围为\([2,6]\)，即\(2\leqslant 2\sqrt{3^2-\cfrac{|2+a|^2}{2}} \leqslant 6\)
解得，\(-6\leqslant a\leqslant 2\)，即所求范围为\([-6,2]\)。[1]
分析：由已知\(a_n^2a_{n+1}+a_na_{n+1}^2=2^na_n+2^na_{n+1}\)，
变形得到\(a_na_{n+1}\cdot (a_n+a_{n+1})=2^n\cdot (a_n+a_{n+1})\)，
由于\(a_n+a_{n+1}>0\)，两边约分得到，\(a_na_{n+1}=2^n\)①，
仿照①式，构造得到\(a_{n+1}a_{n+2}=2^{n+1}\)②，
则由\(\cfrac{②}{①}\)相比得到，\(\cfrac{a_{n+2}}{a_{n}}=2\)；
又由\(a_1=1\)，\(a_n^2a_{n+1}\)\(+a_na_{n+1}^2\)\(=\)\(2^na_n+\)\(2^na_{n+1}\)，
令\(n=1\)，得到\(a_1^2a_{2}\)\(+a_1a_{2}^2\)\(=\)\(2^1a_1+\)\(2^1a_{2}\)，解得\(a_2=2\)(舍去\(a_2=-1\))，
辅助说明，数列的各项的值如下图所示：
| \(a_1=1\) | \(a_3=2\) | \(a_5=4\) | \(a_7=8\) | \(a_9=16\) | ||||
|---|---|---|---|---|---|---|---|---|
| \(a_2=2\) | \(a_4=4\) | \(a_6=8\) | \(a_8=16\) |
故数列\(\{a_n\}\)的奇数项是以\(a_1=1\)为首项，\(q=2\)为公比的等比数列；
数列\(\{a_n\}\)的偶数项是以\(a_2=2\)为首项，\(2\)为公比的等比数列；
[为了便于表达，我们采用先分后合的策略来分析，即先分析奇数项的通项公式，后分析偶数项的通项公式，]
当\(n=2k-1\)时，则\(a_{2k-1}=a_1\cdot 2^{\frac{2k-1-1}{2}}=1\cdot 2^{k-1}=2^{k-1}=2^{\frac{(2k-1)-1}{2}}\)，[2]
当\(n=2k\)时，则\(a_{2k}=a_2\cdot 2^{\frac{2k-2}{2}}=2\cdot 2^{k-1}=2^{k}=2^{\frac{2k}{2}}\)，
故所求的通项公式为\(a_n=\left\{\begin{array}{l}{2^{\frac{n-1}{2}}，n为奇数}\\{2^{\frac{n}{2}}，n为偶数}\end{array}\right.\)
则\(S_{10}=(a_1+a_3+a_5+a_7+a_9)+(a_2+a_4+a_6+a_8+a_{10})\)
\(=\cfrac{1\cdot(1-2^5)}{1-2}+\cfrac{2\cdot(1-2^5)}{1-2}=93\)；
(1).求角\(B\);
分析：由\(b=1\)，\(\cfrac{a}{c}+\cfrac{c}{a}=\cfrac{1}{ac}-1\)，
变形得到\(\cfrac{a^2+c^2}{ac}=\cfrac{1-ac}{ac}=\cfrac{b^2-ac}{ac}\)，[3]
即\(a^2+c^2-b^2=-ac\)，代入\(\cos B=\cfrac{a^2+c^2-b^2}{2ac}\)，
得到\(\cos B=\cfrac{-ac}{2ac}=-\cfrac{1}{2}\)，由于\(B\in (0,\pi)\)，
故\(B=\cfrac{2\pi}{3}\).
(2).若\(\triangle ABC\)的周长为\(1+2\sqrt{6}\)，求\(\triangle ABC\)的面积；
分析：由\(b=1\)，\(\triangle ABC\)的周长为\(1+2\sqrt{6}\)，
则\(a+c=2\sqrt{6}\)，又由于\(B=\cfrac{2\pi}{3}\)，\(b=1\)，
则由\(b^2=a^2+c^2-2ac\cos B\)，得到\(1=(a+c)^2-2ac-2ac (-\cfrac{1}{2})\)，
则解得\(ac=23\)，又由\(B=\cfrac{2\pi}{3}\)得到\(\sin B=\cfrac{\sqrt{3}}{2}\)，
故\(S_{\triangle ABC}=\cfrac{1}{2}ac\sin B=\cfrac{23\sqrt{3}}{4}\).
(1).讨论\(f(x)\)的单调性；
分析：函数的定义域为\((0,+\infty)\)，\(f'(x)=\cfrac{a}{4x}-x=\cfrac{-4x^2+a}{4x}\)，
[提示：此处可以借助函数\(y=-4x^2+a\)的图像来判断\(f'(x)\)的正负]
当\(a\leqslant 0\)时，\(f'(x)<0\)恒成立，\(f(x)\)在\((0,+\infty)\)上单调递减；
当\(a>0\)时，令\(f'(x)=0\)，得到\(x=\cfrac{\sqrt{a}}{2}\)，
则当\(0<x<\cfrac{\sqrt{a}}{2}\)时，\(f'(x)>0\)，\(f(x)\)单调递增，
当\(x>\cfrac{\sqrt{a}}{2}\)时，\(f'(x)<0\)，\(f(x)\)单调递减，
综上所述，当\(a\leqslant 0\)时，\(f(x)\)在\((0,+\infty)\)上单调递减；
当\(a>0\)时，\(f(x)\)在\((0,\cfrac{\sqrt{a}}{2})\)上单调递增，在\((\cfrac{\sqrt{a}}{2},+\infty)\)上单调递减.
(2).设\(a=4\)，且\(x\in (0,\cfrac{\pi}{6})\)，求证：\(\sqrt[4]{e}<\sqrt{e^{\cos2x}}<\frac{1}{\tan x}\);
分析：当\(a=4\)时，\(f(x)=lnx-\cfrac{1}{2}x^2\)，\(f'(x)=\cfrac{1-x^2}{x}\)，
则\(f(x)=lnx-\cfrac{1}{2}x^2\)在\((0,1)\)上单调递增，
设\(x_1\)，\(x_2\in (0,1)\)，且\(x_1<x_2\)，则有\(f(x_1)<f(x_2)\)，
即\(lnx_1-\cfrac{1}{2}x_1^2<lnx_2-\cfrac{1}{2}x_2^2\)，所以\(ln\cfrac{x_1}{x_2} < \cfrac{1}{2}(x_1^2-x_2^2)\)，
两边同时取以\(e\)为底的指数式，可得\(\cfrac{x_1}{x_2}< e^{\frac{1}{2}(x_1^2-x_2^2)}\)，
由于\(x\in (0,\cfrac{\pi}{6})\)，所以\(0<\sin x<\cos x<1\)，
所以\(\cfrac{\sin x}{\cos x}<e^{\frac{1}{2}(\sin^2x-\cos^2x)}\)，即\(\tan x<e^{-\frac{1}{2}\cos2x}\)①，
又\(x\in (0,\cfrac{\pi}{6})\)，则\(2x\in (0,\cfrac{\pi}{3})\)，
则\(\cos2x\in (\cfrac{1}{2},1)\)，\(-\cfrac{1}{2}\cos2x\in (-\cfrac{1}{2},-\cfrac{1}{4})\)，
所以\(e^{-\frac{1}{2}\cos2x}<e^{-\frac{1}{4}}\)②，
综上①②可知，\(\tan x<e^{-\frac{1}{2}\cos2x}<e^{-\frac{1}{4}}\)，又\(\tan x>0\)，
由倒数法则可得，\(\frac{1}{\tan x}>\frac{1}{e^{-\frac{1}{2}\cos2x}}>\frac{1}{e^{-\frac{1}{4}}}\)，
即\(\frac{1}{\tan x}>(e^{\cos2x})^\frac{1}{2}>e^{\frac{1}{4}}\)
即\(\sqrt[4]{e}<\sqrt{e^{\cos2x}}<\frac{1}{\tan x}\)，证毕。
分析：选\(B\)
二检典例
分析：由于\(\sqrt{3}\sin C=(\sin B+\sqrt{3}\cos B)\sin A\)，采用角化边，得到
则\(\sqrt{3}c=(\sin B+\sqrt{3}\cos B)a\)，又由于\(a=\sqrt{3}\)，[常数代换]
故\(c=(\sin B+\sqrt{3}\cos B)\)，又\(h=c\cdot \sin B\)，
则\(h=(\sin B+\sqrt{3}\cos B)\sin B=\sin(2B-\cfrac{\pi}{6})+\cfrac{1}{2}\)，
故\(h_{max}=\cfrac{3}{2}\).
提示：选\(C\)
提示：构造\(g(x)=\cfrac{f(x)}{x^2}\)，\(\forall x_1,x_2\in (0,+\infty)(x_1\neq x_2)\)
则\(\cfrac{g(x_1)-g(x_2)}{x_1-x_2}=\cfrac{\frac{f(x_1)}{x_1^2}-\frac{f(x_2)}{x_2^2}}{x_1-x_2}=\cfrac{x_2^2f(x_1)-x_1^2f(x_2)}{x_1^2x_2^2(x_1-x_2)}\)
则\(g(x)<0\)，故\(g(x)\)在\((0，+\infty)\)上单调递减，在\((-\infty,0)\)上单调递增，
又由于\(a=g(1)\)，\(b=g(2)\)，\(c=g(-3)=g(3)\)，故选\(D\).
分析：从两类符号对应的数字\(0\)和\(1\)中任取\(2\)个数字[包含两个数字相同和两个数字不相同两种情形]进行排列，
共有4种情形，列举如下，\(00_{(2)}\)、\(01_{(2)}\)、\(10_{(2)}\)、\(11_{(2)}\)；
其中\(00_{(2)}=0\times 2^1+0\times 2^0=0_{(10)}\)；\(01_{(2)}=0\times 2^1+1\times 2^0=1_{(10)}\)；
\(10_{(2)}=1\times 2^1+0\times 2^0=2_{(10)}\)；\(11_{(2)}=1\times 2^1+1\times 2^0=3_{(10)}\)；
得到的二进制数所对应的十进制数大于\(2\)的为\(11_{(2)}\)，故所求概率为\(P=\cfrac{1}{4}\)；故选\(D\);
分析：由题目可知，\(N\{f(x)\otimes g(x)\}=1\)要求\(f(x)<g(x)\)的解集中的整数解的个数为\(1\)，
当\(a\geqslant 0\)时显然不符合题意，
当\(a<0\)时，由图像可知，要满足题意，只需要\(g(2)\leqslant f(2)\)，
即\(a(2-1)^2+2\leqslant 1=log_22\)，解得\(a\leqslant -1\)，故选\(B\).
三检典例
不等式的详细求解过程如下，
左中右约分，得到\(1\leqslant \sqrt{3^2-\cfrac{|2+a|^2}{2}} \leqslant 3\)，
左中右平方，得到\(1\leqslant 9-\cfrac{|2+a|^2}{2}\leqslant 9\)，
左中右同加\(-9\)，得到\(-8=1-9\leqslant -\cfrac{|2+a|^2}{2}\leqslant 9-9=0\)，
左中右同乘以\(-1\)，得到\(0\leqslant \cfrac{|2+a|^2}{2}\leqslant 8\)，
整理为\(0\leqslant|2+a|^2\leqslant 16\)，
左中右同时开平方，得到\(0\leqslant|2+a|\leqslant 4\)，
即\(|a+2|\leqslant 4\)，即\(-4\leqslant a+2\leqslant 4\)，
解得，\(-6\leqslant a\leqslant 2\)， ↩︎对等比数列的通项公式的解释：
\(a_n=a_1\cdot q^{n-1}\)，其中\(n-1\)应该理解为第\(n\)项与第\(1\)项之间的间隔数；
当只统计所有奇数项时，第\(2k-1\)项与第\(1\)项之间的间隔数为\(\cfrac{2k-1-1}{2}=k-1\)； ↩︎此处注意两点，其一：常数的代换\(1=b\)；其二：看到左端，容易想到均值不等式，导致思维陷入僵局； ↩︎
浙公网安备 33010602011771号