数学文化题
前言
典例剖析
法1:以少御多,将无限项转化为有限项,再由多转少,这样便于思考和运算;可以假定\(n=4\),然后代入验证,选\(C\).
法2:写出新数列的通项公式\(a_k=\cfrac{1}{k}\cdot \cfrac{n}{2}\),注意通项公式不是\(a_n=\cfrac{1}{n}\cdot \cfrac{n}{2}\),
这样求和的数列的通项公式就是
\(k\ge 2\),\(a_{k-1}a_k=\cfrac{n^2}{4}\cfrac{1}{(k-1)k}=\cfrac{n^2}{4}(\cfrac{1}{k-1}-\cfrac{1}{k})\)
故\(a_1a_2+a_2a_3+a_3a_4+\cdots+a_{n-1}a_n\)
\(=\cfrac{n^2}{4}[(1-\cfrac{1}{2})+(\cfrac{1}{2}-\cfrac{1}{3})+(\cfrac{1}{3}-\cfrac{1}{4})+\cdots+(\cfrac{1}{k-1}-\cfrac{1}{k})]\)
\(=\cfrac{n^2}{4}(1-\cfrac{1}{n})=\cfrac{n(n-1)}{4}\).
分析:良马日行构成等差数列\(\{a_n\}\),其中\(a_1=103\),公差\(d_1=13\),其前\(n\)项和为\(S_n\);
驽马日行构成等差数列\(\{b_n\}\),其中\(b_1=97\),公差\(d_2=-\cfrac{1}{2}\),其前\(n\)项和为\(T_n\);
设两马\(n\)日能相逢,则由题可知,\(S_n+T_n=2\times 1125\),即\(103n+\cfrac{n(n-1)}{2}\times 13+97n+\cfrac{n(n-1)}{2} \times (-\cfrac{1}{2})=2250\),
解得\(n=9\),或者由上式直接验证得到\(n=9\),故选\(B\)。
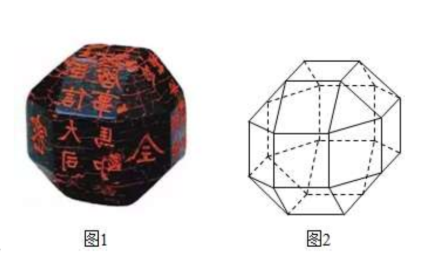
分析:半正多面体的制作过程,如下图所示;
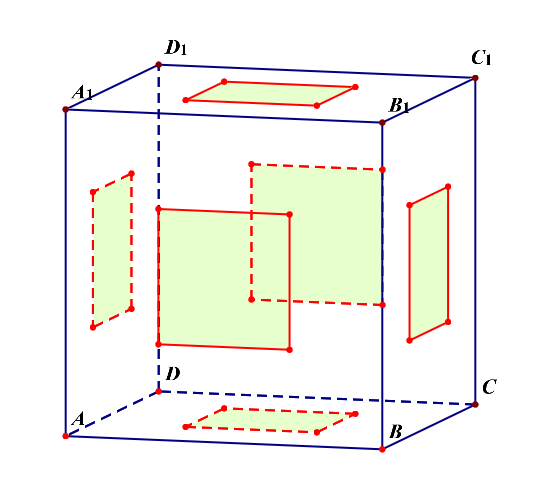
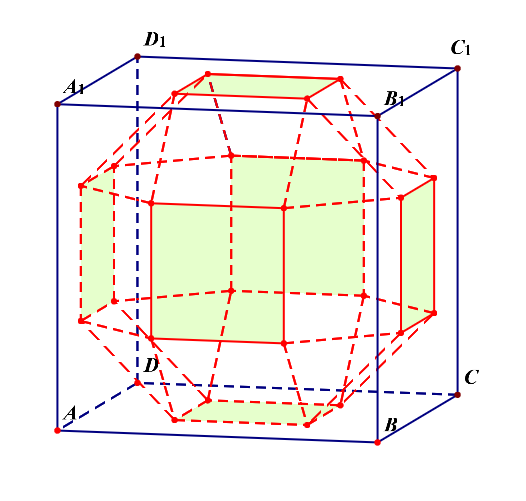
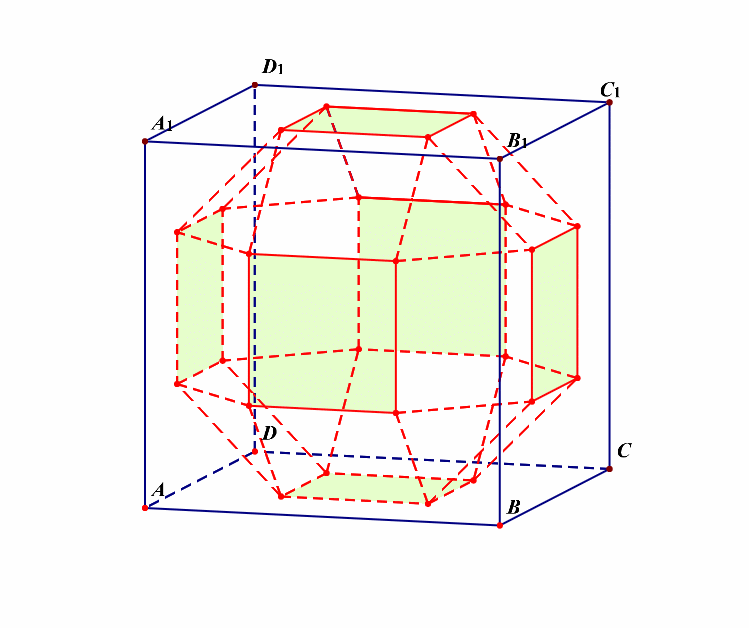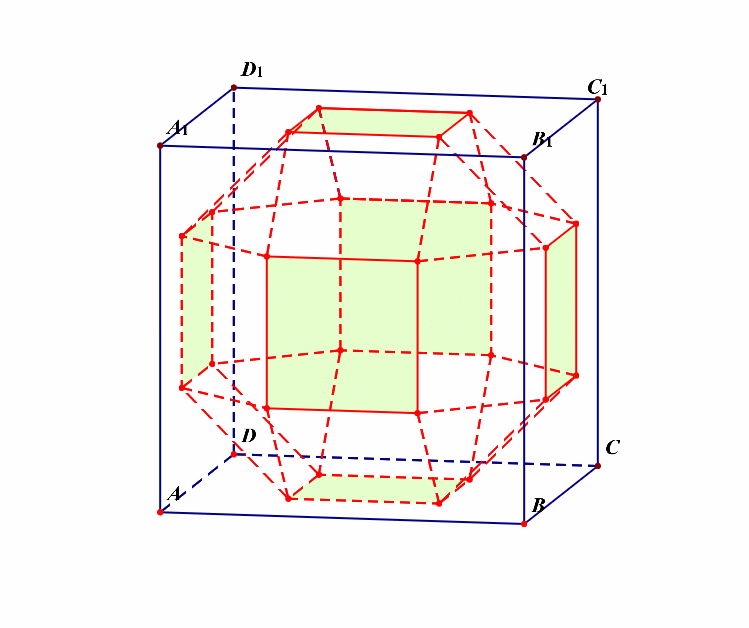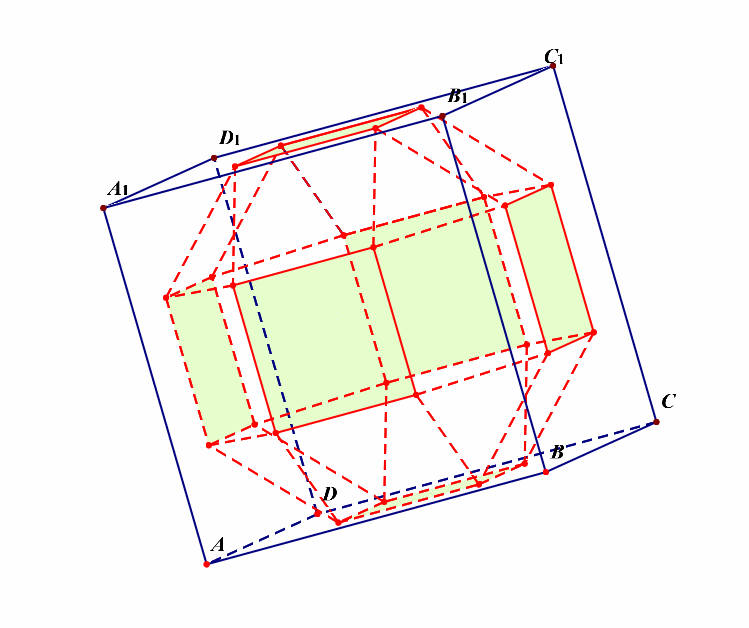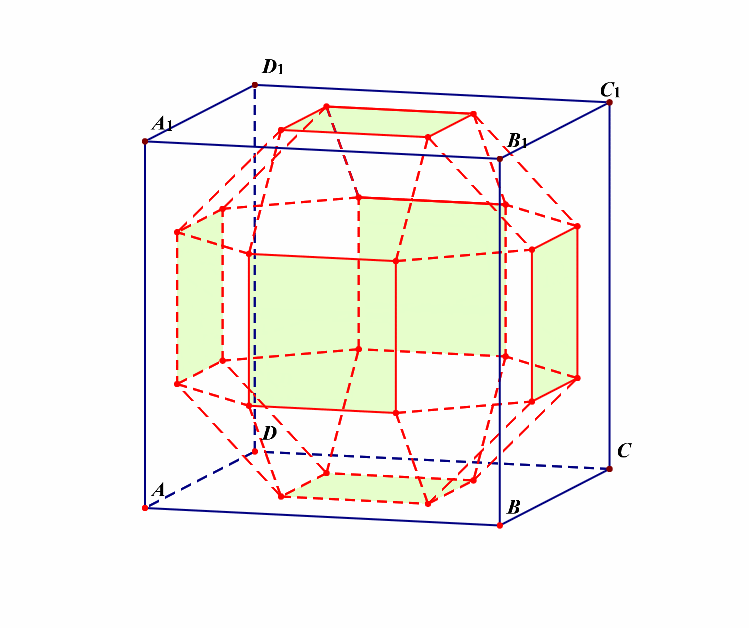
解析:如果我们将其看成是三层的,则每一层都有\(8\)个面,再外加上下两个面,故共有\(3\times 8+2=26\)个面。
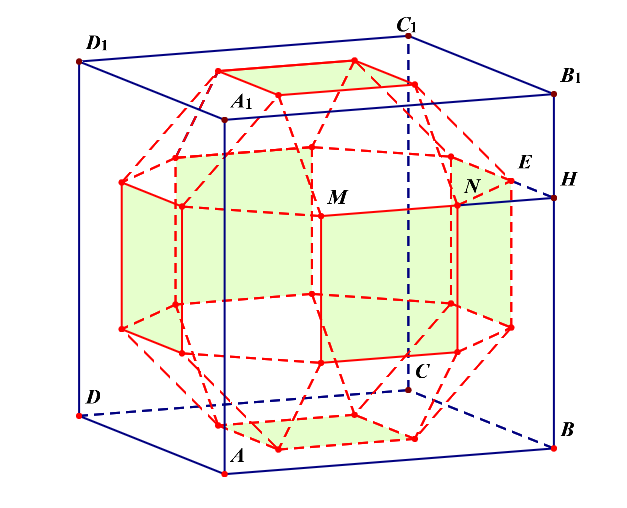
如图所示,设棱长为\(x\),即\(MN=NE=x\),由\(\triangle EHN\)为等腰直角三角形,
由\(NE=x\),则可知\(NH=\cfrac{\sqrt{2}}{2}x\),又\(MN+2NH=1\),
则\(x+2\times \cfrac{\sqrt{2}}{2}x=1\),即\((\sqrt{2}+1)x=1\),解得\(x=\sqrt{2}-1\).
综上可知,此半正多面体共有\(26\)个面,棱长为\(\sqrt{2}-1\)。
【解后反思】
1、求其表面积;
2、求其体积;
3、求其内切球的半径;
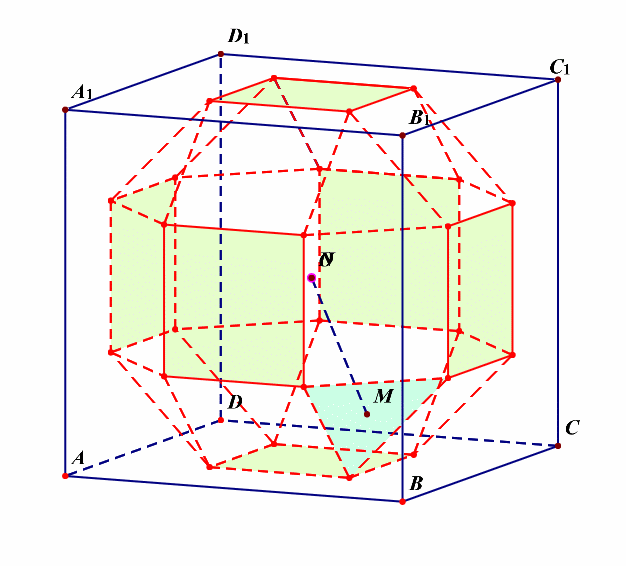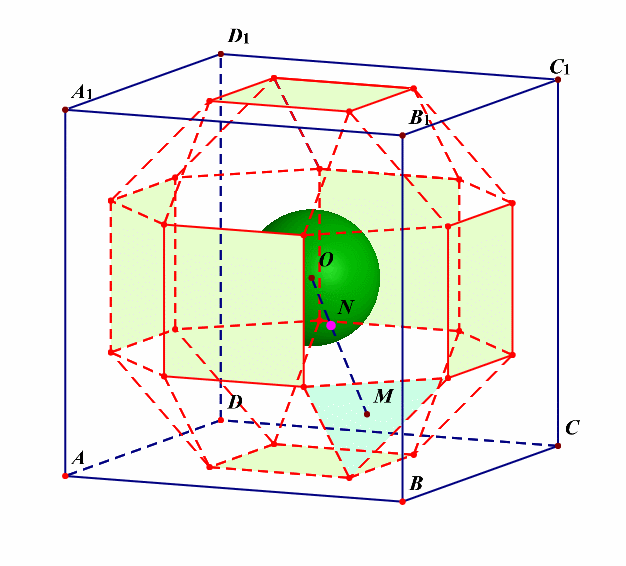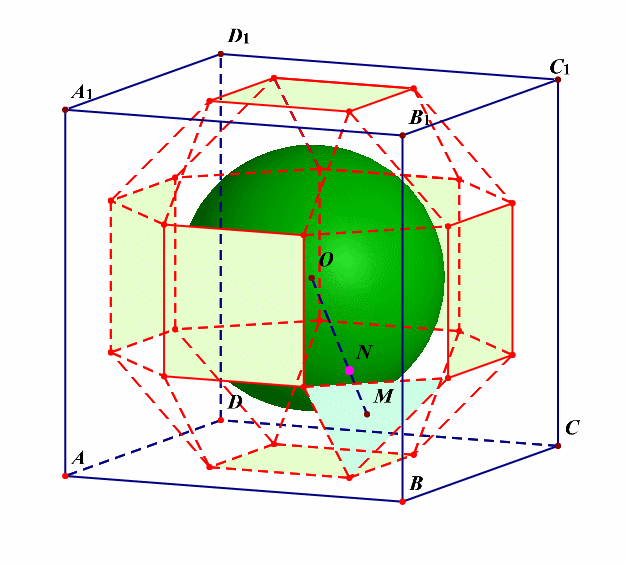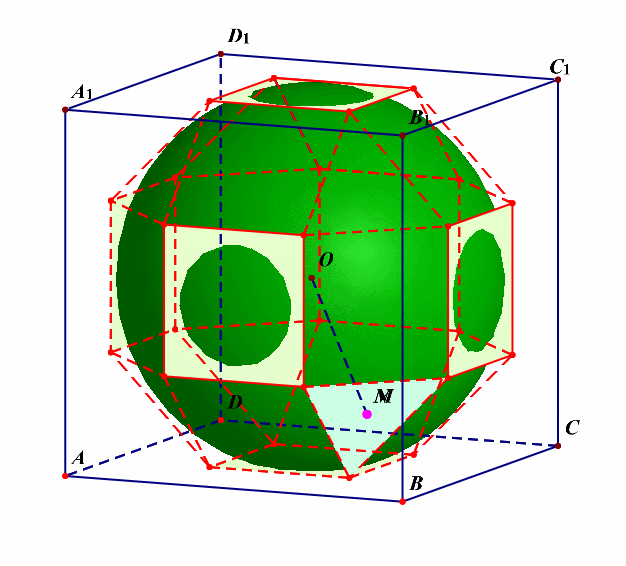
分析:由这个动画可以看出,该半正多面体没有内切球。
4、求其外接球的半径;
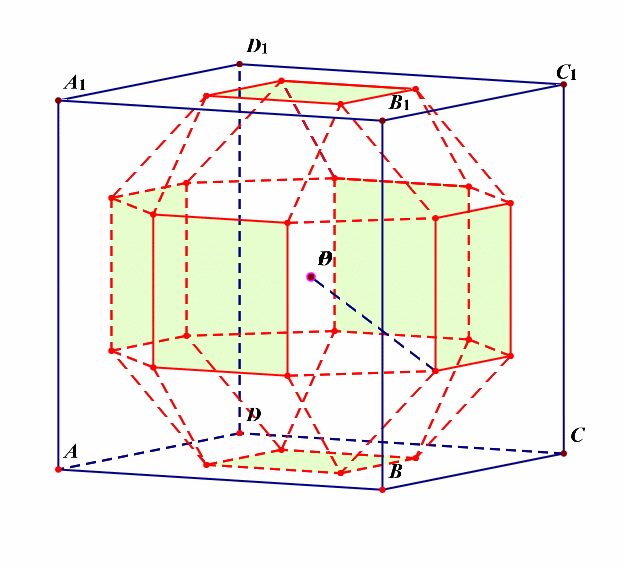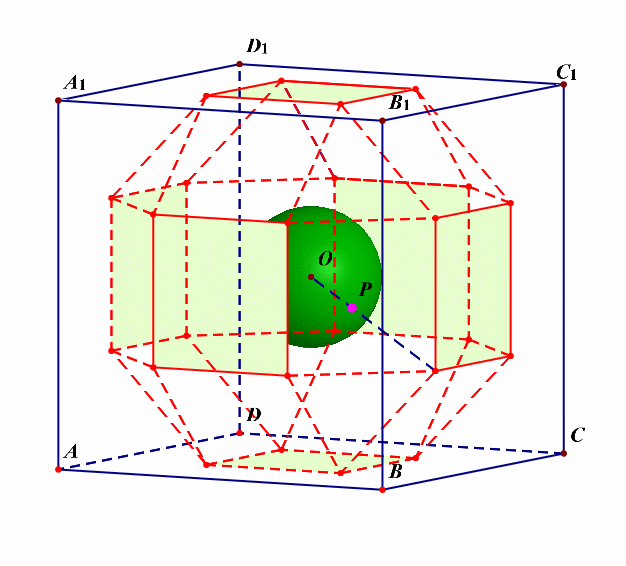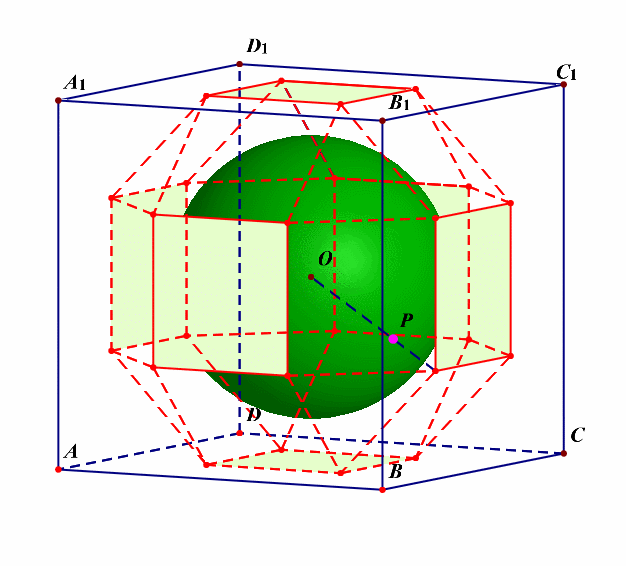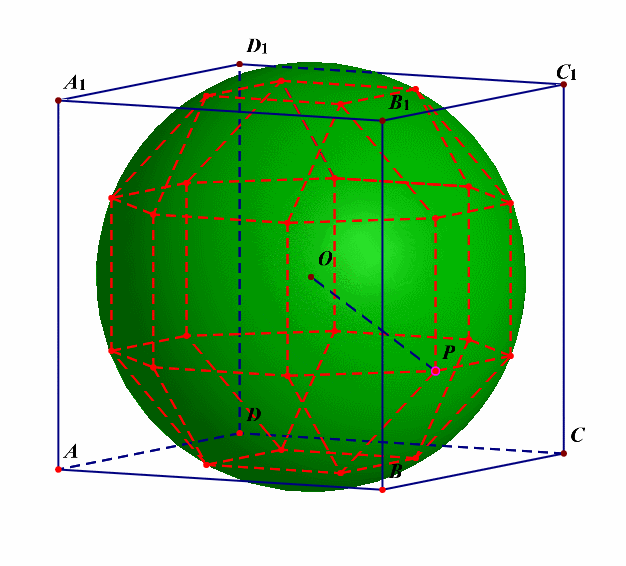
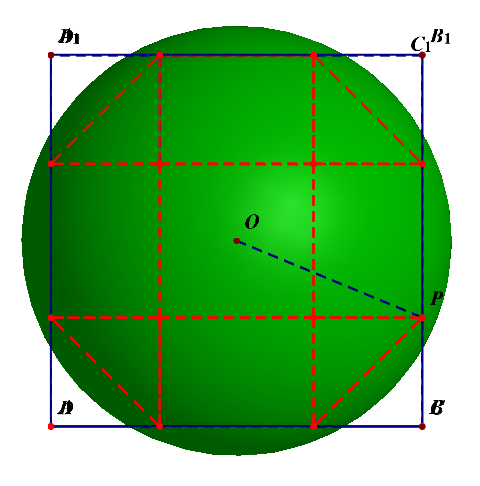
外接球的半径可以借助下图来求解。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号