三角函数单调区间

前言

请务必注意：三角函数 \(f(x)\) 的单调递增区间为 \([a,b]\) 和三角函数 \(f(x)\) 在区间 \([c,d]\) 上单调递增，是不同的两个概念；一般有 \([c,d]\)\(\subseteq\)\([a,b]\)；

整体代入法

• 直接求解三角函数的单调区间族，可以称为整体代入法，将\(\omega x+\phi(\omega>0)\)看作一个整体，代入模板函数中求解即可；

已知函数\(f(x)=2sin(2x+\cfrac{\pi}{6})+1\)， 求\(f(x)\)的单调区间；^[1]

分析：令 \(z=2x+\cfrac{\pi}{6}\)，\(z\in R\)，很显然，内函数\(z=2x+\cfrac{\pi}{6}\)为单调递增的，此时原函数变形为 \(f(x)\)\(=\)\(2\sin z\)\(+\)\(1\)，其单调区间和 \(y\)\(=\)\(\sin z\)[作减法]的单调区间相同，而 \(y=\sin z\) 的单调递增区间为 \([-\cfrac{\pi}{2}+2k\pi,\cfrac{\pi}{2}+2k\pi]\)，\(k\in Z\)，单调递减区间为 \([\cfrac{\pi}{2}+2k\pi,\cfrac{3\pi}{2}+2k\pi]\)，\(k\in Z\)，

故要求原函数的单调递增区间[内增，必须外函数要增]，只需要令\(2k\pi-\cfrac{\pi}{2}\leqslant 2x+\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{\pi}{2}\)，\(k\in Z\)，求解即可得到单调递增区间；

要求原函数的单调递减区间[内增，必须外函数要减]，只需要令\(2k\pi+\cfrac{\pi}{2}\leqslant 2x+\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{3\pi}{2}\)，\(k\in Z\)，求解即可得到单调递减区间；

解析：令\(2k\pi-\cfrac{\pi}{2}\leqslant 2x+\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{\pi}{2}\)，\(k\in Z\)，

解得单调递增区间为\([k\pi-\cfrac{\pi}{3}，k\pi+\cfrac{\pi}{6}]\)，\((k\in Z)\)；

令\(2k\pi+\cfrac{\pi}{2}\leqslant 2x+\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{3\pi}{2}\)，\(k\in Z\)，

解得单调递减区间为\([k\pi+\cfrac{\pi}{6}，k\pi+\cfrac{2\pi}{3}]\)，\((k\in Z)\)；

• 将上述求解单调区间的方法逆用，即可得到快速验证正弦型函数在某个区间的单调性；举例如下：

【改编，原题目收录在三角函数性质的综合应用里】已知函数 \(f(x)=2\sin(\omega x+\phi)\)\(\left(\omega>0，|\phi|<\cfrac{\pi}{2}\right)\)的最小正周期为 \(4\pi\)，其图像关于直线\(x=\cfrac{2\pi}{3}\) 对称，试判断以下结论的正误：

①函数\(f(x)\)在区间\([0，\cfrac{4\pi}{3}]\)上先增后减；

解析：由函数\(f(x)\)的最小正周期为\(4\pi\)，可知\(\omega=\cfrac{2\pi}{4\pi}=\cfrac{1}{2}\)，即\(f(x)=2\sin(\cfrac{1}{2}x+\phi)\)

又由于其图像关于直线\(x=\cfrac{2\pi}{3}\)对称，则函数在\(x=\cfrac{2\pi}{3}\)处的函数值必须达到最大值或者最小值，即\(f(\cfrac{2\pi}{3})=\pm 2\)，将\(x=\cfrac{2\pi}{3}\)代入得到，\(2\sin(\cfrac{1}{2}\times\cfrac{2\pi}{3}+\phi)=\pm 2\)，即\(\sin(\cfrac{\pi}{3}+\phi)=\pm1\)，即\(\cfrac{\pi}{3}+\phi=k\pi+\cfrac{\pi}{2}\)，令\(k=0\)，得到\(\phi=\cfrac{\pi}{6}\in (-\cfrac{\pi}{2},\cfrac{\pi}{2})\)，满足题意，故\(f(x)=2\sin(\cfrac{1}{2}x+\cfrac{\pi}{6})\)。当然，此时还可以利用先求解对称轴方程族，再给\(k\)赋值的方法来求解 . ^[2]

对于①而言，用验证法，由于\(0\leqslant x\leqslant\cfrac{4\pi}{3}\)，则\(\cfrac{\pi}{6}\leqslant \cfrac{1}{2}x+\cfrac{\pi}{6}\leqslant\cfrac{5\pi}{6}\)

故当\(\cfrac{\pi}{6}\leqslant \cfrac{1}{2}x+\cfrac{\pi}{6}\leqslant\cfrac{\pi}{2}\)时，即\(0\leqslant x\leqslant\cfrac{2\pi}{3}\)时，函数单调递增，

当\(\cfrac{\pi}{2}\leqslant \cfrac{1}{2}x+\cfrac{\pi}{6}\leqslant\cfrac{5}{6}\pi\)时，即\(\cfrac{2\pi}{3}\leqslant x\leqslant\cfrac{4\pi}{3}\)时，函数单调递减，故①是正确的；

当然，还有一个方法是计算法^[3]，可以先求得\(f(x)\)的所有单调区间族，然后给\(k\)赋值，看看\([0，\cfrac{4\pi}{3}]\)具体落在什么区间上再做定夺，不过这个思路会很费时间，不大可取，故上述的验证方法是最快的。

• 注意：求\(f(x)=Asin(\omega x+\phi)+k\)型函数的单调区间，为减少错误，一般需要将 \(\omega\) 转化为 \(\omega>0\) ；举例如下：

函数 \(f(x)=\sin(-2x+\cfrac{\pi}{3})\) 的单调递减区间是____________.

[正解]: 由已知可得函数为 \(y=-\sin(2 x-\cfrac{\pi}{3})\)，

欲求函数的单调减区间，只需求\(y=\sin(2x-\cfrac{\pi}{3})\) 的单调增区间此时需要将\(2x-\cfrac{\pi}{3}\)视为整体；此时依托模板函数\(y=\sin x\)的单调性求解；单增区间为\([2k\pi-\cfrac{\pi}{2},2k\pi+\cfrac{\pi}{2}]\),\((k\in Z)\)；单减区间为\([2k\pi+\cfrac{\pi}{2},2k\pi+\cfrac{3\pi}{2}]\),\((k\in Z)\)；\(\quad\)，

令 \(2k\pi-\cfrac{\pi}{2}\leqslant 2x-\cfrac{\pi}{3}\leqslant 2k\pi+\cfrac{\pi}{2}\)，\(k\in Z\)，

得 \(k\pi-\cfrac{\pi}{12} \leqslant x \leqslant k\pi+\cfrac{5\pi}{12}\)，\(k\in Z\)，

故所求函数的单调递减区间为 \([k\pi-\cfrac{\pi}{12}, k\pi+\cfrac{5\pi}{12}]\)(\(k\in Z\)).

[错解]：令 \(2k\pi+\cfrac{\pi}{2}\leqslant -2x+\cfrac{\pi}{3}\leqslant 2k\pi+\cfrac{3\pi}{2}\)，\(k\in Z\)，

得 \(-k\pi-\cfrac{7\pi}{12} \leqslant x \leqslant -k\pi-\cfrac{\pi}{12}\)，\(k\in Z\)，

也即\(k\pi-\cfrac{7\pi}{12} \leqslant x \leqslant k\pi-\cfrac{\pi}{12}\)，\(k\in Z\)，

故所求函数的单调递减区间为 \([k\pi-\cfrac{7\pi}{12}, k\pi-\cfrac{\pi}{12}]\)(\(k\in Z\)).

[错因分析]：如下图所示，正解中的单调区间为图中的红色区间集，错解中的单调区间为图中的绿色区间集，

很明显，错解将单调递增区间解成了单调递减区间；为什么会这样，原因是内函数\(y=-2x+\cfrac{\pi}{3}\)为减函数，

又将\(-2x+\cfrac{\pi}{3}\)限制在外函数的单调递减区间上，这样，减减为增，故结果是错误的；

[修正]：令 \(2k\pi-\cfrac{\pi}{2}\leqslant -2x+\cfrac{\pi}{3}\leqslant 2k\pi+\cfrac{\pi}{2}\)，\(k\in Z\)，

得到\(2k\pi-\cfrac{5\pi}{6} \leqslant -2x \leqslant 2k\pi+\cfrac{\pi}{6}\)，\(k\in Z\)，

则\(-k\pi-\cfrac{\pi}{12} \leqslant x \leqslant -k\pi+\cfrac{5\pi}{12}\)，\(k\in Z\)，

也即\(k\pi-\cfrac{\pi}{12} \leqslant x \leqslant k\pi+\cfrac{5\pi}{12}\)，\(k\in Z\)，

故所求函数的单调递减区间为 \([k\pi-\cfrac{\pi}{12}, k\pi+\cfrac{5\pi}{12}]\) (\(k\in Z\)) .

• 讨论给定区间上的三角函数的单调性，有些难度，一般可以有两个思路：①求解法+赋值法+交集法；②验证法；

【2016\(\cdot\)天津高考】已知函数\(f(x)=4tanx\cdot sin(\cfrac{\pi}{2}-x)\cdot cos(x-\cfrac{\pi}{3})-\sqrt{3}\)，

(1).求函数的定义域；

分析：由函数解析式可知，需要让\(tanx\)有意义，故定义域为\(\{x\mid x\neq k\pi+\cfrac{\pi}{2}，k\in Z\}\)

(2).试讨论\(f(x)\)在区间\([-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)上的单调性。

分析：先将所给函数化简为正弦型或者余弦型，

\(f(x)=4tanx\cdot cosx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}\)

\(=4sinx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}\)

\(=2sinxcosx+2\sqrt{3}sin^2x-\sqrt{3}\)

\(=sin2x+\sqrt{3}(1-cos2x)-\sqrt{3}\)

\(=sin2x-\sqrt{3}cos2x\)

\(=2sin(2x-\cfrac{\pi}{3})\)

法1：先求解函数在\(x\in R\)上的单调区间，

令\(2k\pi-\cfrac{\pi}{2}< 2x-\cfrac{\pi}{3}< 2k\pi+\cfrac{\pi}{2}(k\in Z)\)，

得到单调递增区间为\((k\pi-\cfrac{\pi}{12}，k\pi+\cfrac{5\pi}{12})(k\in Z)\)，

然后给\(k\)赋值，令\(k=0\)，又因为\(x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)，

[说明：求得的单调递增区间和给定区间求交集，即为所求的单调递增区间；剩余的即为单调递减区间]

得到函数在区间\((-\cfrac{\pi}{12}，\cfrac{\pi}{4}]\)上单调递增，在区间\([-\cfrac{\pi}{4}，-\cfrac{\pi}{12})\)上单调递减。

法2：验证法，由\(-\cfrac{\pi}{4}\leq x\leq \cfrac{\pi}{4}\)，求得\(-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}\)，结合横轴为\(2x-\cfrac{\pi}{3}\)的图像可知，

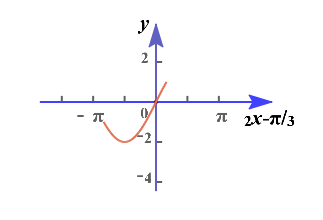
当\(-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}< -\cfrac{\pi}{2}\)时，求得函数在区间\([-\cfrac{\pi}{4}，-\cfrac{\pi}{12})\)单调递减；

当\(-\cfrac{\pi}{2}< 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}\)时，求得函数在区间\((-\cfrac{\pi}{12}，\cfrac{\pi}{4}]\)单调递增；

同增异减法

• 对于复合函数单调区间的确定，应明确：对复合过程中的每一个函数而言，同增或同减则为增，一增一减则为减，即同增异减；

【2020\(\cdot\)南昌一模】已知 \(f(x)=\cos2x+a\cos(\cfrac{\pi}{2}+x)\) 在区间 \((\cfrac{\pi}{6}, \cfrac{\pi}{2})\) 上是增函数，则实数\(a\) 的取值范围为【\(\qquad\)】

$A.[-2,+\infty)$ $B.(-2,+\infty)$ $C.(-\infty,-4)$ $D.(-\infty,-4]$

解：\(f(x)=\cos2x+a\cos(\cfrac{\pi}{2}+x)=1-2\sin^{2}x-a\sin x\)，

此函数是复合函数，内函数为\(u=\sin x\)，外函数是\(y=-2t^2-at+1\)，

由于复合函数\(f(x)\)要求在\((\cfrac{\pi}{6}, \cfrac{\pi}{2})\) 上是增函数，

而内函数\(u=\sin x\) 在 \((\cfrac{\pi}{6}, \cfrac{\pi}{2})\) 上单调递增， 且\(\sin x \in(\cfrac{1}{2}, 1)\)，

令 \(t=\sin x\)，\(t\in(\cfrac{1}{2}, 1)\)， 外函数则 \(y=-2t^{2}-at+1\)必须在\((\cfrac{1}{2}, 1)\)上单调递增，

则\(-\cfrac{a}{4}\geqslant 1\)，解得\(a\leqslant -4\)，则\(a\in(-\infty,-4]\)，故选\(D\).

图像法

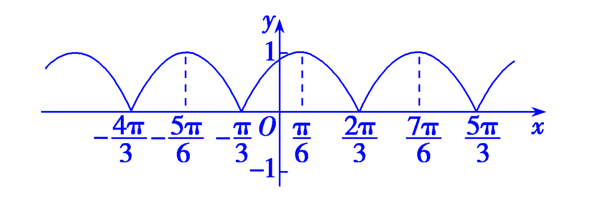
• 若函数的图像能够容易画出来，可利用图像的直观性迅速求解．同时注意函数的周期性，适合带有绝对值的三角函数单调性的判断；

设函数 \(f(x)=|\sin(x+\cfrac{\pi}{3})|(x\in R)\)，则\(f(x)\) 【\(\qquad\)】

$A.$在区间$[\cfrac{2\pi}{3},\cfrac{7\pi}{6}]$上是增函数

$B.$在区间$[-\pi,-\cfrac{\pi}{2}]$上是减函数

$C.$在区间$[-\cfrac{\pi}{3}, \cfrac{\pi}{4}]$上是增函数

$D.$在区间$[\cfrac{\pi}{3}, \cfrac{5 \pi}{6}]$上是减函数

分析：做出函数的图像如下图所示，故选\(A\).

典例剖析

【2019宝鸡质检理科第9题文科第10题】函数\(f(x)=sin(\omega x+\phi)+\sqrt{3}cos(\omega x+\phi)(\omega>0)\)的图像过点\((1，2)\)，若\(f(x)\)相邻的两个零点\(x_1\)，\(x_2\)，满足\(|x_1-x_2|=6\)，则\(f(x)\)的单调增区间为【\(\qquad\)】

$A.[-2+12k，4+12k](k\in Z)$

$B.[-5+12k，1+12k](k\in Z)$

$C.[1+12k，7+12k](k\in Z)$

$D.[-2+6k，1+6k](k\in Z)$

分析：本题目综合考查了三角函数的解析式的求解和三角函数单调区间的求解；在求解三角函数解析式时，又同时考查了整体思想；

\(f(x)=sin(\omega x+\phi)+\sqrt{3}cos(\omega x+\phi)=2sin(\omega x+\phi+\cfrac{\pi}{3})\)

由于函数图像过点\((1，2)\)，将其代入，则有\(2sin(\omega\times 1+\phi+\cfrac{\pi}{3})=2\)，

即\(\omega\times 1+\phi+\cfrac{\pi}{3}=2k\pi+\cfrac{\pi}{2}(k\in Z)\)①，

又由于\(f(x)\)相邻的两个零点\(x_1\)，\(x_2\)，满足\(|x_1-x_2|=6\) 此次还可以这样给出题目：\(x_1\)， \(x_2\)式\(f(x)\)的两个零点，且 \(|x_1-x_2|_{\min}=6\)；另外此处快速作图是个难点；\(\quad\).

则可知\(\cfrac{T}{2}=6\)，则\(T=12\)，故\(\omega=\cfrac{2\pi}{T}=\cfrac{\pi}{6}\)，

代入①式，得到\(\phi=2k\pi(k\in Z)\)，[此处对\(\phi\)的处理是个难点，由于此处只强调\(\phi\)的存在性，故从简原则，令\(k=0\)]

故得到\(\phi=0\)，即所求解析式为\(f(x)=2sin(\cfrac{\pi}{6}x+\cfrac{\pi}{3})\)，

接下来，题目转化为：给定三角函数的解析式，求其单调增区间；

令\(2k\pi-\cfrac{\pi}{2}\leqslant \cfrac{\pi}{6}x+\cfrac{\pi}{3}\leqslant 2k\pi-\cfrac{\pi}{2}(k\in Z)\)，

用常规方法求解，得到\(-5+12k\leqslant x\leqslant 1+12k(k\in Z)\)，故选\(B\)。

(三轮模拟考试理科用题)已知\(f(x)=2Acos^2(\omega x+\phi)(A>0,\omega>0,0<\phi<\cfrac{\pi}{2})\)，直线\(x=\cfrac{\pi}{3}\)和点\((\cfrac{\pi}{12},0)\)分别是函数\(f(x)\)图象上相邻的一条对称轴和一个对称中心，则函数\(f(x)\)的单调增区间为【\(\qquad\)】.

$A.[k\pi-\cfrac{2\pi}{3} ，k\pi-\cfrac{\pi}{6}](k\in Z)$

$B.[k\pi-\cfrac{\pi}{6} ，k\pi+\cfrac{\pi}{3}](k\in Z)$

$C.[k\pi-\cfrac{5\pi}{12} ，k\pi+\cfrac{\pi}{12}](k\in Z)$

$D.[k\pi+\cfrac{\pi}{12} ，k\pi+\cfrac{7\pi}{12}](k\in Z)$

分析：这类题目一般需要先将\(f(x)\)转化为正弦型或者余弦型，再利用给定的条件分别求\(\omega\)和\(\phi\)，由

\(f(x)=2Acos^2(\omega x+\phi)=A[cos2(\omega x+\phi)+1]=Acos(2\omega x+2\phi)+A\)，

故其周期为\(T=\cfrac{2\pi}{2\omega}=\cfrac{\pi}{\omega}\)，又由题目可知\(\cfrac{T}{4}=\cfrac{\pi}{3}-\cfrac{\pi}{12}=\cfrac{\pi}{4}\)，则\(T=\pi=\cfrac{\pi}{\omega}\)，

故\(\omega=1\)，则函数简化为\(f(x)=Acos(2x+2\phi)+A\)，再利用直线\(x=\cfrac{\pi}{3}\)是函数\(f(x)\)图象上的一条对称轴，

故\(2\times \cfrac{\pi}{3}+2\phi=k\pi,(k\in Z)\),解得\(\phi=\cfrac{k\pi}{2}-\cfrac{\pi}{3}\)，

令\(k=1\)，则\(\phi=\cfrac{\pi}{6}\in (0,\cfrac{\pi}{2})\)，满足题意，故\(f(x)=Acos(2x+2\phi)+A=Acos(2x+\cfrac{\pi}{3})+A\).

令\(2k\pi-\pi\leq 2x+\cfrac{\pi}{3}\leq 2k\pi(k\in Z)\)，解得\(k\pi-\cfrac{2\pi}{3}\leq x \leq k\pi-\cfrac{\pi}{6}(k\in Z)\)，故选\(A\);

• 已知三角函数单调区间，求参数的取值范围；

【2018全国高考Ⅱ卷第10题】若\(f(x)=cosx-sinx\)在\([0，a]\)上是减函数，则\(a\)的最大值是【\(\qquad\)】

$A.\cfrac{\pi}{4}$ $B.\cfrac{\pi}{2}$ $C.\cfrac{3\pi}{4}$ $D.\pi$

法1： 由于\(f(x)=\cos x-\sin x=-\sqrt{2}\sin(x-\cfrac{\pi}{4})\)，

故当\(x-\cfrac{\pi}{4}\in[-\cfrac{\pi}{2}, \cfrac{\pi}{2}]\)，即\(x\in[-\cfrac{\pi}{4}, \cfrac{3\pi}{4}]\)时，

\(\sin(x-\cfrac{\pi}{4})\)单调递增，则\(-\sqrt{2}\sin(x-\cfrac{\pi}{4})\) 单调递减，

则\([-\cfrac{\pi}{4}, \cfrac{3\pi}{4}]\) 是 \(f(x)\) 在原点附近的单调减区间，

结合条件得\([0, a]\subsetneqq[-\cfrac{\pi}{4}, \cfrac{3\pi}{4}]\)，

故有 \(0<a\leqslant\cfrac{3\pi}{4}\)，即 \(a_{max}=\cfrac{3\pi}{4}\)，故选\(C\).

法2：由题目可知，\(f'(x)=-sinx-cosx\leq 0\)在\([0，a]\)上恒成立，即\(sinx+cosx\ge 0\)在\([0，a]\)上恒成立，

即\(sinx+cosx=\sqrt{2}sin(x+\cfrac{\pi}{4})\geqslant 0\)在\([0，a]\)上恒成立，将\(4\)个选项代入验证，

满足题意\(\sin x+\cos x\geqslant 0\)恒成立的选项有\(A\)，\(B\)，\(C\)， 其中只有选项\(C\)使得\(a\)最大，故选\(C\)。

法3：由于\(f^{\prime}(x)=-\sin x-\cos x=-\sqrt{2}\sin(x+\cfrac{\pi}{4})\)

于是，由题设得 \(f^{\prime}(x) \leqslant 0\),

即 \(\sin(x+\cfrac{\pi}{4}) \geqslant 0\) 在区间 \([0, a]\) 上恒成立.

当 \(x \in[0, a]\) 时, \(x+\cfrac{\pi}{4} \in[\cfrac{\pi}{4}, a+\cfrac{\pi}{4}]\)，

所以 \(a+\cfrac{\pi}{4} \leqslant \pi\)， 即 \(a \leqslant \cfrac{3 \pi}{4}\)，

故所求 \(a\) 的最大值是 \(\cfrac{3 \pi}{4}\).故选 \(C\).

法4：由于\(f(x)=cosx-sinx=\sqrt{2}cos(x+\cfrac{\pi}{4})\)，

做出函数\(f(x)\)的图像，观察发现，\(a\)的最大值是\(\cfrac{3\pi}{4}\)，故选\(C\)。

法5：集合法，\(f(x)=cosx-sinx=\sqrt{2}cos(x+\cfrac{\pi}{4})\)，

由\(0+2k\pi\leq x+\cfrac{\pi}{4}\leq \pi+2k\pi(k\in Z)\)，得到\(-\cfrac{\pi}{4}+2k\pi\leq x\leq \cfrac{3\pi}{4}+2k\pi(k\in Z)\)，

因此，\([0，a]\subseteq [-\cfrac{\pi}{4}，\cfrac{3\pi}{4}]\)，又由于\(0< a\)，

则\(0< a\leq \cfrac{3\pi}{4}\)，故\(a_{max}=\cfrac{3\pi}{4}\)，故选\(C\)。

【2022届高三一轮复习资料用题改编】 已知函数 \(f(x)=2\sin\left(2x-\cfrac{\pi}{6}\right)+1\) .

(1).求函数 \(f(x)\) 在区间 \([-\cfrac{\pi}{3},\cfrac{5\pi}{6}]\) 上的单调性；

法1：利用 \(R\) 上的单调区间和给定区间求交集法；

令\(2k\pi-\cfrac{\pi}{2}\leqslant 2x-\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{\pi}{2}\)，\((k\in Z)\)，

解得 \(R\) 上的单调递增区间为 \([k\pi-\cfrac{\pi}{6},k\pi+\cfrac{\pi}{3}]\)，\((k\in Z)\)，

将其和给定区间 \([-\cfrac{\pi}{3},\cfrac{5\pi}{6}]\) 求交集，得到单调递增区间为 \([-\cfrac{\pi}{6},\cfrac{\pi}{3}]\)；

令\(2k\pi+\cfrac{\pi}{2}\leqslant 2x-\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{3\pi}{2}\)，\((k\in Z)\)，

解得 \(R\) 上的单调递减区间为 \([k\pi+\cfrac{\pi}{3},k\pi+\cfrac{5\pi}{6}]\)，\((k\in Z)\)，

将其和给定区间 \([-\cfrac{\pi}{3},\cfrac{5\pi}{6}]\) 求交集，得到单调递减区间为 \([-\cfrac{\pi}{3},-\cfrac{\pi}{6}]\) 和 \([\cfrac{\pi}{3},\cfrac{5\pi}{6}]\) ；

法2：利用整体思想求解，

由于 \(-\cfrac{\pi}{3}\leqslant x\leqslant \cfrac{5\pi}{6}\)，则 \(-\cfrac{2\pi}{3}\leqslant 2x\leqslant \cfrac{5\pi}{3}\)，则有 \(-\cfrac{5\pi}{6}\leqslant 2x-\cfrac{\pi}{6}\leqslant \cfrac{3\pi}{2}\)，

以 \(2x-\cfrac{\pi}{6}\) 的整体为横轴，做函数图像，结合图像可知，

当 \(-\cfrac{5\pi}{6}\leqslant 2x-\cfrac{\pi}{6}\leqslant -\cfrac{\pi}{2}\) 时，即 \(-\cfrac{\pi}{3}\leqslant x\leqslant -\cfrac{\pi}{6}\) 时，函数单调递减，

当 \(-\cfrac{\pi}{2}\leqslant 2x-\cfrac{\pi}{6}\leqslant \cfrac{\pi}{2}\) 时，即 \(-\cfrac{\pi}{6}\leqslant x\leqslant \cfrac{\pi}{3}\) 时，函数单调递增，

当 \(\cfrac{\pi}{2}\leqslant 2x-\cfrac{\pi}{6}\leqslant \cfrac{3\pi}{2}\) 时，即 \(\cfrac{\pi}{3}\leqslant x\leqslant \cfrac{5\pi}{6}\) 时，函数单调递减，

故得到单调递减区间为 \([-\cfrac{\pi}{3},-\cfrac{\pi}{6}]\) 和 \([\cfrac{\pi}{3},\cfrac{5\pi}{6}]\)，单调递增区间为 \([-\cfrac{\pi}{6},\cfrac{\pi}{3}]\)；

---

1. 在实际问题中，很可能不是直接给出正弦型，而需要我们首先将其化简为正(余)弦型；举例如下：
   \(f(x)=\cfrac{\sqrt{3}}{3}[cos(2x+\cfrac{\pi}{6})+4sinxcosx]+1\)，\(x\in R\)，
   \(f(x)=\cfrac{\sqrt{3}}{3}[cos(2x+\cfrac{\pi}{6})+4sinxcosx]+1\)，
   \(=\cfrac{\sqrt{3}}{3}[(cos2x\cdot cos\cfrac{\pi}{6}-sin2x\cdot sin\cfrac{\pi}{6})+2sin2x]+1\)
   \(=\cfrac{\sqrt{3}}{3}(\cfrac{\sqrt{3}}{2}cos2x-\cfrac{1}{2}sin2x+2sin2x)+1\)
   \(=\cfrac{\sqrt{3}}{3}(\cfrac{\sqrt{3}}{2}cos2x+\cfrac{3}{2}sin2x)+1\)
   \(=\cfrac{\sqrt{3}}{2}sin2x+\cfrac{1}{2}cos2x+1\)
   \(=sin(2x+\cfrac{\pi}{6})+1\)， [化简到此结束] ↩︎

2. 由 \(f(x)=2\sin(\cfrac{1}{2}x+\phi)\) 可知， 令 \(\cfrac{1}{2}x+\phi=k\pi+\cfrac{\pi}{2}\)，
   解得函数的对称轴方程为 \(x=2k\pi+\pi-2\phi\)，\(k\in Z\)，又由题目可知直线 \(x=\cfrac{2\pi}{3}\) 为其一条对称轴，
   令 \(2k\pi+\pi-2\phi=\cfrac{2\pi}{3}\) ，\(k\in Z\)，即得到 \(\phi=k\pi+\cfrac{\pi}{6}\)，\(k\in Z\)，令 \(k=0\)，即得到 \(\phi=\cfrac{\pi}{6}\in (-\cfrac{\pi}{2},\cfrac{\pi}{2})\) ↩︎

3. 令 \(2k\pi-\cfrac{\pi}{2}\leqslant \cfrac{1}{2}x+\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{\pi}{2}\) ，\(k\in Z\)，
   解得，\(4k\pi-\cfrac{4\pi}{3}\leqslant x\leqslant 4k\pi+\cfrac{2\pi}{3}\) ，\(k\in Z\)，
   令 \(k=0\)，即 距离原点最近的单调递增区间为 \([-\cfrac{4\pi}{3},\cfrac{2\pi}{3}]\) ，
   现在题目限定的区间为 \([0，\cfrac{4\pi}{3}]\) ，故在区间 \([0，\cfrac{2\pi}{3}]\) 上单调递增，
   同理， 令 \(2k\pi+\cfrac{\pi}{2}\leqslant \cfrac{1}{2}x+\cfrac{\pi}{6}\leqslant 2k\pi+\cfrac{3\pi}{2}\) ，\(k\in Z\)，
   解得，\(4k\pi+\cfrac{2\pi}{3}\leqslant x\leqslant 4k\pi+\cfrac{8\pi}{3}\) ，\(k\in Z\)，
   令 \(k=0\)，即 距离原点最近的单调递减区间为 \([\cfrac{2\pi}{3},\cfrac{8\pi}{3}]\) ，
   现在题目限定的区间为 \([0，\cfrac{4\pi}{3}]\) ，故在区间 \([\cfrac{2\pi}{3}，\cfrac{4\pi}{3}]\) 上单调递减。 ↩︎