区间断想

前言

集合与区间

表示集合的形式有列举法，描述法，区间法，字母法，韦恩图法，区间仅仅是集合的表示形式之一。比如区间\([a,b]\)，我们一般认为其\(a\leqslant b\)，当\(a=b\)时可以理解为区间退化为一个点。为便于理解和描述，我们可以称端点值为定值的区间\([2,3]\)为定区间，称端点值为变化的值的区间\([m+1,2m-1](m\in R)\)为动区间。这样就涉及到如何刻画一个区间为空集和非空集合的问题。

已知集合\(A=\{x\mid -2\leq x\leq 7\}\)，集合\(B=\{x\mid m+1< x<2m-1 \}\)，若\(B\subseteq A\)，则实数\(m\)的取值范围是什么？

分析：集合\(A\)为定集，集合\(B\)为动集，又因为出现了条件\(B\subseteq A\)，故需要针对集合\(B\)分类讨论如下：

1、当集合\(B=\varnothing\)时，则有\(m+1\ge 2m-1\)，解得\(m\leq 2\)；

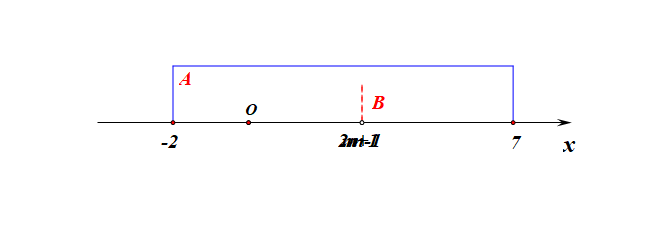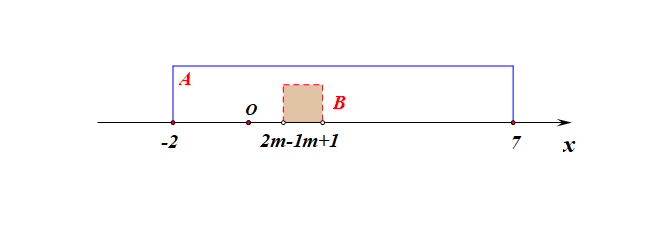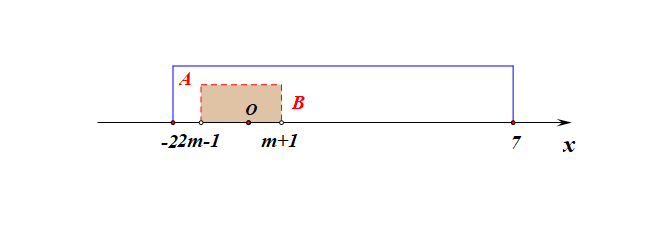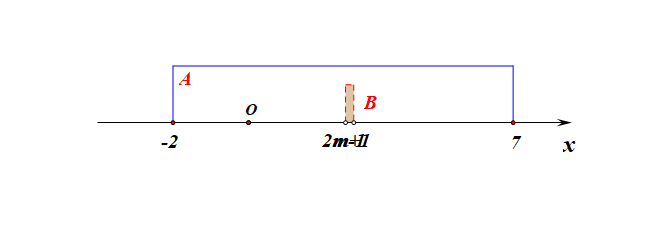
2、当集合\(B\neq\varnothing\)时，必须满足三个条件，即 \(\left\{\begin{array}{l}{m+1< 2m-1}\\{ -2 \leq m+1}\\{2m-1 \leq7}\end{array}\right.\)，解得\(2<m\leq 4\)；

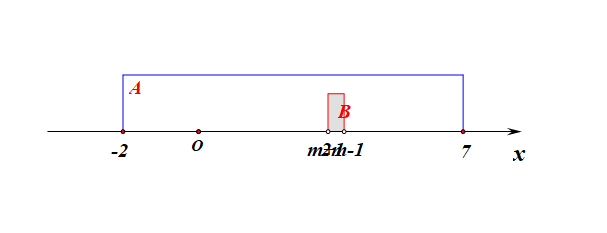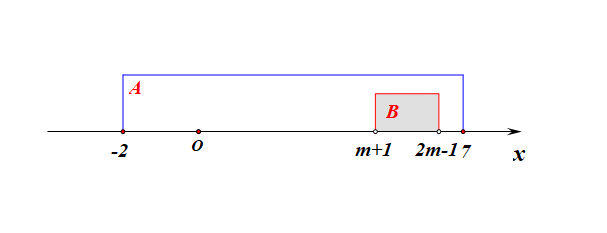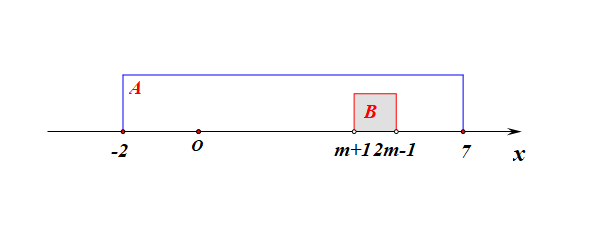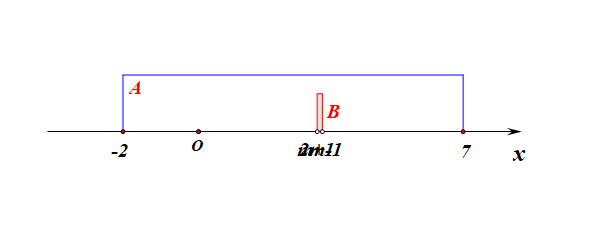
综上所述：实数\(m\)的取值范围是\(\{m\mid m\leq 4\}\)。

取值范围与区间

涉及到取值范围的问题，初中我们还可以用 \(2<x<3\) 这样的不等式形式来刻画取值范围，但是当我们学习了集合这一工具以后，我们一般就转为采用集合的相关表示形式来刻画，比如采用区间\((2,3)\)或者\(\{x\mid 2<x<3\}\)，更多采用区间来描述，很明显这种表示简单快捷。当我们强迫自己这样适应或者有意识这样适应还有一个好处，碰到求单调区间的问题，自然就不会将结果写成单调区间为\(2<x<3\)，而会自然而然的写为区间\((2，3)\)。

另外，碰到求定义域，值域，方程的解集，不等式的解集问题，我们自然也应该想到用集合的相关表示形式来刻画。

单调性与区间

在刻画函数的单调性的时候，首先涉及到的概念就是区间[连续型函数]或者定义域的子集[离散型函数]，由于函数的单调性是函数的局部性质，不一定是函数的定义域上的共有性质，故先取定义域内的某一个区间\(D\)[或子集]来刻画，如果\(x_1<x_2\in D\)，满足\(f(x_1)<f(x_2)\)，则称函数\(f(x)\)在区间\(D\)上是增加的，比如函数\(f(x)=x^2\)，在区间\((-\infty，0]\)上是减少的(或者称为递减的)，在区间\([0，+\infty)\)上增加的(或者称为递增的)，我们称区间\((-\infty，0]\)为单调递减区间，称区间\([0，+\infty)\)为单调递增区间，单调递减区间和单调递增区间合称单调区间。

大多函数在定义域的区间上有增有减，还有些函数在其定义域上只有增加的或者只是减少的，说明这样的函数相比其他的函数显得更纯粹，更特殊，可以将这样的函数重新定义，以便于和其他的函数区分开来。比如\(f(x)=2^x\)在其定义域\((-\infty，+\infty)\)上只是增加的，这就显得很特殊，此时我们就称这个函数是增函数，同理函数\(g(x)=(\cfrac{1}{e})^x\)为减函数；将增函数和减函数统称为单调函数。如果函数有单调性，我们自然想知道函数在哪些区间上是增加的，哪些区间上是减少的，故涉及到求函数的单调区间问题以及单调区间的写法。

求单调区间

写出函数\(f(x)=\cfrac{1}{x}\)的单调区间。

分析：函数的定义域为\((-\infty，0)\cup (0，+\infty)\)，不能写成\((-\infty，0)\)和\((0，+\infty)\)，也不能写成\((-\infty，0)\)或\((0，+\infty)\)；

单调递减区间为\((-\infty，0)\)和\((0，+\infty)\)，或者写成单调递减区间为\((-\infty，0)\)，\((0，+\infty)\)；不能写成\((-\infty，0)\cup (0，+\infty)\)。

上述的叙述弄糊涂了好多学生，到底怎么理解呢？

函数的定义域是自变量的取值集合，既然为集合，就应该写成\((-\infty，0)\cup (0，+\infty)\)，区间与区间之间的符号应该用符号\(\cup\)，而不是用文字和，或等，故定义域不能写成\((-\infty，0)\)和\((0，+\infty)\)，也不能写成\((-\infty，0)\)或\((0，+\infty)\)；

那么上述的单调递减区间为什么必须写成\((-\infty，0)\)和\((0，+\infty)\)呢？这样写意味着我们刻画单调性时，取自变量\(x_1\)，\(x_2\)只能取自区间\((-\infty，0)\)，或者只能取自区间\((0，+\infty)\)，此时如果令\(x_1<x_2<0\)，或者\(0<x_1<x_2\)，由图像都会得到\(f(x_1)>f(x_2)\)，故函数在区间\((-\infty，0)\)和\((0，+\infty)\)上都是单调递减的；

如果将单调递减区间写成\((-\infty，0)\cup (0，+\infty)\)，则意味着我们刻画单调性时，取自变量\(x_1\)，\(x_2\)时可以跨区间取值，即\(x_1\in (-\infty，0)\)，\(x_2\in (0，+\infty)\)，则必然有\(x_1<x_2\)，而由图像很明显可以得到\(f(x_1)<f(x_2)\)，这样的话函数应该是单调增加的，我们都知道这样的结论是错误的，究其原因，函数在点\(x=0\)处的图像是不连续的，且函数在点\(x=0\)的两侧的函数值发生了很大的变化。

区间的并与不并

【函数性质综合应用中的难点】注意对比两个例子中的单调性和图像，比如

①已知定义在\(R\)上的奇函数\(f(x)\)，在\((0，+\infty)\)上单调递增，则函数图像可能是①，而不可能是②；此时的单调区间就不能写成\((-\infty，0)\cup (0，+\infty)\)。

②已知定义在\(R\)上的奇函数\(f(x)\)，在\([0，+\infty)\)上单调递增，则函数图像可能是②，而不可能是①；此时的单调区间就必须写成\((-\infty，0]\cup [0，+\infty)\)，即\((-\infty，+\infty)\)，即函数是增函数，以便于我们利用增函数这条性质解决更多的问题。

备注：如果区间之间有间隔，比如区间\([1,2]\)和\([3,4]\)，即使单调性相同，也不能写成并集。

已知奇函数\(f(x)\)的定义域为\([-2，2]\)，且在区间\([0，2]\)单调递增，求解不等式\(f(3x+1)>f(1-2x)\)，

分析：由区间\([0，2]\)单调递增，和奇函数可知，则函数在区间\([-2，0]\)上单调递增，

故函数\(f(x)\)在区间\([-2，2]\)单调递增，

再由定义域和单调性可知\(\left\{\begin{array}{l}{-2\leq 3x+1\leq 2}\\{-2\leq 1-2x\leq 2}\\{3x+1>1-2x}\end{array}\right.\)

解集，略。

说明：定义域上的单调性没有直接给出，需要我们借助奇偶性自行推导。