求三角形面积的最值[范围]
前言
三角形的面积公式,我们从小学开始学习,一直学习到高中、大学,求三角形面积的最值类题目也越来越难,到底该如何牵住这条牛鼻子呢?
公式总结
\(S_{\triangle ABC}=\cfrac{1}{2}\cdot a\cdot h_a\);小学数学中的内容,
\(S_{\triangle ABC}=\cfrac{1}{2}absinC=\cfrac{1}{2}bcsinA=\cfrac{1}{2}casinB\);高中内容,应用在极坐标系中在极坐标系中,面积公式可能是这样的:\(S_{\triangle ABC}\) \(=\) \(\cfrac{1}{2}\) \(\cdot\) \(\rho_1\) \(\cdot\) \(\rho_2\) \(\cdot\) \(\sin\theta\),其中 \(\theta\) 为 \(\rho_1\) 和 \(\rho_2\) 的夹角,;
\(S_{\triangle ABC}=\cfrac{1}{2}(a+b+c)\cdot r\),其中\(r\)为内切圆的半径;高中的内容
\(S_{\triangle ABC}=\cfrac{abc}{4R}\),其中\(R\)为外接圆的半径;高中的内容
\(S_{\triangle ABC}=\sqrt{p(p-a)(p-b)(p-c)}\),其中\(p=\cfrac{1}{2}(a+b+c)\),海伦公式;高中或大学的内容
间接求解,如 \(S_{\triangle ABC}=S_{\triangle BCD}-S_{\triangle ACD}\),比如用割补法,初高中内容
命题研究
强烈建议你,下述内容可以先跳过,等到所有的例题理解透彻后再来理解以下内容,会比较适合。
对\(S_{\triangle ABC}=\cfrac{1}{2}\cdot a\cdot h_a\)而言,若已知三角形的底边\(a\)是常数,则其范围或最值就只取决于这一边上的高\(h_a\),故求最值或者范围就转化为求高的最值或者范围,或者换过来,令\(h_a\)是常数,则又取决于底边\(a\)的最值或者范围;又或者\(a\)和\(h_a\)的和为定值,这时候可以利用均值不等式来考查;
对\(S_{\triangle ABC}=\cfrac{1}{2}absinC\)[仅仅取一个形式说明]而言,若\(\angle C\)是常数,则其范围或最值就只取决于\(ab\),若题目已知\(a+b=2\)或者\(2a+b=2\),则可以借助均值不等式来考查面积的最大值,又或者在\(\angle C\)是常数的基础上添加\(c=2\)[定值],则\(2R=\cfrac{c}{\sin C}\)可知,此时\(a=2R\cdot\sin A\),\(b=2R\cdot\sin B\),则面积的表达式可以转化为正弦型函数,从而借助三角函数的性质来考查面积的取值范围,这种考查角度对现在的高中生来说是个大难点,尤其是其中涉及到的运算。在极坐标系中,面积公式可能是这样的:\(S_{\triangle ABC}\)\(=\)\(\cfrac{1}{2}\)\(\cdot\)\(\rho_1\)\(\cdot\)\(\rho_2\)\(\cdot\)\(\sin\theta\),其中\(\theta\)为\(\rho_1\)和\(\rho_2\)的夹角;
对\(S_{\triangle ABC}=\sqrt{p(p-a)(p-b)(p-c)}\),其中\(p=\cfrac{1}{2}(a+b+c)\)而言,高中阶段考查到的频次比较小,不过若给定了三角形一边的长度,和另外两边的关系,比如\(a=2\),\(b=c+3\),则设\(c=x\),\(b=3+x\),这样三角形的三边就变化为\(2\),\(x\),\(x+3\),这样三角形的面积就可以使用海伦公式来刻画,从而\(S=S(x)\),从而可以借助函数的性质求解三角形面积的最值,或者由最值求解三角形中的其他量。
典例剖析
(1)求角\(B\).
分析:由于\(a\cdot\sin\cfrac{A+C}{2}=b\cdot\sin A\),即为\(a\cdot\sin\cfrac{\pi-B}{2}=a\cdot\cos\cfrac{B}{2}=b\cdot\sin A\)
可得 \(\sin A\cdot\cos\cfrac{B}{2}=\sin B\cdot\sin A=2\sin\cfrac{B}{2}\cdot\cos\cfrac{B}{2}\cdot\sin A\),
\(\because \sin A>0\),\(\therefore \cos\cfrac{B}{2}=2\sin\cfrac{B}{2}\cdot\cos\cfrac{B}{2}\),
即\(\cos\cfrac{B}{2}\cdot (2\sin\cfrac{B}{2}-1)=0\),
若\(\cos\cfrac{B}{2}=0\),可得\(B=\pi\),不符题意,舍去;
\(\therefore\sin\cfrac{B}{2}=\cfrac{1}{2}\),由\(0<B<\pi\), 可得\(B=\cfrac{\pi}{3}\).
(2)若\(\triangle ABC\)为锐角三角形,且\(c=1\),求\(\triangle ABC\)面积的取值范围.
[法1]:结合已知条件,从边的角度思考和刻画,转化为关于边的函数求解;
若\(\triangle ABC\)为锐角三角形,且\(c=1\),
由余弦定理\(b^2=a^2+c^2-2a\cdot c\cdot\cos B\)可得,
\(b=\sqrt{a^{2}+1^2-2 a\cdot1\cdot\cos\cfrac{\pi}{3}}=\sqrt{a^{2}-a+1}\)
由三角形\(ABC\)为锐角三角形,则必须满足条件\(\left\{\begin{array}{l}{b^2+c^2>a^2}\\{a^2+c^2>b^2}\\{a^2+b^2>c^2}\end{array}\right.\)
可得到\(\left\{\begin{array}{l}{a^{2}+a^{2}-a+1>1}\\{1+a^{2}-a+1>a^{2}}\\{1+a^{2}>a^{2}-a+1}\end{array}\right.\),解得\(\cfrac{1}{2}<a<2\),
可得\(\triangle ABC\)面积
\(S=\cfrac{1}{2}a\cdot\sin\cfrac{\pi}{3}=\cfrac{\sqrt{3}}{4} a \in\left(\cfrac{\sqrt{3}}{8}, \cfrac{\sqrt{3}}{2}\right)\)
解后感悟:①任意三角形的刻画:\(a+b>c\)且\(a+c>b\)且\(b+c>a\);此时不需要两边差的刻画;
②锐角三角形 用角刻画:\(A,B,C\in (0,\cfrac{\pi}{2})\);
用边刻画:\(a^2+b^2>c^2\)且\(a^2+c^2>b^2\)且\(b^2+c^2>a^2\);
[法2]:结合已知条件,从角的角度思考和刻画,转化为关于角的三角函数求解;
由于\(B=\cfrac{\pi}{3}\),故\(A+C=\cfrac{2\pi}{3}\),则有\(A=\cfrac{2\pi}{3}-C\);
又由于锐角三角形的限制,则\(\left\{\begin{array}{l}{0<C<\cfrac{\pi}{2}}\\{0<\cfrac{2\pi}{3}-C<\cfrac{\pi}{2}}\end{array}\right.\),解得\(\cfrac{\pi}{6}<C<\cfrac{\pi}{2}\)
又应用正弦定理\(\cfrac{a}{\sin A}=\cfrac{c}{\sin C}\),又已知\(c=1\),得到\(a=\cfrac{c\sin A}{\sin C}=\cfrac{\sin A}{\sin C}\),
则由三角形面积公式得到,
\(S_{\triangle ABC}=\cfrac{1}{2}a\cdot c\cdot\sin B=\cfrac{1}{2}\cdot a\cdot\sin B\)
\(=\cfrac{1}{2}\times\cfrac{\sin A}{\sin C}\times\sin B\)\(=\cfrac{\sqrt{3}}{4}\times \cfrac{\sin A}{\sin C}\)
\(=\cfrac{\sqrt{3}}{4}\times\cfrac{\sin(\cfrac{2\pi}{3}-C)}{\sin C}=\cfrac{\sqrt{3}}{4}\times\cfrac{\cfrac{\sqrt{3}}{2}\cos C+\cfrac{1}{2}\sin C}{\sin C}\)
\(=\cfrac{3}{8}\cdot \cfrac{1}{\tan C}+\cfrac{\sqrt{3}}{8}\)
由于\(\cfrac{\pi}{6}<C<\cfrac{\pi}{2}\),\(y=\tan C\)单调递增,故\(\cfrac{\sqrt{3}}{3}<\tan C<+\infty\),
则有\(0<\cfrac{1}{\tan C}<\sqrt{3}\),则\(0<\cfrac{3}{8}\cdot \cfrac{1}{\tan C}<\cfrac{3\sqrt{3}}{8}\),
则有\(0+\cfrac{\sqrt{3}}{8}<\cfrac{3}{8}\cdot\cfrac{1}{\tan C}+\cfrac{\sqrt{3}}{8}<\cfrac{3\sqrt{3}}{8}+\cfrac{\sqrt{3}}{8}\),
即\(\cfrac{\sqrt{3}}{8}<\cfrac{3}{8}\cdot \cfrac{1}{\tan C}+\cfrac{\sqrt{3}}{8}<\cfrac{\sqrt{3}}{2}\),
故\(\cfrac{\sqrt{3}}{8}<S_{\triangle ABC}<\cfrac{\sqrt{3}}{2}\),即所求三角形面积的取值范围为\(\left(\cfrac{\sqrt{3}}{8}, \cfrac{\sqrt{3}}{2}\right)\)
法1:由于\(AB:AC=2:1\),则由三角形的内角平分线定理可知\(BD:DC=2:1\),
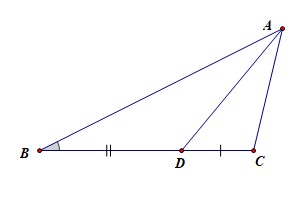
则\(S_{\triangle ABD}=\cfrac{2}{3}S_{\triangle ABC}=\cfrac{2}{3}\times \cfrac{1}{2}\times 2\times1 \times sinA=\cfrac{2}{3}sinA\leq \cfrac{2}{3}\),
当且仅当\(sinA=1\)时,即\(\angle A=\cfrac{\pi}{2}\)时,\(S_{\triangle ABD}\)面积最大,为\(\cfrac{2}{3}\),故选\(B\);
法2:利用图形求解;说明:要求面积的最大值,则需要高度最大,
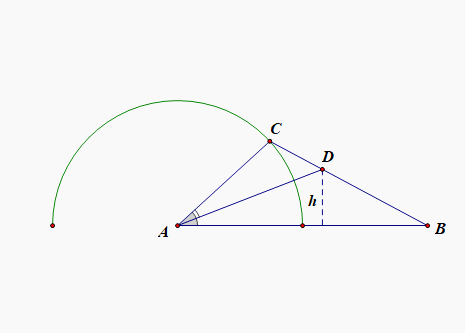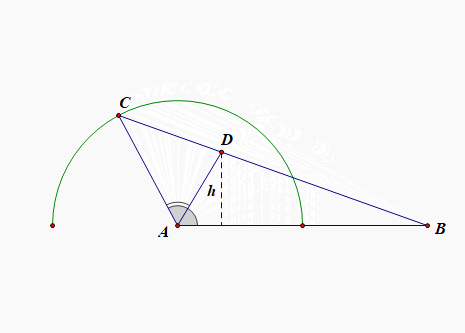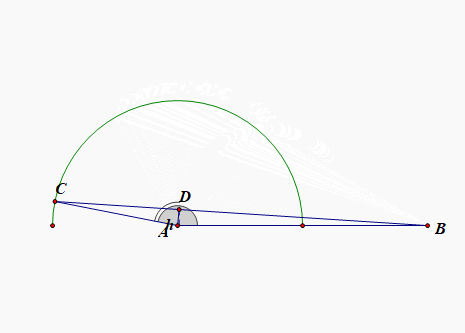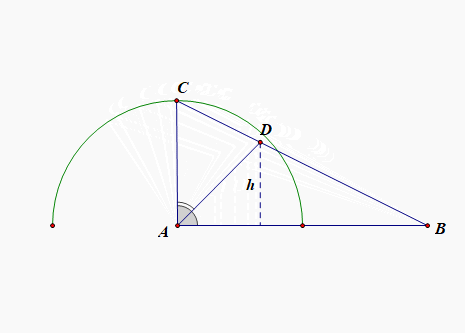
如图所示,三角形的底边为\(AB=2\)为定值,则高度最大时,面积最大,
由于\(AC=1\)为定值,相当于点\(C\)在半圆上运动,很显然当\(\angle A=\cfrac{\pi}{2}\)时,\(\triangle ABD\)的高\(h\)最大,
由三角形相似可知,此时\(h=\cfrac{2}{3}\),故\(S_{\triangle ABD}=\cfrac{1}{2}\times 2\times \cfrac{2}{3}=\cfrac{2}{3}\),故选\(B\);
法3:如下图所示,由于\(AB:AC=2:1\),则由三角形的内角平分线定理可知\(BD:DC=2:1\),令\(BD=2k\),\(DC=k(k>0)\),
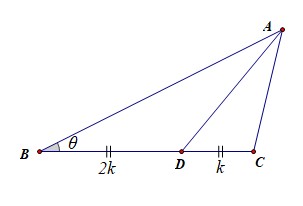
则\(cos\theta=\cfrac{2^2+(3k)^2-1^2}{2\times 2\times 3k}=\cfrac{3k^2-1}{4k}\),
则\(sin\theta=\sqrt{1-(\cfrac{3k^2-1}{4k})^2}=\sqrt{\cfrac{-9k^4+10k^2-1}{16k^2}}\),
则\(S_{\triangle ABD}=\cfrac{1}{2}\times 2\times 2k\times sin\theta\)
\(=2\times \sqrt{k^2\times \cfrac{-9k^4+10k^2-1}{16k^2}}=2\sqrt{\cfrac{-9k^4+10k^2-1}{16}}\),
令\(f(k)=-9k^4+10k^2-1\),则\(f'(k)=-36k^3+20k=-k(36k^2-20)\),
令\(f'(k)=0\),得到\(k=0\)(舍去)或\(k=-\cfrac{\sqrt{5}}{3}\)(舍去),或\(k=\cfrac{\sqrt{5}}{3}\),
由穿根法得到其大致图像可知,
\(f(k)\)在区间\((0,\cfrac{\sqrt{5}}{3})\)上单调递增,在区间\((\cfrac{\sqrt{5}}{3},+\infty)\)上单调递减,
故\(f(k)_{max}=f(\cfrac{\sqrt{5}}{3})=\cfrac{16}{9}\),
故面积的最大值为\(S_{\triangle ABD}=2\sqrt{\cfrac{-9k^4+10k^2-1}{16}}=2\sqrt{\cfrac{\frac{16}{9}}{16}}=\cfrac{2}{3}\). 故选\(B\);
解后感悟:各位同学,如果能看到这里,估计你也能体会到导数的强大功能了吧。
(1).求角\(A\).
分析:由已知\(\vec{m}//\vec{n}\),可得到\(a\cos C+\sqrt{3}a\sin C-b-c=0\),
由正弦定理边化角可得,\(\sin A\cos C+\sqrt{3}\sin A\sin C-\sin B-\sin C=0\),
由于\(B=\pi-A-C\),则有\(\sin A\cos C+\sqrt{3}\sin A\sin C-\sin(A+C)-\sin C=0\),
整理得到,\(\sqrt{3}\sin A\sin C-\cos A\sin C-\sin C=0\),
由于\(\sin C\neq 0\),则得到\(\sqrt{3}\sin A-\cos A-1=0\),
由辅助角公式可得,\(2\sin(A-\cfrac{\pi}{6})=1\),
即\(\sin(A-\cfrac{\pi}{6})=\cfrac{1}{2}\),
由\(0<A<\cfrac{\pi}{2}\),则\(-\cfrac{\pi}{6}<A-\cfrac{\pi}{6}<\cfrac{\pi}{3}\),
则\(A-\cfrac{\pi}{6}=\cfrac{\pi}{6}\),故\(A=\cfrac{\pi}{3}\).
(2).若\(a=3\),求\(\triangle ABC\)面积的取值范围。
分析: 由\(\cfrac{b}{\sin B}=\cfrac{c}{\sin C}=\cfrac{a}{\sin A}=\cfrac{3}{\frac{\sqrt{3}}{2}}=2\sqrt{3}\),
则得\(b=2\sqrt{3}\sin B\), \(c=2\sqrt{3}\sin C\),\(C=\cfrac{2\pi}{3}-B\),
所以\(bc=12\sin B\sin C=12\sin B\sin(\cfrac{2\pi}{3}-B)=12\sin B\sin(\cfrac{\pi}{3}+B)\)
\(=12\sin B(\cfrac{\sqrt{3}}{2}\cdot \cos B+\cfrac{1}{2}\cdot\sin B)=6\sqrt{3}\sin B\cos B+6\sin^2B\)
\(=3\sqrt{3}\sin2B+3(1-\cos2B)=3\sqrt{3}\sin2B-3\cos2B+3\)
\(=6(\cfrac{\sqrt{3}}{2}\sin2B-\cfrac{1}{2}\cos2B)+3=6\sin(2B-\cfrac{\pi}{6})+3\)
由于\(\triangle ABC\)为锐角三角形,所以\(\left\{\begin{array}{l}0<B<\cfrac{\pi}{2}\\ 0<\cfrac{2 \pi}{3}-B<\cfrac{\pi}{2}\end{array}\right.\), 解得\(\cfrac{\pi}{6}<B<\cfrac{\pi}{2}\)
所以\(\cfrac{\pi}{6}<2B-\cfrac{\pi}{6}<\cfrac{5\pi}{6}\),\(\cfrac{1}{2}<\sin(2B-\cfrac{\pi}{6})\leqslant 1\),
故\(6<6\sin(2B-\cfrac{\pi}{6})+3\leqslant 9\),即\(6<bc\leqslant9\)
又由于\(S_{\triangle_{ABC}}=\cfrac{1}{2}bc\sin A=\cfrac{\sqrt{3}}{4}bc\)
故\(\cfrac{3\sqrt{3}}{2}<\cfrac{\sqrt{3}}{4}bc\leqslant \cfrac{9\sqrt{3}}{4}\)
所以, \(\triangle ABC\)面积的取值范围为\((\cfrac{3\sqrt{3}}{2}, \cfrac{9\sqrt{3}}{4}]\).
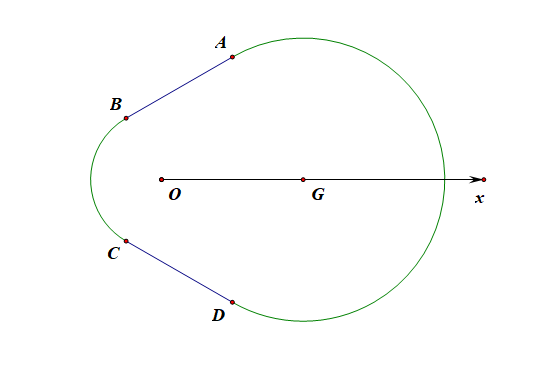
在极坐标系 \(Ox\) 中 \(A(2, \cfrac{\pi}{3})\), \(B(1, \cfrac{2\pi}{3})\), \(C(1,\cfrac{4\pi}{3})\), \(D(2,-\cfrac{\pi}{3})\), 弧 \(BC\), \(AD\) 所在圆的圆心分别是 \((0,0)\), \((2,0),\) 曲线 \(M_{1}\) 是弧 \(BC\), 曲线\(M_{2}\) 是弧 \(AD\).
(1). 分别写出 \(M_{1}\), \(M_{2}\) 的极坐标方程;
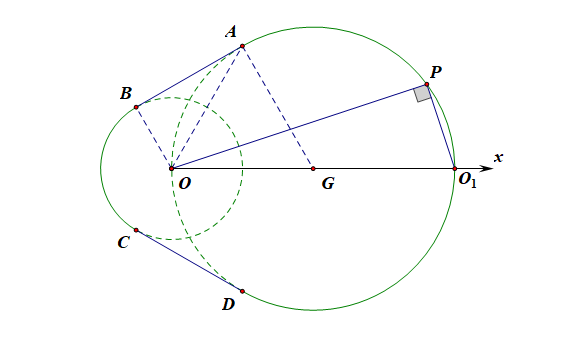
解析:如图所示,由题意可知, \(M_1\)的极坐标方程为 \(\rho=1\),(\(\cfrac{2\pi}{3}\leqslant\theta\leqslant\cfrac{4\pi}{3}\)),
而圆弧 \(AD\) 所在圆的圆心为 \((2,0)\),设 \(P(\rho,\theta)\) 为 \(M_2\) 上任意一点,
则在\(\triangle OO_1P\)中,由 \(\cos\theta=\cfrac{\rho}{4}\) 可得, \(\rho=4\cos\theta\),(\(-\cfrac{\pi}{3}\leqslant\theta\leqslant\cfrac{\pi}{3}\)),
故 \(M_{1}\), \(M_{2}\) 的极坐标方程分别为:
\(\rho=1\)(\(\cfrac{2\pi}{3}\leqslant\theta\leqslant\cfrac{4\pi}{3}\)) 和 \(\rho=4\cos\theta\)(\(-\cfrac{\pi}{3}\leqslant\theta\leqslant\cfrac{\pi}{3}\)).
(2). 点 \(E\), \(F\) 位于曲线 \(M_{2}\) 上, 且 \(\angle EOF=\cfrac{\pi}{3}\), 求 \(\triangle EOF\) 面积的取值范围.
解析:不妨设 \(E(\rho_{1}, \alpha)\), \(F(\rho_{2}, \alpha-\cfrac{\pi}{3})\)可以设点\(F\) 的辅角为\(\beta\),此时\(\beta\)为负角,则由题目可知,\(\alpha-\beta=\cfrac{\pi}{3}\)[此处还可以借助数轴上任意两点的距离公式\(|AB|\)\(=\)\(x_{_{A}}\)\(-\)\(x_{_{B}}\)来理解],故解得\(\beta=\alpha-\cfrac{\pi}{3}\)\(\quad\),其中 \(0\leqslant \alpha\leqslant\cfrac{\pi}{3}\),
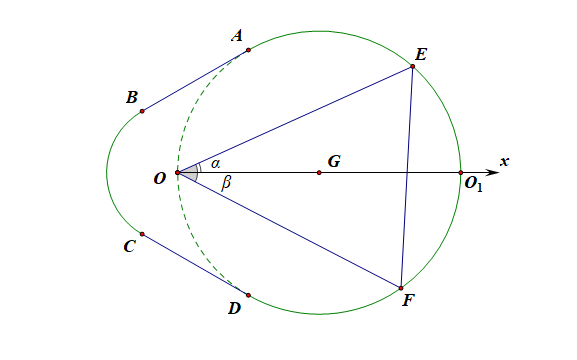
则 \(\rho_{1}=4\cos\alpha\), \(\rho_{2}=4\cos(\alpha-\cfrac{\pi}{3})\),则有
\(S_{\Delta EOF}=\cfrac{1}{2}\rho_{1}\cdot\rho_{2}\cdot\sin\cfrac{\pi}{3}\)\(=\)\(4\sqrt{3}\cdot\cos\alpha(\cos\alpha\cos\cfrac{\pi}{3}+\sin\alpha\sin\cfrac{\pi}{3})\)
\(=4\sqrt{3}(\cfrac{1}{2}\cos^{2}\alpha+\cfrac{\sqrt{3}}{2}\cos\alpha\cdot\sin\alpha)=2\sqrt{3}\sin(2\alpha+\cfrac{\pi}{6})+\sqrt{3}\)
又由于 \(0 \leqslant \alpha \leqslant \cfrac{\pi}{3}\), \(\cfrac{1}{2}\leqslant\sin(2\alpha+\cfrac{\pi}{6})\leqslant 1\),
则 \(2\sqrt{3}\leqslant 2\sqrt{3}\sin(2\alpha+\cfrac{\pi}{6})+\sqrt{3}\leqslant 3\sqrt{3}\),
所以 \(\triangle EOF\) 的面积的取值范围是 \([2\sqrt{3}, 3\sqrt{3}]\) .
法1:做出如下的图形,由图形可以看出,当圆上的动点到直线的距离最大时,\(\triangle ABP\)面积最大,当当圆上的动点到直线的距离最小时,\(\triangle ABP\)面积最小,
故三角形的高的最大值为\(2\sqrt{2}+r=2\sqrt{2}+\sqrt{2}=3\sqrt{2}\);三角形的高的最小值为\(2\sqrt{2}-r=2\sqrt{2}-\sqrt{2}=\sqrt{2}\);又\(|AB|=2\sqrt{2}\),
故\([S_{\triangle ABP}]_{max}=\cfrac{1}{2}\times 3\sqrt{2}\times 2\sqrt{2}=6\),\([S_{\triangle ABP}]_{min}=\cfrac{1}{2}\times \sqrt{2}\times 2\sqrt{2}=2\),故选\(A\)。
法2:设圆上任一点的坐标为\(P(2+\sqrt{2}cos\theta,\sqrt{2}sin\theta)\),则三角形的高为\(h=d=\cfrac{|2+\sqrt{2}cos\theta+\sqrt{2}sin\theta+2|}{\sqrt{2}}=\cfrac{|4+2sin(\theta+\cfrac{\pi}{4})|}{\sqrt{2}}\)
故当\(sin(\theta+\cfrac{\pi}{4})=1\)时,\(h_{max}=\cfrac{6}{\sqrt{2}}=3\sqrt{2}\),
当\(sin(\theta+\cfrac{\pi}{4})=-1\)时,\(h_{min}=\cfrac{2}{\sqrt{2}}=\sqrt{2}\),又\(|AB|=2\sqrt{2}\),
故\([S_{\triangle ABP}]_{max}=\cfrac{1}{2}\times 3\sqrt{2}\times 2\sqrt{2}=6\),\([S_{\triangle ABP}]_{min}=\cfrac{1}{2}\times \sqrt{2}\times 2\sqrt{2}=2\),故选\(A\)。
法1:做出如下的示意图,设直线\(AB\)的斜率为\(k\),不妨只考虑\(k>0\),则\(AB:y=k(x-4)\),即\(kx-y-4k=0\);
将直线和抛物线方程联立,消去\(x\)得到,\(ky^2-4y-16k=0\),则\(y_1+y_2=-\cfrac{-4}{k}=\cfrac{4}{k}\),\(y_1y_2=-16\),
则\(|AB|=\sqrt{1+\cfrac{1}{k^2}}|y_1-y_2|=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(y_1+y_2)^2-4y_1y_2}\)
\(=\sqrt{1+\cfrac{1}{k^2}}\sqrt{(\cfrac{4}{k})^2-4\times (-16)}=\sqrt{\cfrac{k^2+1}{k^2}}\cdot 4\cdot \sqrt{\cfrac{4k^2+1}{k^2}}\)
\(=4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\),
又点\(F\)到直线\(AB\)的距离为\(d=h=\cfrac{|3k|}{\sqrt{k^2+1}}=\cfrac{3k}{\sqrt{k^2+1}}\),
则\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 4\cdot \cfrac{\sqrt{k^2+1}\cdot \sqrt{4k^2+1}}{k^2}\cdot \cfrac{3k}{\sqrt{k^2+1}}\)
\(=6\times \cfrac{\sqrt{4k^2+1}}{k}=6\times \sqrt{4+\cfrac{1}{k^2}}\),
当\(k\rightarrow \infty\)时,所求面积有最小值,\(S_{min}=6\times 2=12\)。故选\(B\).
法2:仿上利用均值不等式可以说明,当\(AB\)和\(x\)轴垂直时,\(S_{\triangle ABF}\)有最小值;
\(S_{\triangle ABF}=\cfrac{1}{2}\cdot 3\cdot (|y_1|+|y_2|)\ge \cfrac{3}{2}\cdot 2\sqrt{|y_1y_2|}= \cfrac{3}{2}\cdot 2\cdot 4=12\),故选\(B\).
分析:边化角,由\(asinA-csinC=(\sqrt{2}a-b)sinB\)得到,\(a^2+b^2-c^2=\sqrt{2}ab\),则可知\(cosC=\cfrac{\sqrt{2}}{2}\),又\(C\in (0,\pi)\),则\(C=\cfrac{\pi}{4}\);
如图所示,弧\(AB\)所对的圆心角\(\angle C\)为定值,当其在圆上运动时,只有当其落在点\(D\)时面积最大(底边不动,高线最大),此时\(\triangle ABC\)为顶角为\(C=45^{\circ}\)的等腰三角形,\(\angle A=\angle B=\cfrac{135^{\circ}}{2}\),
则当\(a=b\)时\([S_{\triangle ABC}]_{max}=\cfrac{1}{2}absinC=2(\sqrt{2}+1)\),解得\(a^2=8+4\sqrt{2}\),
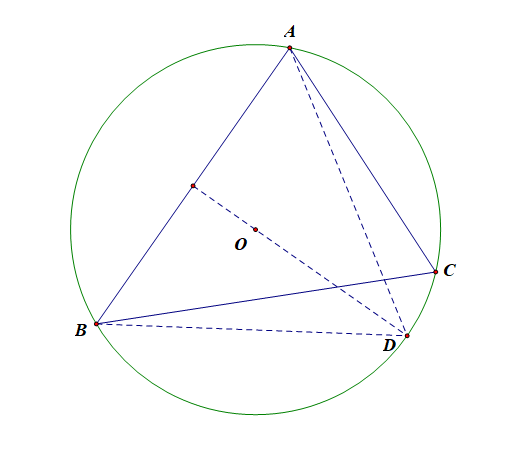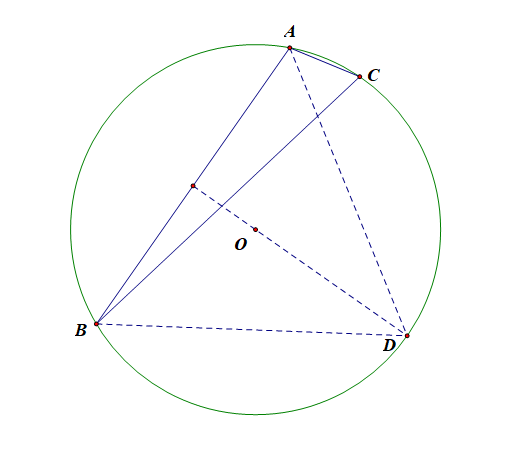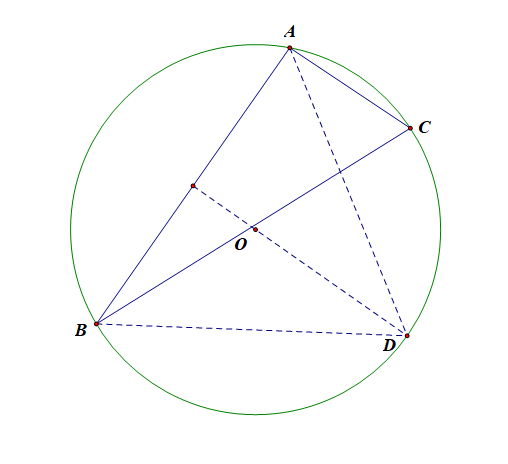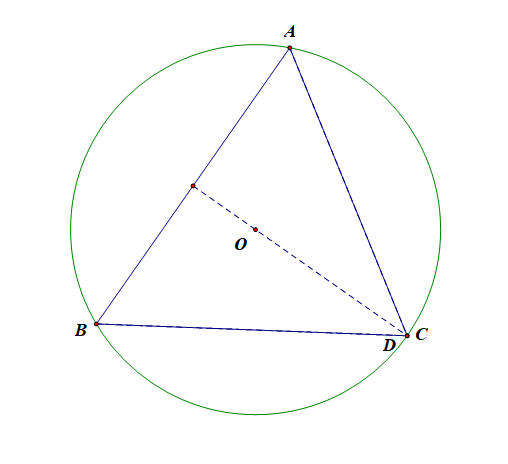
则由\(\cfrac{a}{sinA}=2R\)得到,\(4R^2=\cfrac{a^2}{sin^2A}=\cfrac{a^2}{sin^2\frac{135^{\circ}}{2}}=\cfrac{8+4\sqrt{2}}{\frac{1}{2}(1+\frac{\sqrt{2}}{2})}=16\),则\(R=2\)。故选\(D\).
(1).\(M\)为曲线\(C_1\)上的动点,点\(P\)在线段\(OM\)上,且满足\(|OM|\cdot|OP|=16\),求点\(P\)的轨迹\(C_2\)的直角坐标方程;
【法一】:学生容易想到的解法,也是我们交给学生的方法。
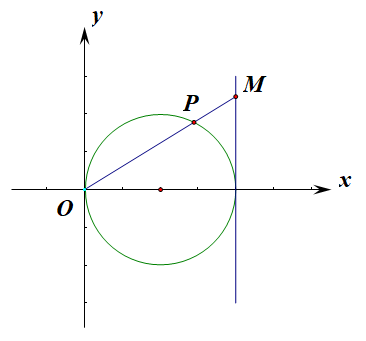
容易化简\(C_1:x=4\),做出简单的示意图,我们可以令\(M(4,m)、P(x,y)\),
则由题目可知\(\cfrac{y}{x}=\cfrac{m}{4}\),即\(m=\cfrac{4y}{x}\),
又由题目可知满足条件\(|OM|\cdot|OP|=16\),即\(\sqrt{4^2+m^2}\cdot\sqrt{x^2+y^2}=16\),
将\(m=\cfrac{4y}{x}\)代入,整理得到\((4^2+\cfrac{16y^2}{x^2})\cdot(x^2+y^2)=256\),
整理得到\(x^4+2x^2y^2-16x^2+y^4=0\),即\(x^4+2x^2y^2+y^4=16x^2\),
即\((x^2+y^2)^2=(4x)^2\),两边开方得到\(x^2+y^2=4x\)[此处由于\(x\)为非负值,故舍去\(x^2+y^2=-4x\)],
最终可以化简为\((x-2)^2+y^2=4(x>0)\)。
【法2】:直接借助极坐标系来思考运算,令\(M(\rho,\theta)\),\(P(\rho_1,\theta)(\rho_1>0)\),由题可知,
点M满足\(C_1\)的方程\(\rho cos\theta=4\) 。则\(\rho=\cfrac{4}{cos\theta}\),
又\(|OM|=\rho=\cfrac{4}{cos\theta}\),\(|OP|=\rho_1\),又由题目可知\(|OM|\cdot|OP|=\rho\rho_1=16\),
故\(\rho_1=\cfrac{16}{\rho}=4cos\theta(\rho_1>0)\),两边同乘以\(\rho_1\)得到
\(\rho_1^2=4\rho_1 cos\theta\),转化为直角坐标方程为\(x^2+y^2=4x(x\neq 0)\),
即\((x-2)^2+y^2=4(x\neq 0)\)为曲线\(C_2\)的直角坐标方程。
解后反思:
①法1的代数式变形,许多学生根本想不到;
②结题中限制\(x\neq 0\)是为了和上述的\(\rho_1>0\)对应。
③此题目的法2的解答提醒我们,若题目中出现了经过极点的两个线段的四则运算的条件,那么采用极坐标思考和运算应该是比较简单和快捷的,故我们必须扭转以直角坐标为桥梁的的求解思路,快速适应在极坐标系下的思维模式。
(2).设点\(A\)的极坐标为\((2,\cfrac{\pi}{3})\),点\(B\)在曲线\(C_2\)上,求\(\Delta OAB\)面积的最大值.
【法1】:直接借助平面几何的形来思考运算,结合运动观点和特殊化策略;让点\(B\)在圆上跑一圈即可看出思路;
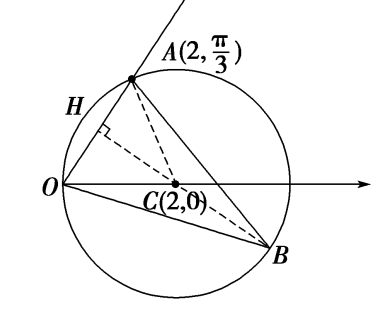
连接\(AC\) ,易知\(\Delta AOC\)为正三角形,底边\(|OA|\)为定值,则当高线最大时,\(S_{\Delta AOB}\)面积最大,
如图所示,过圆心\(C\)做\(AO\)的垂线,交\(AO\)于\(H\),交圆\(C\)于点\(B\),此时\(S_{\Delta AOB}\)面积最大,
\(S_{max}=\cfrac{1}{2}\cdot |AO||HB|=\cfrac{1}{2}\cdot |AO|(|HC|+|BC|)=2+\sqrt{3}\)。
【法2】:借助圆的参数方程和点线距公式求解;
直线\(OA\)的方程为\(\sqrt{3}x-y=0\),点\(B\)在曲线\(C_2\)上,
故点\(B\)的参数坐标为\((2cos\theta+2,2sin\theta)\)\((\theta\in (-\pi,\pi))\),
故三角形\(\Delta OAB\)的一条边\(OA\)上的高为点\(B\)到直线\(OA\)的距离为\(h_{OA}\),
\(h_{OA}=\cfrac{|\sqrt{3}(2cos\theta+2)-2sin\theta|}{\sqrt{(\sqrt{3})^2+1^2}}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|\)
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA|\cdot h_{OA}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|=|2cos(\theta+\cfrac{\pi}{6})+\sqrt{3}|\),
当\(cos(\theta+\cfrac{\pi}{6})=1\),即\(\theta=-\cfrac{\pi}{6}\)时,\(S_{max}=2+\sqrt{3}\)。
【法3】:直接借助极坐标系来思考运算,利用\(S_{\triangle}=\cfrac{1}{2}absinC\)求解;
点\(A(2,\cfrac{\pi}{3})\),点\(B(\rho,\alpha)(\alpha\in (-\cfrac{\pi}{2},\cfrac{\pi}{2}))\),又点\(B\)满足曲线\(C_2\)的极坐标方程,
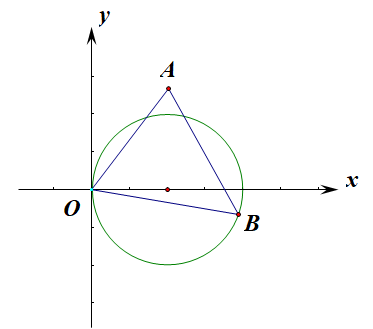
故\(|OB|=\rho=4cos\alpha\),\(\angle AOB=\cfrac{\pi}{3}-\alpha\),
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA||OB|sin\angle AOB=\cfrac{1}{2}\cdot 2\cdot 4cos\alpha\cdot sin(\cfrac{\pi}{3}-\alpha)\)
\(=4cos\alpha \cdot sin(\cfrac{\pi}{3}-\alpha)=4cos\alpha\cdot(\cfrac{\sqrt{3}}{2}cos\alpha-\cfrac{1}{2}sin\alpha)\)
\(=2\sqrt{3}cos^2\alpha-2sin\alpha\cdot cos\alpha=\sqrt{3}\cdot (1+cos2\alpha)-sin2\alpha=-2sin(2\alpha-\cfrac{\pi}{3})+\sqrt{3}\),
故当\(2\alpha-\cfrac{\pi}{3}=-\cfrac{\pi}{2}\),即\(\alpha=-\cfrac{\pi}{12}\)时,\(S_{\Delta OAB}\)取到最大值\(2+\sqrt{3}\)。
[引申探究]
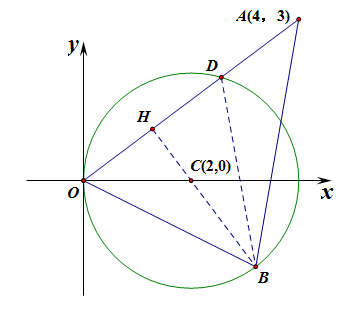
- 当点\(A\)在圆外时,如点\(A(4,3)\),又该如何思考呢?
分析:连接\(OA\),和圆相交于点\(D\),过点\(C\)做弦\(OD\)的中垂线,和弦\(OD\)相交于点\(H\),和圆相交于点\(B\),
则此时点\(B\)到底边\(OA\)的距离最大,故此时的\(S_{\Delta AOB}\)面积最大,
具体\(S_{\Delta AOB}\)面积最大时的求法如下,
底边长\(|OA|\)固定不变,高线\(|BH|=|BC|+|HC|\),其中\(|BC|\)长为半径,题目给定,
\(|HC|\)可以用点\(C(2,0)\)到直线\(OA\)的距离公式求得,或利用\(Rt\Delta OCH\)求解即可,
故面积的最大值可解;
- 当点\(A\)在圆内时,如点\(A(3,1)\),又该如何思考呢?
分析:连接\(OA\)并延长和圆相交于点\(D\),
过点\(C\)做弦\(OD\)的中垂线,和弦\(OD\)相交于点\(H\),和圆相交于点\(B\),
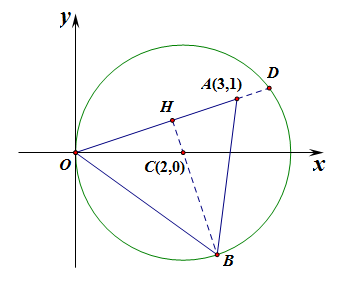
则此时点\(B\)到底边\(OA\)的距离最大,故此时的\(S_{\Delta AOB}\)面积最大,
具体\(S_{\Delta AOB}\)面积最大时的求法如下,底边长\(|OA|\)固定不变,高线\(|BH|=|BC|+|HC|\),
其中\(|BC|\)长为半径,题目给定,\(|HC|\)可以用点\(C(2,0)\)到直线\(OA\)的距离公式求得,
或利用\(Rt\Delta OCH\)求解即可,故面积的最大值可解;
法2:直线\(OA\)的方程为\(\sqrt{3}x-y=0\),点\(B\)在曲线\(C_2\)上,故点B的参数坐标为\((2cos\theta+2,2sin\theta)\)\((\theta\in (-\pi,\pi))\),
(?此处怎么转化,为什么这样转化)
故三角形\(\Delta OAB\)的一条边\(OA\)上的高为点\(B\)到直线\(OA\)的距离
\(h_{OA}=\cfrac{|\sqrt{3}(2cos\theta+2)-2sin\theta|}{\sqrt{(\sqrt{3})^2+1^2}}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|\)
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA|\cdot h_{OA}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|=|2cos(\theta+\cfrac{\pi}{6})+\sqrt{3}|\),
当\(cos(\theta+\cfrac{\pi}{6})=1\),即\(\theta=-\cfrac{\pi}{6}\)时,\(S_{max}=2+\sqrt{3}\)。
法3:直接借助极坐标系来思考运算,
点\(A(2,\cfrac{\pi}{3})\),点\(B(\rho,\alpha)(\alpha\in (-\cfrac{\pi}{2},\cfrac{\pi}{2}))\),
又点B满足曲线\(C_2\)的极坐标方程,

故\(|OB|=\rho=4cos\alpha\),\(\angle AOB=\cfrac{\pi}{3}-\alpha\),
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA||OB|sin\angle AOB=\cfrac{1}{2}\cdot 2\cdot 4cos\alpha\cdot sin(\cfrac{\pi}{3}-\alpha)\)
\(=4cos\alpha \cdot sin(\cfrac{\pi}{3}-\alpha)=4cos\alpha\cdot(\cfrac{\sqrt{3}}{2}cos\alpha-\cfrac{1}{2}sin\alpha)\)
\(=2\sqrt{3}cos^2\alpha-2sin\alpha\cdot cos\alpha=\sqrt{3}\cdot (1+cos2\alpha)-sin2\alpha=-2sin(2\alpha-\cfrac{\pi}{3})+\sqrt{3}\),
故当\(2\alpha-\cfrac{\pi}{3}=-\cfrac{\pi}{2}\),即\(\alpha=-\cfrac{\pi}{12}\)时,\(S_{\Delta OAB}\)取到最大值\(2+\sqrt{3}\)。
分析:由\(cos2(B+C)=cos(2B+2C)=cos(2\pi-2A)=cos2A\),
将已知等式变形为\(2\cdot 2cos^2\cfrac{A}{2}-cos2A=\cfrac{7}{2}\),
即\(2(1+cosA)-cos2A=\cfrac{7}{2}\),
即\(2(1+cosA)-(2cos^2A-1)=\cfrac{7}{2}\),
化简为\(4cos^2A-4cosA+1=(2cosA-1)^2=0\),
解得\(cosA=\cfrac{1}{2},A\in(0,\pi)\),故\(A=\cfrac{\pi}{3}\),
到此题目转化为已知\(A=\cfrac{\pi}{3},a=2\),求\(\Delta ABC\)的面积的最大值。
接下来有两个思路途径:
思路一:使用均值不等式,由余弦定理\(a^2=b^2+c^2-2bccosA,A=\cfrac{\pi}{3},a=2\)
得到\(b^2+c^2=4+bc\ge 2bc\),解得\(bc\leq 4(当且仅当b=c=2时取到等号)\),
则\(S_{\Delta ABC}=\cfrac{1}{2}bcsinA \leq \cfrac{\sqrt{3}}{4}\times 4=\sqrt{3}\)。
即三角形面积的最大值是\(\sqrt{3}\)。
法2:由于题目已知\(A=\cfrac{\pi}{3},a=2\),则\(B+C=\cfrac{2\pi}{3}\),故\(B,C\in (0,\cfrac{2\pi}{3})\),
则由正弦定理得\(\cfrac{b}{sinB}=\cfrac{c}{sinC} =\cfrac{a}{sinA} =\cfrac{2}{\frac{\sqrt{3}}{2}} =\cfrac{4\sqrt{3}}{3}\),
则\(b=\cfrac{4\sqrt{3}}{3}sinB\),\(c=\cfrac{4\sqrt{3}}{3}sinC\),
则\(bc=(\cfrac{4\sqrt{3}}{3})^2\cdot sinB\cdot sinC=\cfrac{16}{3}sinB\cdot sin(\cfrac{2\pi}{3}-B)\)
\(=\cfrac{16}{3}sinB\cdot (\cfrac{\sqrt{3}}{2}cosB+\cfrac{1}{2}sinB)\)
\(=\cfrac{16}{3}[\cfrac{\sqrt{3}}{2}sinB\cdot cosB+\cfrac{1}{2}sin^2B]\)
\(=\cfrac{16}{3}[\cfrac{\sqrt{3}}{4}sin2B+\cfrac{1}{4}(1-cos2B)]\)
\(=\cfrac{16}{3}(\cfrac{\sqrt{3}}{4}sin2B-\cfrac{1}{4}cos2B+\cfrac{1}{4})\)
\(=\cfrac{8}{3}(sin2B\cdot \cfrac{\sqrt{3}}{2}-cos2B\cdot \cfrac{1}{2})+\cfrac{4}{3}\)
\(=\cfrac{8}{3}sin(2B-\cfrac{\pi}{6})+\cfrac{4}{3}\)
当\(2B-\cfrac{\pi}{6}=\cfrac{\pi}{2}\),即\(B=\cfrac{5\pi}{12} \in(0,\cfrac{2\pi}{3})\)时,\(sin(2B-\cfrac{\pi}{6})=1\),
即\(bc_{max}=\cfrac{8}{3}+\cfrac{4}{3}=4\)
故\([S_{\Delta}]_{max}=\cfrac{1}{2}bcsinA\leq \cfrac{\sqrt{3}}{4}\times 4=\sqrt{3}\)。
分析:由\(\cfrac{b}{a}=\cfrac{sinB}{sinA}=\cfrac{1-cosB}{cosA}\),
得到\(sinBcosA+cosBsinA=sinA\),即\(sin(A+B)=sinA\)
则\(sinC=sinA\),即\(A=C\),
故\(a=b=c\),为等边三角形。
在\(\Delta AOB\)中,\(AB^2=2^2+1^2-2\cdot 2\cdot 1\cdot cos\theta=5-4cos\theta\),
故\(S_{OACB}=S_{\Delta AOB}+S_{\Delta ABC}\)
\(=\cfrac{1}{2}\cdot 2\cdot 1\cdot sin\theta+\cfrac{\sqrt{3}}{4}\cdot AB^2\)
\(=sin\theta+\cfrac{\sqrt{3}}{4}(5-4cos\theta)=2sin(\theta-\cfrac{\pi}{3})+\cfrac{5\sqrt{3}}{4}\)
当\(\theta-\cfrac{\pi}{3}=\cfrac{\pi}{2}\)时,即\(\theta=\cfrac{5\pi}{6}\in (0,\pi)\)时,四边形的面积有最大值,
且\(S_{max}=2+\cfrac{5\sqrt{3}}{4}=\cfrac{8+5\sqrt{3}}{4}\),故选\(B\)。
分析:当\(C\)取到最大值时,\(cosC\)取得最小值,故先研究\(cosC\),
\(cosC=\cfrac{a^2+b^2-c^2}{2ab}=\cfrac{3c^2+1}{4c}\)
\(=\cfrac{1}{4}(3c+\cfrac{1}{c})\ge \cfrac{1}{4}\cdot 2\sqrt{3}=\cfrac{\sqrt{3}}{2}\),
当且仅当\(3c=\cfrac{1}{c}\),即\(c=\cfrac{\sqrt{3}}{3}\)时取得等号;
且此时\(sinC=\cfrac{1}{2}\),故当\(C\)取到最大值时,
\(S_{\Delta ABC}=\cfrac{1}{2}absinC\)\(=\cfrac{1}{2}\cdot 2c\cdot 1\cdot \cfrac{1}{2}=\cfrac{\sqrt{3}}{6}\),故选\(B\)。
(1). 求曲线 \(C_{1}\) 的普通方程与曲线 \(C_{2}\) 的直角坐标方程;
解: 曲线 \(C_{1}\) 的参数方程为 \(\left\{\begin{array}{l}x=3+3\cos\alpha,\\y=3\sin\alpha\end{array}\right.\) ( \(\alpha\) 为参数),
转换为直角坐标方程为 \((x-3)^{2}+y^{2}=9\).
曲线 \(C_{2}\) 的极坐标方程为 \(\rho+4\cos\theta=0\), 转换为直角坐标方程为\(x^{2}+y^{2}+4x=0\).
(2).设点 \(A\),\(B\) 分别是曲线 \(C_{1}\), \(C_{2}\) 上的两个动点,且 \(\angle AOB=\cfrac{\pi}{2}\),求 \(\triangle AOB\) 面积的最大值.
解: 此处有个值得思考的好问题,为什么使用极坐标系来求解而不用直角坐标系?
由(1)得:曲线 \(C_{1}\) 的极坐标方程为 \(\rho=6\cos\theta\),
曲线 \(C_{2}\) 的极坐标方程为 \(\rho=-4\cos\theta\),
设 \(A(\rho_{1}, \theta)\), \(B(\rho_{2}, \theta+\cfrac{\pi}{2})\),
所以 \(S_{\triangle AOB}=\cfrac{1}{2}\times OA\times OB\times \sin\angle AOB=\cfrac{1}{2}\times\rho_{1}\times \rho_{2}\times \sin\cfrac{\pi}{2}\)
\(=\cfrac{1}{2}\times 6\cos\theta\times [-4\cos(\theta+\cfrac{\pi}{2})]\),
\(=\cfrac{1}{2}\times 6\cos\theta\times 4\sin\theta=12\sin\theta\cos\theta=6\sin2\theta\leqslant 6\),
当 \(\theta=\cfrac{\pi}{4}\) 时, \(\triangle AOB\) 面积的最大值为 \(6\).
解后反思:本题目的求解,若改用平面直角坐标系,运算量会比较大,而且非常容易出错,一般涉及到与线段的长度,或三角形的边有关的问题,尤其是这些线段若经过了原点[对应于极坐标系中的极点],此时采用极坐标系求解问题,有意想不到的便利。
分析:由\(2sin2A+sin(2B+C)=sinC\),
得到\(4sinAcosA+sin[(A+B+C)+B-A]=sinC\),即\(4sinAcosA+sin[\pi+B-A]=sinC\),
即\(4sinAcosA-sin(B-A)=sin(B+A)\),即\(4sinAcosA=sin(B-A)+sin(B+A)\),
则\(4sinAcosA=2sinBcosA\),即\(cosA(2sinA-sinB)=0\),
①当\(cosA=0\)时,\(A=\cfrac{\pi}{2}\),由\(C=\cfrac{\pi}{3}\),得到\(B=\cfrac{\pi}{6}\);
此时,\(b=\cfrac{2\sqrt{3}}{3}\),\(S_{\Delta ABC}=\cfrac{1}{2}bcsinA=\cfrac{1}{2}\cdot 2\cdot \cfrac{2\sqrt{3}}{3}=\cfrac{2\sqrt{3}}{3}\);
②当\(cosA\neq 0\)时,则有\(sinB=2sinA\),即\(b=2a\),
由\(\left\{\begin{array}{l}{a^2+b^2-ab=4}\\{b=2a}\end{array}\right.\),解得\(b=\cfrac{4\sqrt{3}}{3}\),\(b=\cfrac{2\sqrt{3}}{3}\),
故\(S_{\Delta ABC}=\cfrac{1}{2}absinC=\cfrac{1}{2}\cdot \cfrac{4\sqrt{3}}{3}\cdot \cfrac{2\sqrt{3}}{3}\cdot\cfrac{1}{2}=\cfrac{2\sqrt{3}}{3}\);
综上所述,\(S_{\Delta ABC}=\cfrac{2\sqrt{3}}{3}\);
Ⅱ、求\(\Delta ABC\)周长的最大值。
分析:具体解法见求三角形的周长类的取值范围
难点题目
【法1】: 由于 \(a=6\),设 \(b=x\),则\(c=2x\),可得\(: p=\cfrac{1}{2}(a+b+c)=3+\cfrac{3 x}{2}\)
所以 \(S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{(3+\cfrac{3}{2}x)(\cfrac{3}{2}x-3)(3+\cfrac{1}{2}x)(3-\cfrac{1}{2}x)}\)
\(=\sqrt{[(\cfrac{3}{2}x)^2-3^2][3^2-(\cfrac{1}{2}x)^2]}=\sqrt{(\cfrac{9x^2}{4}-9)(9-\cfrac{x^2}{4})}\)
\(=\sqrt{\cfrac{81x^2}{4}-\cfrac{9x^4}{16}-81+\cfrac{9x^2}{4}}=\sqrt{-\cfrac{9}{16}x^4+\cfrac{90}{4}x^2-81}\)
\(=\sqrt{-\cfrac{9}{16}(x^4-40x^2)-81}=\sqrt{-\cfrac{9}{16}(x^4-40x^2+20^2)-81+\cfrac{9}{16}\times 20^2}\)
\(=\sqrt{225-81-\cfrac{9}{16}(x^4-40x^2+20^2)}\)\(=\sqrt{144-\cfrac{9}{16}(x^{2}-20)^{2}}\)
由三角形的三边关系可知:\(\left\{\begin{array}{l}{x+2x>6}\\{x+6>2x}\\{6+2x>x}\end{array}\right.\),解得:\(2<x<6\)
故当\(x^2=20\),即当\(x=2\sqrt{5}\in (2,6)\)时, \(S_{\triangle ABC}\)取得最大值\(12\) 。 [1]
此时由\(\cfrac{1}{2}\times 2\sqrt{5}\times4\sqrt{5}\sin A=12\),解得:\(\sin A=\cfrac{3}{5}\)
解后反思:①明确海伦公式的作用,已知三边可以求解三角形的面积,或表示了三边,可以表达三角形的面积函数,从而可以求面积的最值;
②注意此题目的运算,有相当的难度,求最值时还涉及到复合函数;
③注意利用三角形的三边关系,求自变量的取值范围的技巧;
【法2】:由于\(|BC|=6\)为定值,求 \(\triangle ABC\)面积的最大值,只需要求出顶点 \(A\) 到 \(BC\) 边距离的最大值即可,注意到 \(AB=2AC\),从运动变化的视角,点 \(A\) 是运动变化的,因此有必要探索此点 \(A\) 的几何特征,即轨迹是什么。
如图,以 \(BC\) 所在的直线为 \(x\) 轴,以 \(BC\) 的中垂线为 \(y\) 轴建立直角坐标系 \(xOy\),易知点 \(B(-3,0)\), \(C(-3,0)\),
设点 \(A(x,y)\),则由 \(AB=2AC\)可得,\(\sqrt{(x+3)^2+y^2}=2\sqrt{(x-3)^2+y^2}\),
化简整理,得到 \((x-5)^2+y^2=16=4^2\),其中 \(x\neq0\),所以点 \(A\) 的轨迹是以点 \((5,0)\) 为圆心,以\(4\)为半径的圆(剔除 \(x\) 轴上的两个点),易知点 \(A\) 到 \(BC\) 边距离的最大值,即点 \(D\) 到 \(x\) 轴的距离,也即是圆的半径 \(4\) ,
故 \(\triangle ABC\) 的面积的最大值为 \(S_{\max}=\cfrac{1}{2}\times 6\times 4=12\),
此时点 \(A\) 位于 点 \(D\) 处,可知 \(AE=4\), \(BE=8\), 由勾股定理可知,\(AB=4\sqrt{5}\),同时 \(AE=4\), \(CE=2\),由勾股定理可知,\(AC=2\sqrt{5}\),
在 \(\triangle ABC\) 中,\(AB=4\sqrt{5}\),\(AC=2\sqrt{5}\),\(BC=6\),
由余弦定理可以求得,\(\cos A=\cfrac{(4\sqrt{5})^2+(2\sqrt{5})^2-6^2}{2\times4\sqrt{5}\times2\sqrt{5}}=\cfrac{4}{5}\),故 \(\sin A=\cfrac{3}{5}\) .
分析:根据题意设点\(A(x_1,y_1)\),\(B(x_2,y_2)\),\(P(x_0,y_0)\),
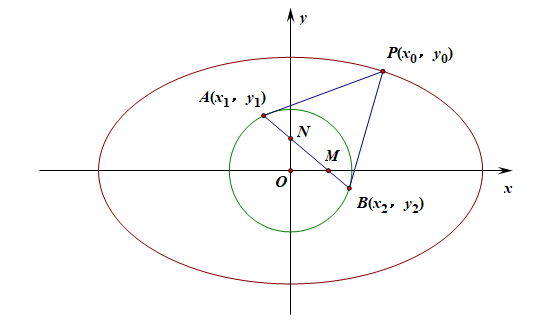
由于\(PA\)是圆的切线且切点为\(A\),则\(PA\)的方程为\(x_{1}x+y_{1}y=1\),[2]
同理\(PB\)的方程为\(x_{2}x+y_{2}y=1\),
由于点\(P(x_0,y_0)\)在切线\(PA\)上,则有\(x_{1}\cdot x_{0}+y_{1}\cdot y_{0}=1\);
点\(P(x_0,y_0)\)在切线\(PB\)上,同理则有\(x_{2}\cdot x_{0}+y_{2}\cdot y_{0}=1\)
又由于直线\(AB\)同时与直线\(PA\)和\(PB\)相交,
则由相同结构的两个表达式\(\left\{\begin{array}{l}{x_{1}\cdot x_{0}+y_{1}\cdot y_{0}=1}\\{x_{2}\cdot x_{0}+y_{2}\cdot y_{0}=1}\end{array}\right.\),
可以得到直线\(AB\)的方程为\(x_{0}x+y_{0}y=1\),[3]
则\(M\)的坐标为\((\cfrac{1}{x_{0}}, 0)\),\(N\)的坐标为\((0, \cfrac{1}{y_{0}})\),[4]
\(S_{\triangle OMN}=\cfrac{1}{2}|OM|\cdot|ON|=\cfrac{1}{2}\cdot\left|\cfrac{1}{x_{0} y_{0}}\right|\)
又由点\(P\)是椭圆\(M:\cfrac{x^{2}}{16}+\cfrac{y^{2}}{4}=1\)的动点,则有\(\cfrac{x_{0}^{2}}{16}+\cfrac{y_{0}^{2}}{4}=1\)
则有\(1=\cfrac{x_{0}^{2}}{16}+\cfrac{y_{0}^{2}}{4}\geqslant 2\sqrt{\cfrac{x_{0}^{2} y_{0}^{2}}{64}}=\cfrac{1}{4}\left|x_{0} y_{0}\right|\),
即\(\left|x_{0} y_{0}\right|\leqslant 4\)
\(S_{\triangle OMN}=\cfrac{1}{2}|OM||ON|=\cfrac{1}{2}\cdot\left|\cfrac{1}{x_{0} y_{0}}\right|\geqslant\cfrac{1}{8}\)
即\(\triangle OMN\)面积的最小值为\(\cfrac{1}{8}\).
解后反思:本题目的综合程度比较高,对学生的数学素养要求也比较高。
①过圆上任意一点的切线方程的求法;②合二为一的数学策略;③直线的截距式方程;④均值不等式在椭圆中的应用,⑤不等式性质;
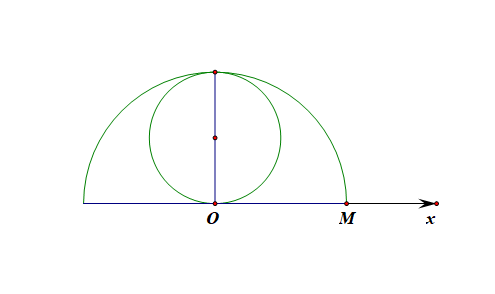
(1) 分别写出曲线 \(C_{1} 、 C_{2}\) 的极坐标方程;
解: 由题意可知, 曲线 \(C_{1}\) 是以极点 \(O\) 为圆心, 以 \(2\) 为半径的半圆,
结合图形可知, 曲线 \(C_{1}\) 的极坐标方程为 \(\rho=2\)(\(0\leq\theta\leq\pi\)).
设 \(P(\rho,\theta)\) 为曲线 \(C_{2}\) 上的任意一点, 可得 \(\rho=2\cos(\cfrac{\pi}{2}-\theta)=2\sin\theta\),
因此, 曲线 \(C_{2}\) 极坐标方程为\(\rho=2\sin\theta\)(\(0\leq\theta<\pi\)) .
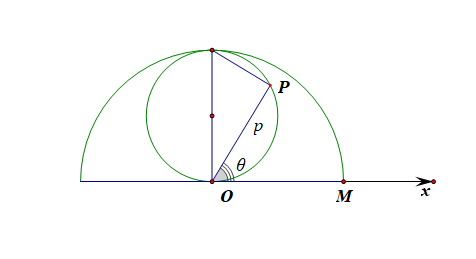
(2) 直线 \(\theta=\alpha\)(\(0<\alpha<\pi\),\(\rho\in R\)) 与曲线 \(C_{1}\) 、\(C_{2}\) 分别相交于点 \(A\) 、\(B\) (异于极点), 求 \(\triangle ABM\) 面积的最大值。
解法1:因为直线 \(\theta=\alpha\)(\(0<\alpha<\pi\), \(\rho\in R\)) 与曲线 \(C_{1}\) 、 \(C_{2}\) 分别相交于点 \(A\) 、 \(B\) (异于极点),
设 \(A(\rho_{_{A}},\alpha)\) 、\(B(\rho_{_{B}}, \alpha)\), 由题意得 \(\rho_{_{B}}=2\sin\alpha\), \(\rho_{A}=2\),
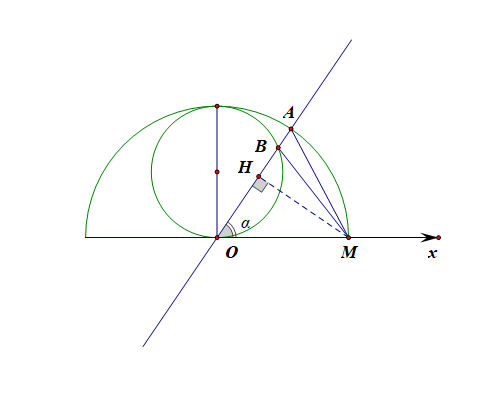
所以,\(|AB|=|\rho_{_{A}}-\rho_{_{B}}|=2-2\sin\alpha\),
因为点 \(M\) 到直线 \(AB\) 的距离为 \(d=|MH|=|OM|\sin\alpha=2\sin\alpha\),
所以, \(S_{\triangle ABM}\)\(=\)\(\cfrac{1}{2}|AB|\cdot d\)\(=\)\(\cfrac{1}{2}(2-2\sin\alpha)\cdot 2\sin\alpha\)
\(=\)\(2\sin\alpha(1-\sin\alpha)\)题目解答到此,既可以使用均值不等式求解最值,也可以考虑使用二次函数求最值;\(\leq 2 \times \cfrac{[(\sin\alpha+1)-\sin \alpha]^{2}}{4}=\cfrac{1}{2}\),
当且仅当 \(\sin\alpha=\cfrac{1}{2}\) 时, 等号成立, 故 \(\triangle ABM\) 面积的最大值为 \(\cfrac{1}{2}\) .
解法2:因为直线 \(\theta=\alpha\)(\(0<\alpha<\pi\), \(\rho\in R\)) 与曲线 \(C_{1}\) 、 \(C_{2}\) 分别相交于点 \(A\) 、 \(B\) (异于极点),
设 \(A(\rho_{_{A}},\alpha)\) 、\(B(\rho_{_{B}}, \alpha)\), 由题意得 \(\rho_{_{B}}=2\sin\alpha\), \(\rho_{A}=2\),
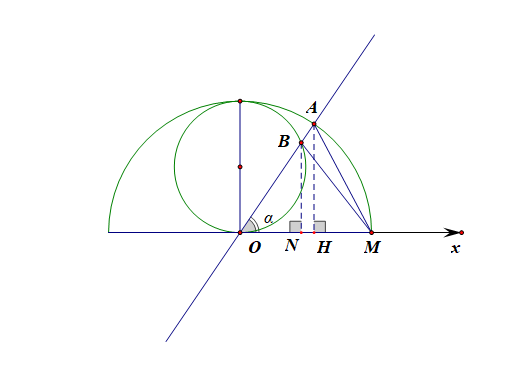
则 \(|AH|=2\times\sin\alpha\) ,\(|BN|=\rho_{_{B}}\times\sin\alpha=2\sin\alpha\times\sin\alpha=2\sin^2\alpha\),
\(S_{\triangle ABM}=S_{\triangle AOM}-S_{\triangle BOM}\)\(=\)\(\cfrac{1}{2}\times 2\times|AH|-\cfrac{1}{2}\times 2\times|BN|\)
\(=2\sin\alpha-2\sin^2\alpha\)\(=\)\(2\sin\alpha(1-\sin\alpha)\)题目解答到此,既可以使用均值不等式求解最值,也可以考虑使用二次函数求最值;\(\leq 2 \times \cfrac{[(\sin\alpha+1)-\sin \alpha]^{2}}{4}=\cfrac{1}{2}\),
当且仅当 \(\sin\alpha=\cfrac{1}{2}\) 时, 等号成立, 故 \(\triangle ABM\) 面积的最大值为 \(\cfrac{1}{2}\) .
设\(x^2=t\),则\(g(t)=144-\cfrac{9}{16}(t-20)^{2}\),是二次函数,图像开口向下,\(g(t)_{max}=g(20)=144\),
而函数\(m=\sqrt{n}\)是单调递增的,故\(\left[\sqrt{144-\cfrac{9}{16}(x^{2}-20)^{2}}\right]_{max}=\sqrt{144}=12\). ↩︎过圆\(x^2+y^2=r^2\)上的点\(P_0(x_0,y_0)\)的切线方程是\(x_0x+y_0y=r^2\);
证明:由于点\(P_0(x_0,y_0)\)在圆\(x^2+y^2=r^2\)上,故有\(x_0^2+y_0^2=r^2\),
又由于直线\(OP\)的斜率\(k_1=\cfrac{y_0}{x_0}\),故和直线\(OP\)垂直的圆的切线的斜率为\(k_0=-\cfrac{x_0}{y_0}\)
由点斜式可得,过圆上的点\(P_0(x_0,y_0)\)的切线方程为\(y-y_0=k_0(x-x_0)\),

即\(y-y_0=-\cfrac{x_0}{y_0}(x-x_0)\),整理为\(x_0x+y_0y=x_0^2+y_0^2\),又\(x_0^2+y_0^2=r^2\),
故整理得到切线方程为\(x_0x+y_0y=r^2\)。 ↩︎此处用到数学中的合二为一的策略,直线\(PA:x_{1}x_{0}+y_{1}y_{0}=1\),直线\(PB:x_{2}x_{0}+y_{2}y_{0}=1\),
故直线\(AB\)同时经过点\(A\)和点\(B\),由两点确定一条直线可知,此时只需要将同一结构的表达式中的\(x_1\),\(x_2\)换成\(x\),将\(y_1\),\(y_2\)换成\(y\),即得到直线\(AB\)的方程\(AB:x_{0}x+y_{0}y=1\)。 ↩︎将直线\(AB\)的方程为\(x_{0}x+y_{0}y=1\)变形为\(\cfrac{x}{\frac{1}{x_0}}+\cfrac{y}{\frac{1}{y_0}}=1\)[直线的截距式方程,由方程可以直接看出\(x\)截距和\(y\)截距],
故得到此直线和坐标轴的交点的坐标。\(M\left(\cfrac{1}{x_{0}}, 0\right)\),\(N\left(0, \cfrac{1}{y_{0}}\right)\). ↩︎

![求三角形面积的最值[范围]](https://images.cnblogs.com/cnblogs_com/wanghai0666/1784871/o_20080723074219735190_85.jpg) 高考中对三角形的面积的考查形式非常灵活,可以在三角函数题目中考查,也可以放到坐标系与参数方程中,更可以放置到圆锥曲线中,使用的求三角形面积公式也不一而足,故做一整理。
高考中对三角形的面积的考查形式非常灵活,可以在三角函数题目中考查,也可以放到坐标系与参数方程中,更可以放置到圆锥曲线中,使用的求三角形面积公式也不一而足,故做一整理。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号