图像处理基础(6)：锐化空间滤波器

前面介绍的几种滤波器都属于平滑滤波器（低通滤波器），用来平滑图像和抑制噪声的；而锐化空间滤波器恰恰相反，主要用来增强图像的突变信息，图像的细节和边缘信息。平滑滤波器主要是使用邻域的均值（或者中值）来代替模板中心的像素，消弱和邻域间的差别，以达到平滑图像和抑制噪声的目的；相反，锐化滤波器则使用邻域的微分作为算子，增大邻域间像素的差值，使图像的突变部分变的更加明显。

本位主要介绍了一下几点内容：

• 图像的一阶微分和二阶微分的性质
• 几种常见的一阶微分算子
• 二阶微分算子 - Laplace 拉普拉斯算子
• 一阶微分算子和二阶微分算子得到边缘的对比

一阶微分和二阶微分的性质

既然是基于一阶微分和二阶微分的锐化空间滤波器，那么首先就要了解下一阶和二阶微分的性质。

图像的锐化也就是增强图像的突变部分，那么我们也就对图像的恒定区域中，突变的开始点与结束点（台阶和斜坡突变）及沿着灰度斜坡处的微分的性质。微分是对函数局部变化率的一种表示，那么对于一阶微分有以下几个性质：

• 在恒定的灰度区域，图像的微分值为0.（灰度值没有发生变换，自然微分为0）
• 在灰度台阶或斜坡起点处微分值不为0.（台阶是，灰度值的突变变化较大；斜坡则是灰度值变化较缓慢；灰度值发生了变化，微分值不为0）
• 沿着斜坡的微分值不为0.

二阶微分，是一阶微分的导数，和一阶微分相对应，也有以下几点性质:

• 在恒定区域二阶微分值为0
• 在灰度台阶或斜坡的起点处微分值不为0
• 沿着斜坡的微分值为0.

从以上图像灰度的一阶和二阶微分的性质可以看出，在灰度值变化的地方，一阶微分和二阶微分的值都不为0；在灰度恒定的地方，微分值都为0.也就是说，不论是使用一阶微分还是二阶微分都可以得到图像灰度的变化值。

图像可以看着是二维离散函数，对于图像的一阶微分其计算公式如下：
在x方向，\(\frac{\partial f} {\partial x} = f(x + 1) - f(x)\).
在y方向，\(\frac{\partial f} {\partial y} = f(y + 1) - f(y)\)

对于二阶微分有:
在x方向，\(\frac{\partial^2 f} {\partial x^2} = f(x + 1) + f(x - 1) - 2 f(x)\).
在y方向，\(\frac{\partial^2 f} {\partial y^2} = f(y + 1) + f(y - 1) -2 f(y)\)

对于 图像边缘处的灰度值来说，通常有两种突变形式：

• 边缘两边图像灰度差异较大，这就形成了灰度台阶。在台阶处，一阶微分和二阶微分的值都不为0.
• 边缘两边图像灰度变化不如台阶那么剧烈，会形成一个缓慢变换的灰度斜坡。在斜坡的起点和终点一阶微分和二阶微分的值都不为0，但是沿着斜坡一阶微分的值不为0，而二阶微分的值为0.

对于图像的边缘来说，通常会形成一个斜坡过度。一阶微分在斜坡处的值不为0，那么用其得到的边缘较粗；而二阶微分在斜坡处的值为0，但在斜坡两端值不为0，且值得符号不一样，这样二阶微分得到的是一个由0分开的一个像素宽的双边缘。也就说，二阶微分在增强图像细节方面比一阶微分好得多，并且在计算上也要比一阶微分方便。

梯度图

在图像处理中的一阶微分通常使用梯度的幅值来实现。对于图像\(f(x,y)\),\(f\)在坐标\((x,y)\)处的梯度是一个列向量

\[\nabla f = grad(f) = \left[ \begin{array}{c} g_x \\ g_y \end{array} \right] = \left[\begin{array}{c} \frac{\partial f} {\partial x} \\ \frac{\partial f} {\partial y} \end{array} \right] \]

该向量表示图像中的像素在点\((x,y)\)处灰度值的最大变化率的方向。
向量\(\nabla f\)的幅值就是图像\(f(x,y)\)的梯度图，记为\(M(x,y)\)

\[M(x,y) = mag(\nabla f) = \sqrt{g_x^2 + g_y^2} \]

\(M(x,y)\)是和原图像\(f(x,y)\)同大小的图像。由于求平方的根运算比较费时，通常可以使用绝对值的和来近似

\[M(x,y) \approx \mid g_x \mid + \mid g_y \mid \]

从上面可以看出，要得到图像的梯度图，有以下步骤：

• 图像在x方向的梯度\(g_x\)
• 图像在y方向的梯度\(g_y\)
• \(M(x,y) = \mid g_x \mid + \mid g_y \mid\)

一阶梯度算子

图像是以离散的形式存储，通常使用差分来计算图像的微分，常见的计算梯度的模板有以下几种

• 根据梯度的定义

\[g_x = f(x+1,y) - f(x,y) \\ g_y = f(x,y+1) - f(x,y) \]

可以得到模板\(\left[ \begin{array}{c} -1 & 1\end{array}\right]\) 和 \(\left[ \begin{array}{c} -1 \\ 1\end{array}\right]\)。
使用该方法计算的图像的梯度只是考虑单个像素的差值，并没有利用到图像的像素的邻域特性。

• Robert交叉算子
  在图像处理的过程中，不会只单独的对图像中的某一个像素进行运算，通常会考虑到每个像素的某个邻域的灰度变化。因此，通常不会简单的利用梯度的定义进行梯度的计算，而是在像素的某个邻域内设置梯度算子。考虑，$3 \times 3 $区域的像素，使用如下矩阵表示：

\[\left[ \begin{array}{ccc} z_1 & z_2 & z_3 \\ z_4 & z_5 & z_6\\z_7 & z_8 & z_9 \end{array} \right] \]

令中心点\(z_5\)表示图像中任一像素，那么根据梯度的定义，\(z_5\)在在x和y方向的梯度分别为：\(g_x = z_9 - z_5\)和\(g_y = z_8 - z_6\)，梯度图像M(x,y)$$M(x,y) \approx \mid z_9 - z_5 \mid + \mid z_8 - z_6 \mid$$
根据上述公式，Robert在1965年提出的Robert交叉算子

\[\left[ \begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array} \right] and \left[ \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right] \]

• Sobel算子
  Robert交叉算子的尺寸是偶数，偶数尺寸滤波器没有对称中心计算效率较低，所以通常滤波器的模板尺寸是奇数。仍以\(3 \times 3\)为例，以\(z_5\)为对称中心（表示图像中的任一像素），有

\[g_x = (z_7 + 2z_8 +z_9) - (z_1 + 2z_2 + z_3) \\ g_y = (z_3 + 2z_6 + z_9)-(z_1 + 2z_4 + z_7) \]

利用上述公式可以得到如下两个卷积模板，分别计算图像在x和y风向的梯度

\[\left[ \begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{array} \right] 和 \left[ \begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array} \right] \]

第一个模板，第三行和第一行的差近似x方向的偏微分；第二个模板，第三列和第一列的差近似y方向的偏微分，而且模板的所有系数只和为0，表示恒定灰度区域的响应为0.

基于OpenCV的一阶梯度算子实现

• Sobel算子
  在OpenCV中封装了Sobel算子，其函数为Sobel。使用Sobel能够很方便的计算任意尺寸的x和y方向的偏微分，具体如下：

void sobel_grad(const Mat &src, Mat &dst)
{
    Mat grad_x, grad_y;

    Sobel(src, grad_x, CV_32F, 1, 0);
    Sobel(src, grad_y, CV_32F, 0, 1);
    
    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 0.5, grad_y, 0.5, 0, dst);

    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}

上述代码中调用Sobel分别得到图像在x和y方向的偏微分\(g_x\)和\(g_y\)，然后相加得到得到图像的梯度图。
其余的几个函数说明,convertScaleAbs将图像类型转换为CV_8U；addWeighted按一定的权值将两个图像相加；magnitude求两个图像的幅值，其公式为\(dst=\sqrt{g_x^2 + g_y^2}\)，具体的参数说明可参考OpenCV的官方文档。

• 基于定义和Robert交叉算子的计算
  对于这两种算子，OpenCV中并没有提供具体的函数，不过可以利用filter2D函数来实现。filter2D是OpenCV中对图像进行卷积运算的一个很重要的函数，该函数能够使用任意的线性卷积核对图像进行卷积运算。

void robert_grad(const Mat& src, Mat &dst)
{
    Mat grad_x, grad_y;

    Mat kernel_x = (Mat_<float>(2, 2) << -1, 0,0,1);
    Mat kernel_y = (Mat_<float>(2, 2) << 0, -1, 1, 0);
    
    filter2D(src, grad_x, CV_32F, kernel_x);
    filter2D(src, grad_y, CV_32F, kernel_y);

    //convertScaleAbs(grad_x, grad_x);
    //convertScaleAbs(grad_y, grad_y);
    //addWeighted(grad_x, 1, grad_y, 1, 0, dst);
    magnitude(grad_x, grad_y, dst);
    convertScaleAbs(dst, dst);
}

构造好Robert交叉算子，然后调用filter2D即可；基于定义的计算方法于此类似，不在赘述。

结果三种方法计算得到的梯度图，如下：

从上面结果可以看出，Robert交叉算子和基于定义得到的边缘图，得到的边缘较细并且不是很连续；Sobel得到边缘较粗，线条连续，效果明显好于其他的两种算子。

二阶微分算子 - LapLace 拉普拉斯算子

二阶微分算子的代表就是拉普拉斯算子，其定义如下：

\[\nabla ^2 f = \frac{\partial^2 f} {\partial x^2} + \frac{\partial^2 f} {\partial y^2} \]

其中：

\[\frac{\partial^2 f} {\partial x^2} = f(x + 1,y) + f(x - 1,y) - 2 f(x,y) \\ \frac{\partial^2 f} {\partial y^2} = f(x,y + 1) + f(x,y - 1) -2 f(x,y) \]

对于上述的$3 \times 3 $区域，则有

\[\nabla ^2 f = z_2 + z_4 + z_6 + z_8 - 4z_5 \]

其得到的模板如下：

\[\left[ \begin{array}{ccc} 0 & 1 & 0 \\ 1 &-4 & 1 \\ 0 & 1 & 0 \end{array} \right] 或 \left[ \begin{array}{ccc} 0 & -1 & 0 \\ -1 &4 & -1 \\ 0 & -1 & 0 \end{array} \right] \]

注意，模板中心的符号，并且模板的所有系数之和为0.

在OpenCV中有对LapLace的封装，其函数为Laplacian,其使用的模板中心的系数为负，具体参数说明参见OpenCV文档，其得到的边缘图和一阶微分算子得到边缘图对比结果如下：

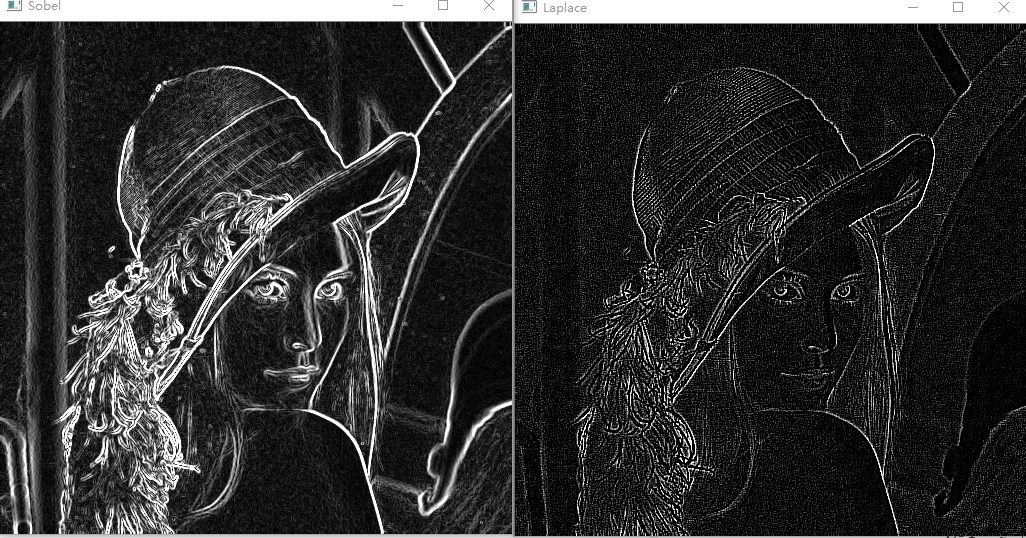
• 一阶微分算子Sobel得到的边缘较粗
• 二阶微分算子Laplace得到的边缘则较细，并且边缘是双边缘
• Lpalace算子对噪声比较敏感，得到的边缘图像上噪声较明显

由于Laplace算子对噪声敏感，会得到双边，并且并不能检测边缘的方向，其通常不用于直接的边缘检测，只是起到辅助作用。检测某像素实在边缘的亮的一侧还是暗的一侧，利用“零跨越”确定边缘的位置。

总结

本文主要介绍了图像空间域的锐化算子（也就是边缘检测算子），这些算子都是基于图像的微分的：一阶微分和二阶微分（拉普拉斯算子）。
由于一阶微分和二阶微分有各自的特点，其得到的图像边缘也不相同：一阶微分得到的图像边缘较粗，二阶微分得到的是较细的双边缘，所以在图像的边缘增强方面二阶微分算子的效果较好。

唠叨几句，看了下上一篇博客还是2月下旬发的，而今已是6月了，蹉跎了近4个月的时间！感觉工作上实在学不到什么东西啊，每日忙来忙去没有什么收获，而且本身也不是自己喜欢做的方向，是不是该考虑换个工作了呢。