题解：P9339 [JOISC 2023] Cookies (Day3)

题意

有 \(K\) 种颜色的球，第 \(i\) 种颜色的球有 \(A_i\) 个。另外给定一个集合 \(B\)，里面有 \(M\) 个数 \(B_1,B_2,\cdots,B_M\)。

现在要把球堆成若干堆，要求：

• 每堆不能有重复颜色；
• 每堆的大小是 \(B_1,B_2,\cdots,B_M\) 中的一个数。

请你最小化堆数，并输出方案。

题解

设最终有 \(n\) 堆，高度为 \(H_1,H_2,\cdots,H_n\)。交换堆的顺序肯定是没有影响的，为了方便，对于下文（包括后文移动完之后），我们不妨设 \(H\) 不增。

考虑如何判定这样一个序列合法。这也是我们得出答案序列后，求颜色方案的方法。

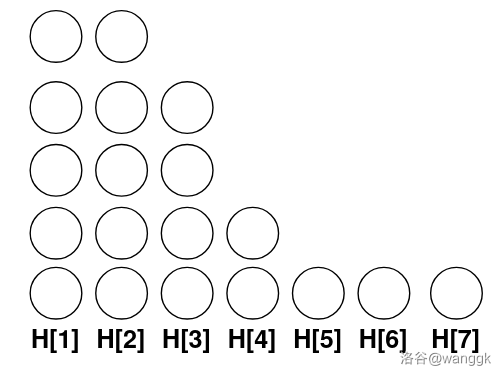
我们要求每一堆没有相同颜色，那么按照出现次数从大到小加入颜色。

对于每种颜色，从左往右，将离目标高度 \(H_i\) 最远的堆叠高一层。因为是优先叠那些最拖后腿的堆，这样的贪心是最优的。如果高度序列可能被达到，那么该最终状态合法。

因为我们是贪心地向上叠（先消耗出现次数多的颜色，先消耗比较高的堆，最可能合法），所以我们发现，对于一个合法局面，把前面堆的元素移到后面，也一定是合法的，如下图。

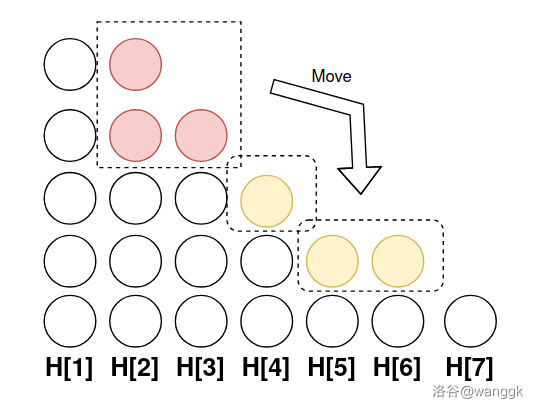
这是很好理解的，因为“拖后腿”的堆变矮了，颜色不重复的限制就变松了。

于是我们只需要限制最紧（找到前面的堆最多）的合法状态，再统计不超过这个的局面数量，就可以了。这个非常简单，只需要所有颜色都放一个前缀：

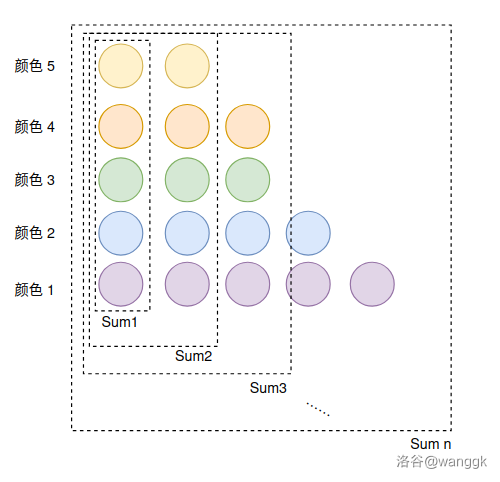
我们得到了尽可能最靠前放的序列，记其前缀和为 \(Sum\)（如图），合法序列 \(H_n\) 一定满足：

• 单调不增排序后，\(\forall i \in [1,n],\sum_{j \leq i} \leq Sum_i\)

最小堆数看起来不是很好转移，那就设计一个可行性 DP：设 \(f_{i,j,k}\) 表示，考虑完了前 \(i\) 大的高度，用了 \(j\) 堆，目前前缀和为 \(k\)，是否可行。转移有两种，继承前一层 \(i-1\) 的值，和在本层中拿一个（相当于完全背包）：

\[f_{i,j,k} \leftarrow f_{i-1,j,k} \or f_{i,j-1,k-B_i} (k \leq Sum_j) \]

括号内表示转移条件，另外我们已经将 \(B\) 降序排序，即 \(B_1 > B_2> \cdots > B_n\)。

同时由于前缀和不超过 \(k\)，则 \(j \leq \frac{k}{B_i}\)，所以 \(j\) 是 \(\log\) 级别的，再用 bitset 优化可行性 DP（优化完全背包的部分），复杂度就降到了 \(O(\frac{n^2 \log n}{w})\)，就可以通过了。

代码

看起来挺可读的。

#include<bits/stdc++.h>
#define For(i,il,ir) for(int i=(il);i<=(ir);++i)
#define Rof(i,ir,il) for(int i=(ir);i>=(il);--i)
using namespace std;
typedef pair<int,int> pii;
const int maxn=15005;

int n,m,V;
int a[maxn],b[maxn],sum[maxn];

bitset<maxn> pw[maxn];
vector<bitset<maxn> > f[maxn];

void prework()
{
    scanf("%d",&n);
    For(i,1,n){
        scanf("%d",&a[i]); V+=a[i];
        For(j,1,a[i]) sum[j]++;
    }
    pw[0].set(0);
    For(i,1,V){
        sum[i]+=sum[i-1];
        pw[i]=pw[i-1]<<1,pw[i].set(0);
    }
    scanf("%d",&m);
    For(i,1,m) scanf("%d",&b[i]);
    reverse(b+1,b+1+m);
}

int res[maxn];
vector<int> sol[maxn];
void dfs(int i,int j,int k){
    if(!i||!j||!k) return;
    if(k>=b[i] && f[i][j-1][k-b[i]]) res[j]=b[i],dfs(i,j-1,k-b[i]);
    else dfs(i-1,j,k);
}
signed main()
{
    prework();
    bitset<maxn> tmp; tmp.set(0);
    f[0].push_back(tmp),b[0]=V+1;
    For(i,1,m) For(j,0,V/b[i])
    {
        bitset<maxn> dp;
        if(j) dp|=(f[i][j-1]<<b[i]);
        if(b[i-1]*j<=V) dp|=f[i-1][j];
        dp&=pw[sum[j]];
        f[i].push_back(dp);
    }
    
    int ans=-1;
    For(j,0,V/b[m]) if(f[m][j][V]){ ans=j; break; }
    printf("%d\n",ans);
    if(ans==-1) return 0;
    else dfs(m,ans,V);

    priority_queue<pii> q,q2;
    For(i,1,n) q.push(make_pair(a[i],i));
    For(i,1,ans)
    {
        printf("%d ",res[i]);
        while(res[i]--){
            pii x=q.top(); q.pop();
            printf("%d ",x.second);
            if(--x.first); q2.push(x);
        }printf("\n");
        while(!q2.empty()) q.push(q2.top()),q2.pop();
    }
    return 0;
}