合并若干次后的状态是几个大集合，把每个集合堆成一堆，每个集合的大小就是这堆的高度 \(H_i\)。

不妨设 \(H\) 不增，否则并不是本质不同的状态。

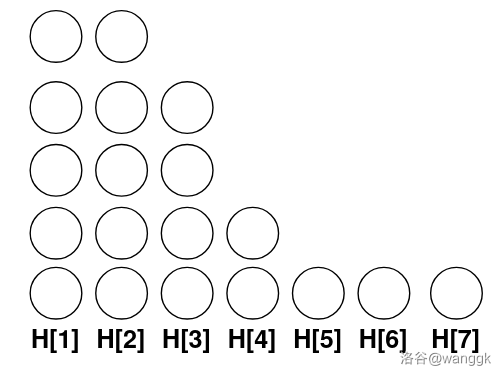
考虑如何检验上述状态是否合法，我们要求每一堆没有相同颜色，那么按照出现次数从大到小加入颜色，每次从左往右将能叠高的堆叠高一层。

如果高度序列可能被达到，那么该最终状态合法。

因为我们是贪心地向上叠（先消耗出现次数多的颜色，先消耗比较高的堆，最可能合法），所以我们发现，对于一个合法局面，把前面堆的元素移到后面，一定是合法的。

当然，移动完之后仍然需要保证序列 \(H\) 不增，否则会重复统计。

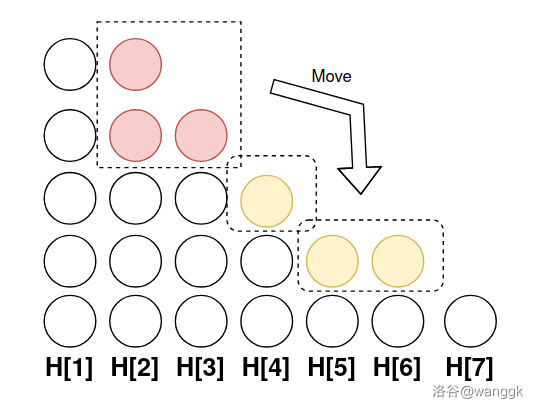
于是我们只需要找到前面的堆最多的状态，再统计不超过这个的局面数量就可以了。这个非常简单，只需要所有颜色都放一个前缀就可以了（最后面的堆可能为空）：

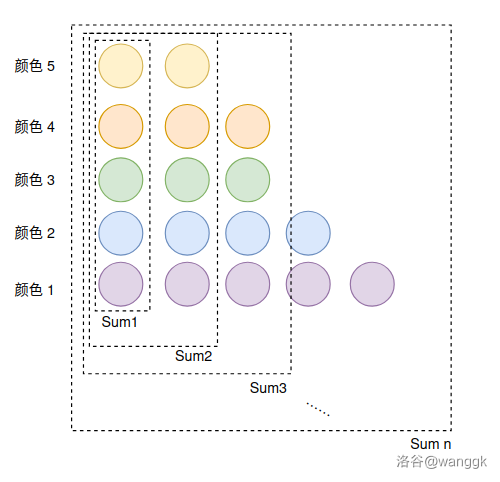
我们得到了尽可能最靠前放的序列，记其前缀和为 \(Sum\)（如图），合法序列 \(H_n\) 一定满足：

• 单调不增。
• \(\forall i \in [1,n],\sum_{j \leq i} \leq Sum_i\)

找完性质之后 DP 就不难了，设 \(f_{i,j,k}\) 表示到第 \(i\) 项，目前前缀和为 \(j\)，最小值大于等于 \(k\) 的方案数。

前一项表示这一位填的数大于 \(k\)，后一项表示这一位恰好填 \(k\)。

最后答案就是 \(f_{n,n,0}\)。

第一维可以滚动数组，另外由于 \(k \leq \frac{j}{i}\)，所以 \(k\) 是 \(\log\) 级别的，因此复杂度是对的。

CF 提交记录

#include<bits/stdc++.h>
#define For(i,il,ir) for(int i=(il);i<=(ir);++i)
#define Rof(i,ir,il) for(int i=(ir);i>=(il);--i)
using namespace std;
typedef long long ll;
const int maxn=2005;
const ll mod=998244353;
void qadd(ll &x,ll y){ x=(x+y>=mod)?(x+y-mod):(x+y); }

int n,x;
int c[maxn],h[maxn],s[maxn];
ll f[2][maxn][maxn];

signed main()
{
	scanf("%d",&n);
	For(i,1,n) scanf("%d",&x),c[x]++;
	For(i,1,n) For(j,1,c[i]) h[j]++;
	For(i,1,n) s[i]=s[i-1]+h[i];
	
	For(k,0,n) f[0][0][k]=1ll;
	For(i,1,n){
		int nw=i&1,lt=(i&1)^1;
		For(j,0,s[i])
			Rof(k,j/i,0){
				f[nw][j][k]=0;
				if(k+1<=j/i) qadd(f[nw][j][k],f[nw][j][k+1]);
				if(i==1 || k<=(j-k)/(i-1)) qadd(f[nw][j][k],f[lt][j-k][k]);
			}
	}
	printf("%lld\n",f[n&1][n][0]);
	return 0;
}