5.16打卡

一、问题描述：

本节要研究孪生素数的问题，先来看看什么是孪生素数。
所谓孪生素数指的是间隔为2的两个相邻素数，因为它们之间的距离已经近的不能再近了，如同李生兄弟一样，所以将这一对素数称为孪生素数。
显然，最小的一对孪生素数是(1，3)。我们可以写出3～100以内的孪生素数，一共有8对，分别是(3，5)，(5，7)，(11，13)，(17，19)(29，31)，(41，43)，(59，61)和(71，73)。随着数字的增大，孪生素数的分布也越来越稀疏，人工寻找孪生素数变得非常困难。
关于孪生素数还存在着一个著名的猜想——孪生素数猜想，即孪生素数是否有无穷多对，这是数论中还有待解决的一个重要问题。此处我们只讨论在有限范围内的孪生素数求解问题。
本节要解决的问题是：编程求出3~1000以内的所有孪生素数。

二、设计思路：
在问题分析中，我们已经确定要采用穷举法逐一考察3～1000以内的每个整数，因此在本题的算法设计中需要采用循环结构。
在判断是否为素数时可以定义一个函数prime)，每次判断整数n是否为素数时都将n作为实参传递给函数prime()，在prime()函数中使用前面介绍过的判别素数的方法进行判断。如果n为素数，则prime(函数返回值为1，否则prime()函数返回值为0。

三、程序流程图

 

 

 

 

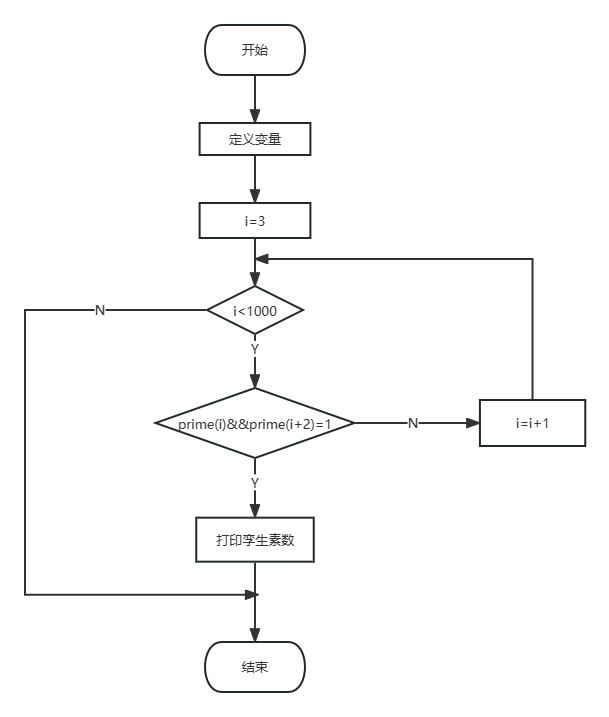
四、代码实现

#include<stdio.h>

#include<math.h>

int prime(int n)

{

    int j;

    long k;

    k=sqrt(n)+1;

    for(j=2;j<=k;j++)

    {

        if(n%j==0)

            return 0;

    }

    return 1;

}

int main()

{

    int i,count=0;

    printf("The twin prime pairs between 3 and 1000 are: \n");

    for (i=3;i<1000;i++)

        if(prime(i)&&prime(i+2))

    {

        printf("(%-3d,%3d) ",i,i+2);

        count++;

        if(count%5==0)

            printf("\n");

 

    }

}