机械臂逆运动学的数值方法及其MATLAB实现

机械臂逆运动学的数值方法

一 数值方法特点

1. 优势

• 计算简单：数值方法通常不需要进行复杂的矩阵运算或解析推导，因此计算过程相对简单直接。这使得在编程实现时，代码更加简洁易懂。
• 通用性强：数值方法对于不同类型的机械臂和不同的逆运动学问题都具有一定的适用性。通过调整算法参数和迭代策略，可以较好地适应各种复杂情况。
• 处理非线性：对于一些具有复杂非线性关系的机械臂系统，数值方法能够通过迭代优化等方式找到满足精度要求的解。这在一定程度上弥补了解析方法在处理复杂问题时的不足。
• 计算精度高：在迭代次数足够多的情况下，数值方法可以达到较高的计算精度，满足机械臂运动控制的需求。

2. 缺点

• 实时性差：数值方法通常需要进行大量的迭代计算，这会导致计算时间较长，从而影响机械臂的实时性。在实时性要求较高的场合，数值方法可能无法满足需求。
• 对初始值敏感：数值方法的求解结果往往受到初始值选择的影响。如果初始值选择不当，可能会导致算法收敛到局部最优解而非全局最优解，甚至导致算法发散。
• 计算量大：为了得到满足精度要求的解，数值方法往往需要进行多次迭代计算。这不仅增加了计算量，还可能影响机械臂的运动效率。
• 位形不可预测：在迭代过程中，机械臂的位形可能会发生变化，而这些变化往往是不可预测的。这可能会导致机械臂在运动过程中与障碍物发生碰撞或超出工作空间等安全问题。

二 数值方法逆解建模

设\(x \in R^m\)是笛卡尔坐标系下机械臂末端位姿最小表达，\(q \in R^n\)是机械臂的关节变量，其中\(m\)为空间自由度个数，\(n\)为机械臂的自由度个数。

n连杆机械臂的正运动学模型可表示为：

\[x=f(q) \]

其逆运动学模型可表示为：

\[q=f^{-1}(x) \]

其中\(f:R^n \rightarrow R^m\)

记

\[F(q) = \frac{1}{2}(f(q)-x^d)^T(f(q)-x^d) \]

则逆解问题可转化最小值的优化问题

\[\underset{q\in{R^n}}{min} F(q) = \underset{q\in{R^n}}{min} \frac{1}{2}(f(q)-x^d)^T(f(q)-x^d) \]

其中\(x^d\)为期望的末端位姿

三 数值方法逆解算法

1. 牛顿-拉夫逊法(Newton-Raphson)

为了寻找满足给定期望位姿\(x^d\)的关节角度\(q^d\)，在\(q^d\)处进行taylor展开正运动学模型\(f(q)\)，可得：

\[f(q)=f(q^d)+J(q^d)(q-q^d)+h.o.t. \]

忽略高阶项h.o.t.，进一步得到：

\[q-q^d=J^{-1}(q)(f(q)-f(q^d)) \]

如果Jacobian矩阵不为方阵或者不可逆,可使用\(J^+=J^T(JJ^T)^{-1}\)作为伪逆代替\(J^{-1}\)。通过迭代序列：

\[q_{k+1}=q_{k}-\alpha_kJ^{-1}(q_k)(f(q_k)-x^d),k=0,1,2,... \]

可得到收敛到所求位姿\(x^d\)的解\(q^d\)；其中\(\alpha_k>0\)为步长系数，可通过调节其以实现快速收敛，其可以选择为一个常数、一个标量或者对角阵，也可以根据随迭代次数k变化。

注意：该方法是基于运动学模型的一阶导数估计，只能局部收敛，此外，通常对一个位姿机械臂存在多解问题，此外，由于求逆操作的存在，该方法可能需处理矩阵奇异的情况

2. 梯度下降法(Gradient Descent)

针对 二 数值方法逆解建模 中转化的最小值问题，使用梯度下降算法作为优化方法来求\(F(q)\)的最小值。\(F(q)\)的梯度为：

\[\nabla{F(q)} = J^T(q)(f(q)-x^d) \]

梯度下降法的迭代序列为:

\[q_{k+1}=q_{k}-\alpha_k\nabla{F(q)} =q_{k}-\alpha_kJ^{T}(q_k)(f(q_k)-x^d),k=0,1,2,... \]

其中\(\alpha_k>0\)为步长系数，可通过调节其以实现快速收敛，其可以选择为一个常数、一个标量或者对角阵，也可以根据随迭代次数k变化。

相较于牛顿-拉夫逊法，该方法的优点是不需要计算Jacobian矩阵的逆(伪逆)，不用处理奇异性问题。但通常来说，该方法的收敛速度较慢

3. 高斯-牛顿法(Guass-Newton)

针对 二 数值方法逆解建模 中转化的最小值问题，使用高斯-牛顿法作为优化方法来求\(F(q)\)的最小值。

高斯-牛顿法的迭代序列为:

\[q_{k+1} =q_{k}-\alpha_k(J(q_k)^TJ(q_k))^{-1}J^{T}(q_k)(f(q_k)-x^d),k=0,1,2,... \]

可以发现：若在 1. 牛顿-拉夫逊法(Newton-Raphson) 中使用\(J^+=J^T(JJ^T)^{-1}\)作为伪逆代替\(J^{-1}\)，此时高斯-牛顿法(Guass-Newton)等价于牛顿-拉夫逊法(Newton-Raphson)

其中\(\alpha_k>0\)为步长系数，可通过调节其以实现快速收敛，其可以选择为一个常数、一个标量或者对角阵，也可以根据随迭代次数k变化。

该方法在某些情况下等价于牛顿-拉夫逊法(Newton-Raphson)，需要注意的是其还需要处理\(J(q_k)^TJ(q_k)\)不可逆的情况！

4. 列文伯格-马夸尔特法(Levenberg–Marquardt)

针对 二 数值方法逆解建模 中转化的最小值问题，使用列文伯格-马夸尔特法作为优化方法来求\(F(q)\)的最小值。

列文伯格-马夸尔特法的迭代序列为:

\[q_{k+1} =q_{k}-\alpha_k(J(q_k)^TJ(q_k)+\mu I)^{-1}J^{T}(q_k)(f(q_k)-x^d),k=0,1,2,... \]

其中\(\alpha_k>0\)为步长系数，可通过调节其以实现快速收敛，其可以选择为一个常数、一个标量或者对角阵，也可以根据随迭代次数k变化。\(\mu>0\)为阻尼系数可通过调节其以实现快速收敛，其同样也可以选择为一个常数、一个标量或者对角阵，也可以根据随迭代次数k变化。

可以发现：

当\(\mu\)很大时，这时\((J(q_k)^TJ(q_k)+\mu I)^{-1} \approx \mu^{-1}I\)算法近似为梯度下降法。

当\(\mu\)较小时，这时\((J(q_k)^TJ(q_k)+\mu I)^{-1} \approx (J(q_k)^TJ(q_k))^{-1}\)算法高斯-牛顿法。

通过这个特性，在初期可以将\(\mu\)设置较大，快速收敛到解的区域，在后期将\(\mu\)设置较小，进一步快速收敛到满足精度要求的解附近。

该方法结合结合了梯度下降和高斯-牛顿法的特点，通过引入了阻尼因子，不需要处理不可逆的情况，可以快速稳定的收敛到解的位置！

四 各种算法比较

在MATLAB中建立20自由度机械臂正运动学模型，使用余弦变化的步长因子加快算法收敛，使用MATLAB优化工具箱，对步长最大值和最小值参数进行寻优优化。完成参数优化后。随机生成16000组关节变量，分别采用牛顿-拉夫逊法、列文伯格-马夸尔特法求解逆运动学(梯度下降法法收敛过慢不考虑)，设置求解精度为1e-8,最大迭代数为500，16000组求逆解数据的迭代次数总计、平均值、中位数如下表：

	总计	平均值	中位数
L-M算法	994086	29	62.1304
N-R算法	1820544	61	113.7840

随机抽取8组求解逆解迭代次数如下：

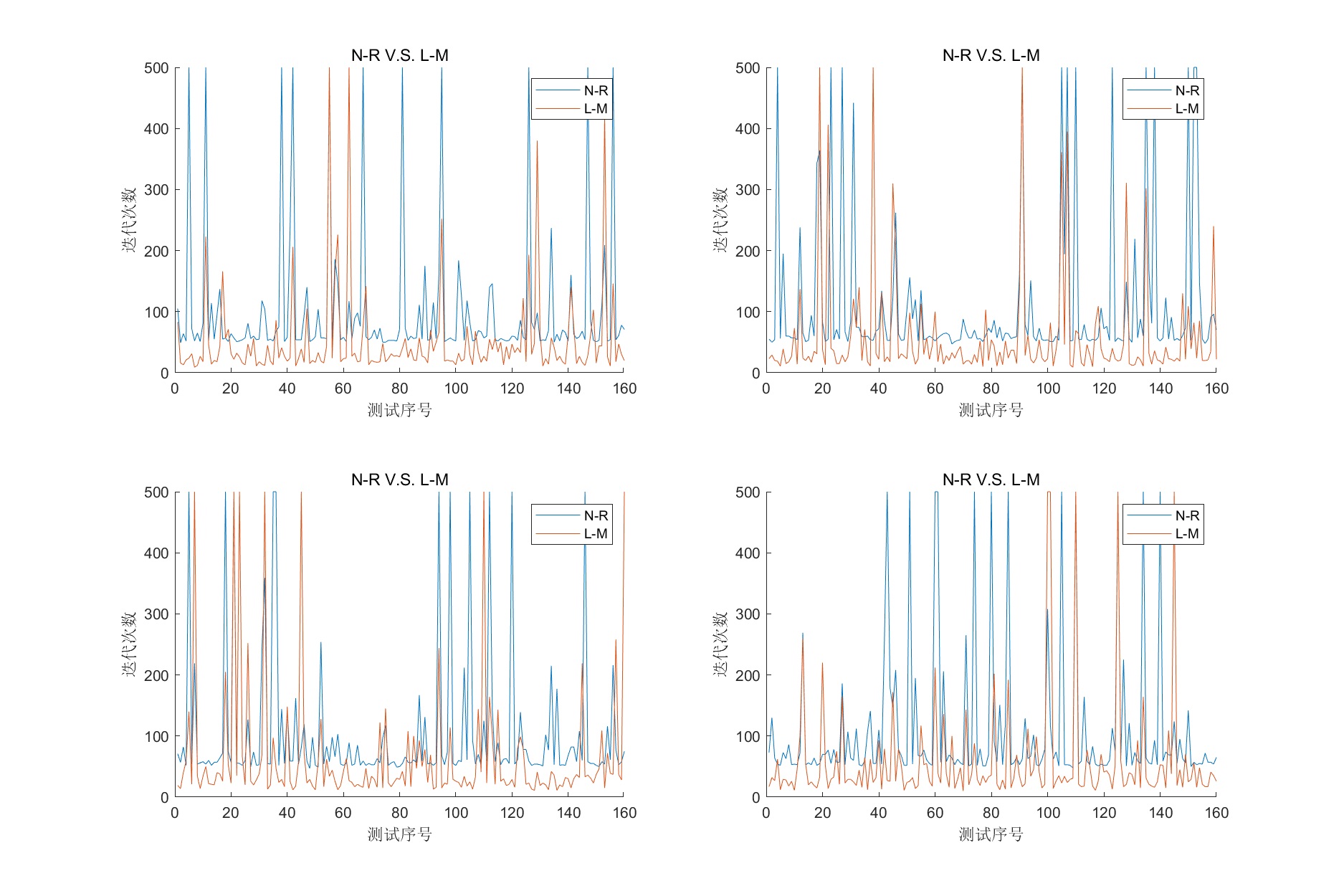
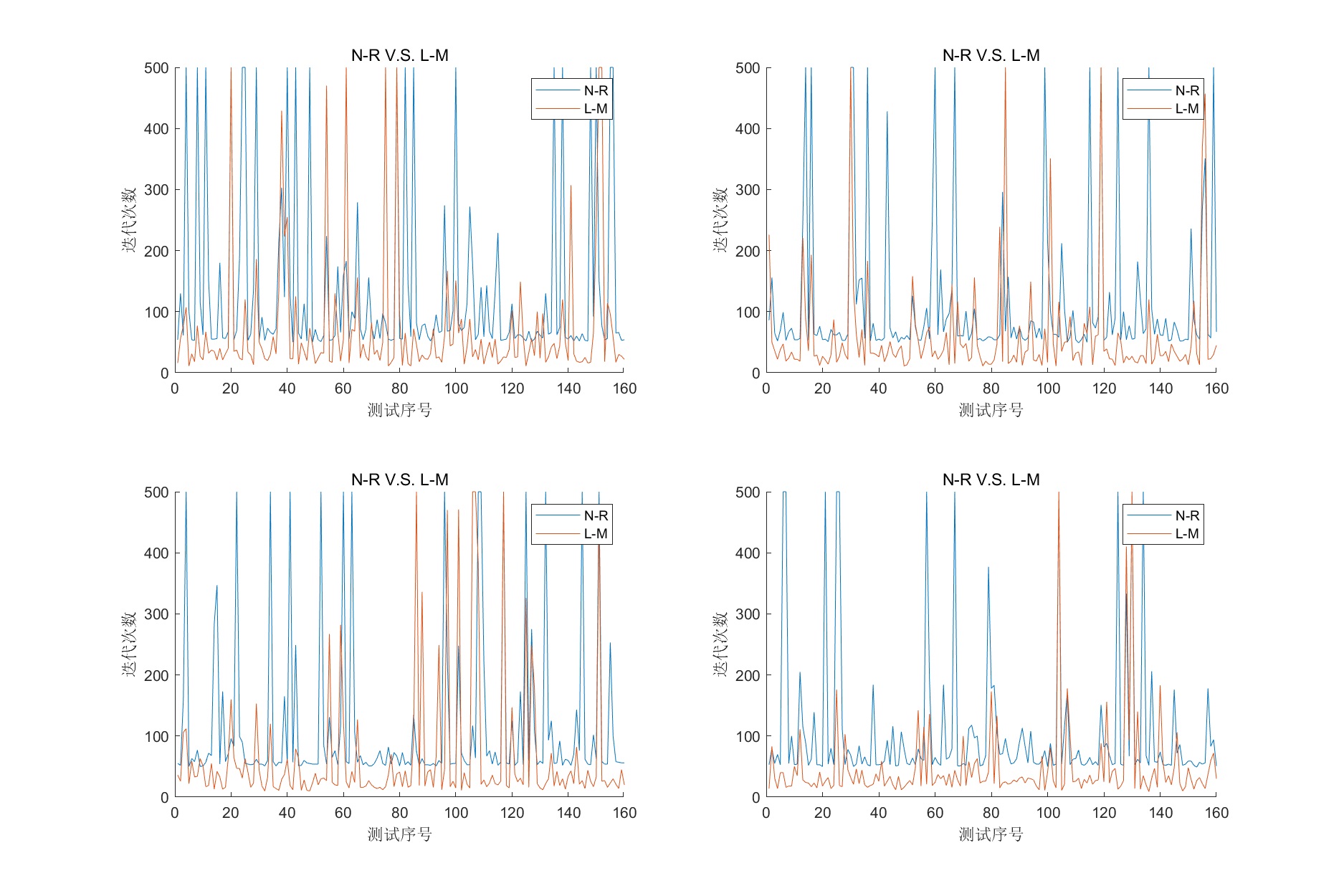
可以明显的看出列文伯格-马夸尔特法收敛速度快于牛顿-拉夫逊法

最后贴出本文所使用的代码：代码链接

欢迎大家一起交流！！！