面向对象第一单元总结

面向对象第一单元总结

  第一单元的内容为表达式解析计算，主要训练了对层次化结构的理解，和面向对象思维的基本运用。

---

三次作业的设计与迭代

第一次作业

  最初看到第一次作业有些不知所措：表达式计算曾在数据结构中实现过，因此第一反应纯纯是面向过程，用数据结构和算法直接实现。但毕竟是面向对象课程，每一个任务都是为了更好地掌握面向对象思维与设计。看着一串串表达式，一个个整体浮现于我脑海，却怎么也拆分不成一个个分层次的对象。直到做完了指导书的训练，我才恍然大悟，原来可以以符号的连接方式来分层：单一元素构成变量，乘号连接的整体是一个项，由很多因子组成，而最高层次的表达式由加减号连接的各个项组成。同时，表达式也可以成为因子居于项中，形成递归。

  大体层次分好，接下来是分工问题。数据部分，我以指导书代码为原型，抽象出Factor接口，由表达式和变量类实现。如今想来，这种抽象是行为层次的抽象，表达式和变量都具有乘法、自反等行为特征，抽象出接口后便于统一管理，为项的功能实现做好了铺垫。功能部分我直接套用指导书方法，用专门的类去识别字符串，另一个类解析出数据对象。这样的设计分工明确，便于实现。

  在具体实现过程中还有几个优化。第一次只有x变量，因此每一项可以化简成a*x**b次方的形式，即可以以x的次方唯一标识一个表达式中的一项。进而以指数为key，变量对象为value便可设计出一个HashMap，便于统一管理同时便于输出。其次关于表达式的计算化简：化简也是递归形式，表达式调用每个项的化简方法，如果项里的因子是表达式则会再调用表达式的化简方法，直到递归到最底层(变量)便可开始往上返回。计算的难点在于实现乘法。抽象出乘法方法后便可在Term类中直接统一调用方法每项相乘，得出最终的对象，再以Factor的形式返回，同样是便于统一管理。

  第一次的作业完成得还是比较迷茫，因为大多数思路照搬于指导书，很多精妙之处在后面的开发中才逐渐想通。这次简单功能的实现算是面向对象思想的初步建立，了解了怎样将终极目标按照层次逐步缩小，分离出能很轻易实现的对象，对象也有自己的属性和方法，能完成自己的职责。

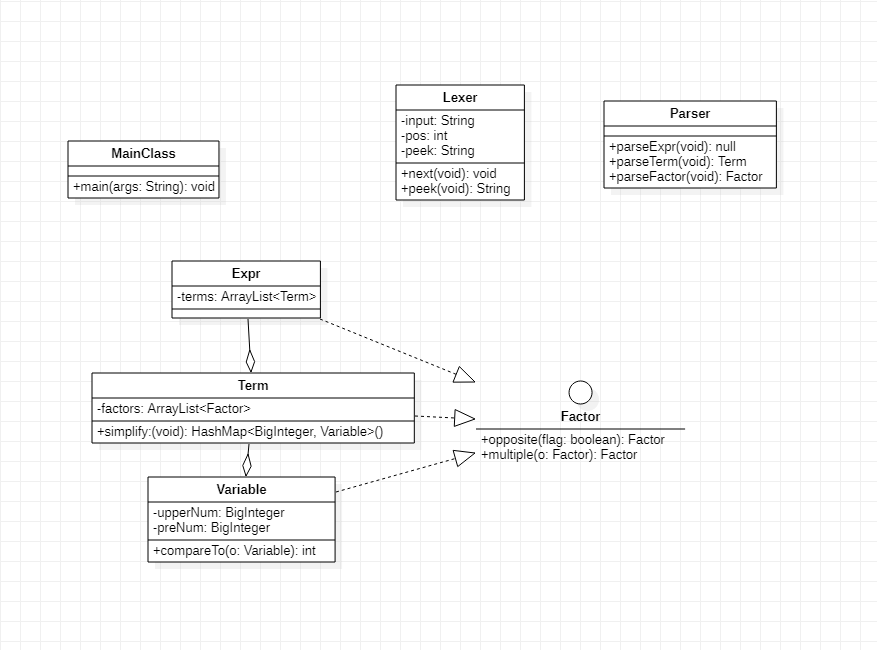
• Lexer: 负责解析输入字符串，将每一个元素解析出来供Parser对象进一步解析。

• Parser: 分层次解析Expr, Term, Factor的对象，构建数据间的关系。

• Factor: Expr和Variable的共同接口，从行为层次抽象，便于Term中统一管理。

• Expr: 表达式类，处于最高层次，同时可以降到最低层次进行递归。

• Term: 由乘号连接，处于中间层次。

• Variable: 只有系数与指数属性，处于最低层次，是最基本的对象。

• MainClass: 主类，控制流程，同时负责输入输出功能(设计不当，违背了单一职责原则)。

  数据层次的划分比较清晰，实现关系与聚合关系使用合理，但Lexer类完全可以放在Parser类中，因为解析表达式时，一个Parser是唯一使用一个对应Lexer对象的，这也是Lexer类的唯一作用。这两个类可以形成组合关系，连接更紧密，这一点当初未能考虑到。

第二次作业

  第二次作业对我整体设计的冲击十分大，sin和cos的加入完全否认了我之前为了偷懒创建的以x系数为key，Variable为对象的简单模式，不得不进一步复杂化Term的属性和方法，而这也很大程度上违背了开闭原则，属于某种程度上的重构了。考虑到sin和cos与x的相似性，即都有系数和指数，唯一的区别是前者的内部多了一部分。因此我分别实现了sin和cos类，继承Variable。因此整体看来，数据层次的划分基本延续了第一次作业的设计。为什么不将sin和cos再抽象出一个公共的类呢？因为当时偷懒觉得只有两个类分别实现也不复杂。但这种设计不仅可扩展性差，而且当我在具体实现时才发现分别实现sin cos导致我在创建新对象时不得不用getClass()条件判断当前对象是sin还是cos，格外繁琐。虽然这个问题可以用创建对象的一些设计模式解决，但我功力不够也不敢尝试，只能将就着了。

  这次设计最大的亮点在于往各个层次中加入低层次对象的同时进行合并同类项，这样就相当于加入元素时完成了计算，能很大地优化时空复杂度。比如，向Expr中加入一个Term对象时，直接从Expr的容器中寻找是否有和当前对象equal的对象(前提是我为各个类重写了equals方法)，如果有，便进行合并，没有便加入容器。具体实现方式如以下代码所示。

public void addTerm(Term term) {
    for (Term thisTerm : terms) {
        if (thisTerm.equals(term)) {
            // 如果是同类项便将系数相加
            thisTerm.setPreNum(thisTerm.getPreNum().add(term.getPreNum()));
            return;
        }
    }
    terms.add(new Term(term));
}

  为了方便，我还是使用的ArrayList，循环遍历查找。后来经过反思，我认为可以直接为Term类重写compareTo方法(毕竟已经重写了equals方法)，用HashSet存储项，加入项时判断集合内是否已包含当前项来决定合并还是加入集合，这样的实现方法效率会更高。

  另一个新增功能是函数的实现。其实我最初的想法也是将函数视为因子，在解析过程中进行计算后返回因子类型。但随着更多的具体思考，我面临一个问题：函数的定义需要创建对象，而解析时必然需要根据函数的定义来代入实参获得计算后的对象，那么这些函数定义对象由谁创建，又应该交给谁保管？当初我认为无论将这些对象放在哪个类里都似乎有点超越权限职责，进而选择最暴力的表达式替换进行处理。但在第三次作业时，我又认真思考了这个问题，发现将函数定义对象交由Parser，即解析类，去保存调用既自然又合理，因为这个对象本身需要解析表达式的成分，那么保管一些解析所必须的对象也是职责之内。因此我在第三次作业中成功替换成了边解析边代入的模式。

  之前提到，我这次对函数的处理是表达式替换，因此我特意实现了专门的输入类，去处理函数的字符串替换，具体实现起来也遇到较多bug，这些内容会在后面专门部分提及。

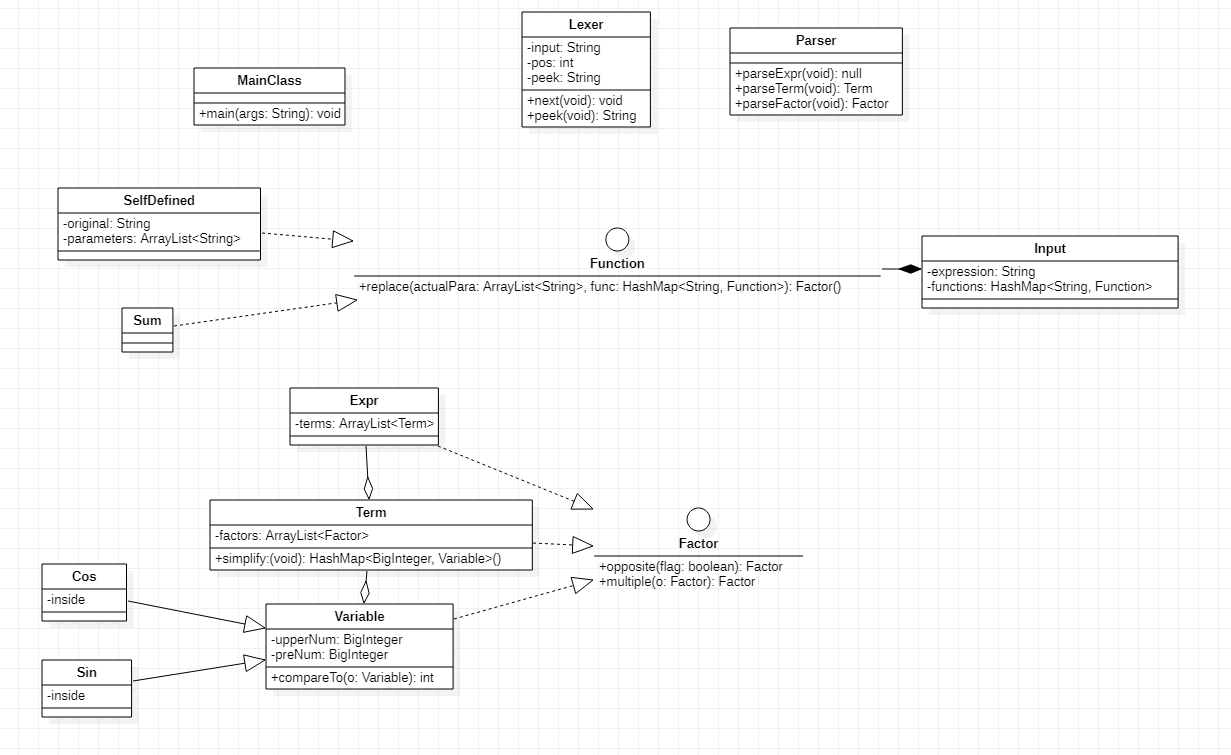
• Sin: 继承Variable，是一种变量，区别在于内部多了一个表达式对象。
• Cos: 同Sin。
• Function: 接口，抽象出函数公共的替换实参方法，本次设计时返回全部替换后的表达式字符串，便于统一管理自定义函数和求和函数。
• SelfDefined: 自定义函数，具有表达式和参数属性，实现了Function接口
• Sum: 求和函数，实现了Function接口。
• Input: 输入类，完成所有函数的替换功能，将字符串传递给后续解析。
• Expr: 相较于第一次作业修改了addTerm方法，加入项时进行同类项合并，加入了各种三角函数优化方法。
• Term: 修改了addFactor方法，加入因子是进行计算。

  相对第一次作业，三角函数继承了Variable并新增了内部表达式属性，实际意义为将三角函数和变量统一为一个层次，便于统一解析。主要缺点是为能进一步抽象出三角函数类供sin和cos继承，导致可复用性变差。函数这一块抽象出了函数接口，由自定义函数和求和函数实现字符串替换方法。函数和输入类构成组合关系，仅在输入时便彻底完成所有函数替换。这种设计虽然思路直接，处理起来比较纯粹，但没有很好地体现函数个体作为因子的层次化思想，有违面向对象设计理念。

第三次作业

  第三次作业对我而言十分轻松，因为我之前就设定sin和cos里面的元素是个表达式，而非单纯按照第二次作业的要求设定为常数或者x的次方，因此这一功能已经实现。剩下的函数递归调用问题也在我修改了边解析边代入的模式后顺带实现。所以第三次作业的整体架构基本等同于第二次作业，甚至代码量还减少了许多。主要额外处理的部分是当三角函数内部是项或者表达式因子时需要额外加括号。这里我是稍微修改了各个数据类的toString方法，比如项如果包含多个因子就最终套上括号，表达式如果有多个项或者项toString后两边有括号则需要套括号。

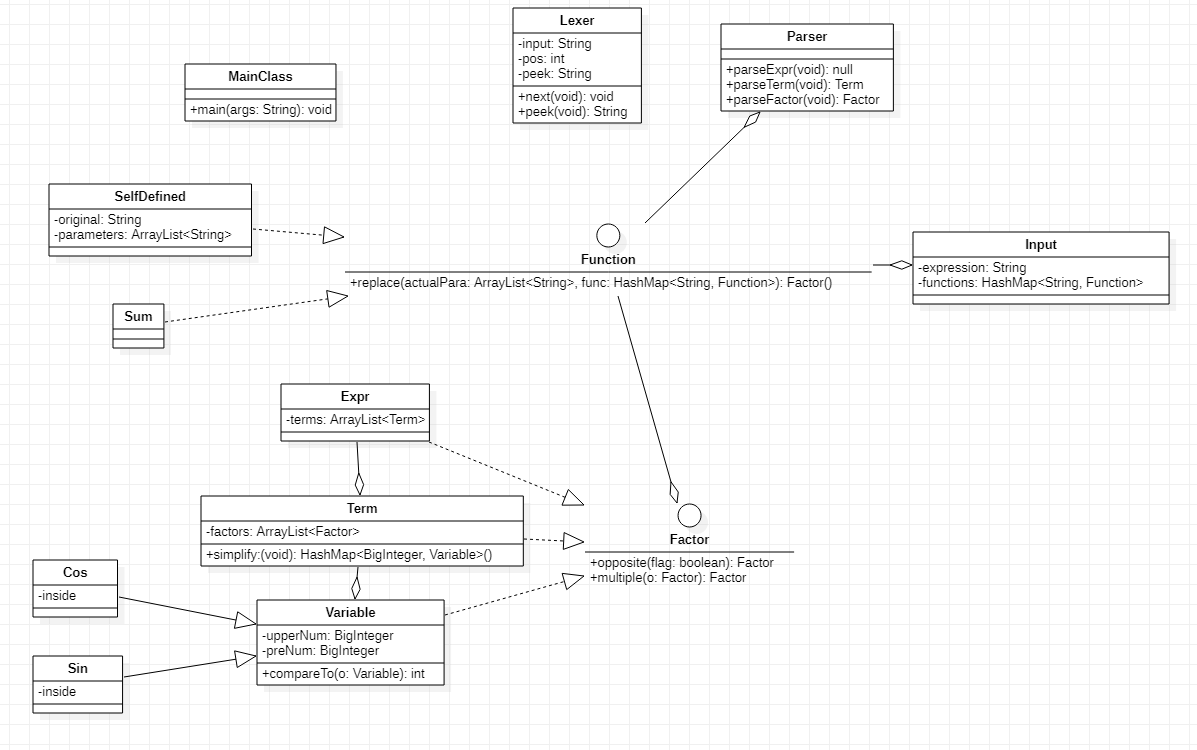
  由于第三次作业相较于第二次作业的主要变化在于函数，这里主要解释有关函数处理的变化。

  首先有输入类负责解析出函数名、参数个数、参数顺序等信息，创建出具体函数对象并交由Parser类保管，供解析表达式时遇到函数使用。因此，Function与Parser和Input构成聚合关系。这种设计体现出函数的个体性，将函数调用看做是函数本身的一个方法，返回Factor对象。

---

优化部分

  优化是获得性能分的关键，也是功能性正确后的另一重大任务。

  第一次作业最终的输出单纯是一多项式，前文也提到可以设计出简单的系数->对象的键值对去合并所有同类项，因此没有什么优化的空间。

  但自从第二次作业引入了三角函数，优化便成了一座大山。

  首先自然是sin(0)和cos(0)的优化，因为这两个因子可以替换为常数，能极大地缩短长度，是不得不优化的部分。这里值得注意的是如何进行常数替换。sin(0)为0，与其相乘的项最终都是0，因此可以直接将表达式中包含的这个项直接删除。cos(0)是1，即在项的乘法中没有贡献，因此可在项中将cos(0)给移出。删除便带来问题：java中for-each语句不支持正常删除，如果强行删除并继续遍历会带来越界问题。解决这个问题的方法有两种，一种是使用迭代器模式进行遍历，一种是使用循环调用这个优化方法的方式不断寻找可能的优化，找到一个删除后便返回，直到找不到存在的优化。第二种方式实现如下。

boolean flag = true;
while (flag) {
    flag = sin0AndCos0();
}

  其次是sin**2+cos**2的优化，两者相加等于1，也能极大地缩短长度。这个优化相对困难一点，因为需要两重循环比对表达式中的项，还要循环判断两个项的其他因子是否完全一样。我的第一想法是寻找存在的sin**2，为其匹配对应的cos**2，但是这样的简单想法无法合并高于2次的可能合并的情况，比如,sin**2*cos+cos**3。厉害的朋友告诉我可以寻找sin的任何高于2次的项，将其系数减2后以新的项去匹配其他cos系数减2的项，这样的方法能很好地解决高次项的合并问题。在表达式中，可以循环调用这个优化方法，直到没有优化的空间，便退出。但这种随便找两个就合并的贪心模式不一定能达到最优解，原因在于优化后便没有了反悔的可能。后来考虑使用动归，感觉类似选择个数的问题，需要使用状压，用二进制不同状态记录选择了哪些项(这里数据的大小也很适合状压)。然而，我总感觉这里不具有无后效性，子状态的最优并不一定能推到后续的最优，因为每个状态只能记录当前表达式，无法记录优化顺序(具体的思路也不太清晰，若有错误，恳请指正)。后来我还是选择了最容易最暴力的dfs，枚举所有优化顺序选择最短结果。但是这种暴力搜索在处理平方和的六次方展开式时便会因递归深度太深而难以计算出结果。考虑到状态的重复性，我又使用记忆化的方法，暴力使用HashSet记录访问过的表达式toString后的状态。若当前搜索的表达式在HashSet中有记录便直接返回。实现后的效果可以在1s左右计算出上述记忆化优化前计算不出的六次方平方和，有了很大的提升。其实记忆化后，面对更高次的复杂度，本身的时间消耗的增长速率相对于dfs直接的阶乘复杂度也有了很大的提升。

  其他诸如a-b*sin**2，a-b*cos**\2的优化类似上述平方和优化，不在此赘述。

  另一个较容易的优化是sin的二倍角。我的实现方式是在一个项中循环遍历sin和cos，取出最高次幂，再判断这个项的系数能不能分解出最高次幂个2，如果可以便进行合并，反之则放弃(因为个人感觉二倍角若不能完全化简反而会增加长度)。至于cos的二倍角实现起来相对复杂，需要考虑三种展开/合并方式，这种优化我也没有动力去实现，而这也导致我第三次作业部分性能分的丢失。

---

三次作业度量分析

  本次使用代码度量工具DesigniteJava来分析三次作业的结构。由于每次作业分析数据太多，这里不一一展示，仅列出具有代表性的数据重点分析。

第一次作业

  从数据分析可以看出，第一次作业整体代码量比较小，单个类的代码行数最多也只有79。此外，类的方法个数体量也很小，都不超过10个，平均应该在5个左右。LCOM(方法的内聚缺乏度)都小于等于0，基本满足了方法间的高内聚低耦合。数据层次的类FANIN和FANOUT比较多，表示互相调用次数多，相对而言耦合性更大。

  因此，整体而言，第一次作业的设计由于体量小，最终效果也中规中矩。数据层次类的耦合其实也符合本次单元作业层次化设计的理念，让不同层次的对象之间互相调用。其他数据处理类和流程控制类的耦合度都为0，利于复用和扩展。

第二次作业

  第二次作业的代码量很明显远大于第一次。这里列出几列关键数据。

Type Name	NOPM	LOC	LCOM	FANIN	FANOUT
Cos	6	39	0	3	2
Expr	18	365	0	6	5
Factor	0	4	-1	4	1
Sin	6	39	0	3	2
Term	16	223	0	3	6
Variable	10	69	0	2	2
Function	0	3	-1	0	0
SelfDefined	4	30	0	1	0
Sum	1	16	-1	0	0
Input	2	64	0	0	1
Lexer	3	46	0	0	0
MainClass	1	9	-1	0	1
Parser	6	103	0	0	2

  可以看出，某些类的代码量达到了几百行，方法个数也接近20个，而产生如此冗长的类的原因是三角函数的优化。这些优化需要多重循环的遍历和条件判断，每种优化方法我又单独提出复写，导致每种优化方法之间虽有相似之处却未抽象出公共方法，属于设计缺陷。和第一次作业相同，数据层次的类之间的耦合度依旧比较高。至于圈复杂度，Expr类中的优化方法毫无悬念地居于复杂榜首，数值在13左右。其余相对更复杂的是Parser类的因子解析方法，可能是因为具有一定的递归深度而且随着因子种类增加判断条件变多。

第三次作业

Type Name	NOM	LOC	LCOM	FANIN	FANOUT
Cos	6	39	0	3	2
Expr	19	405	0	6	5
Factor	2	4	-1	5	1
Sin	6	39	0	3	2
Term	16	260	0	3	6
Variable	10	69	0	2	2
Function	1	3	-1	0	0
SelfDefined	2	26	0	1	2
Sum	1	18	-1	0	2
Input	4	36	0	1	1
Lexer	6	67	0	4	0
MainClass	1	15	-1	0	4
Parser	9	137	0	4	5

  这次作业基本没什么修改，因此整体数据和第二次相差不大。由于稍微增加了一点优化，因此部分类的代码行数略有增加。由于应用了边解析边处理函数的方式，导致函数内部需要调用新的解析对象的方法，因此类之间的耦合度变高。圈复杂度也与上次作业相似，那些优化方法复杂度最高。

---

遇到的bug

自己的bug

  在课下完成作业的过程中，我个人遇到了许多bug，其中始终伴随我的是深浅克隆问题。

  对表达式层次化解析需要使用各种容器取存储更低层次的对象，因此我在一些类中使用ArrayList去存储。然而，在进行计算时，比如表达式的乘法，我的实现方式是两重循环遍历两个表达式的每个项，将其中一个项的所有因子加入到另一个项的容器中（因为项的所有因子只有乘法关系，所有因子存储于同一个容器中）。这种情况下，同一个因子会被重复加入不同项的容器中，然而真实我物理意义是这两个项包含的因子是不同的。这样的状态不仅违背了设计初衷，在需要合并同类项或进行表达式优化时，修改其中一个因子更是会导致其他毫不相干的项的改变，产生致命错误。

  意识到这一点后，我逐渐去为各个类实现深克隆，具体实现方法是创建新的构造方法，参数是需要克隆的对象，然后在构造方法中创建新的容器，将原对象容器中的每个元素再深克隆一份加入新容器中。这样循环递归下去，直到最底层的Variable类的属性只有两个BigInteger，属于不可变类型，直接等号赋值即可完成深克隆。底层完成克隆后再逐步向上返回，最终实现所需对象的深克隆。

  其次，我还在课下遇到一些细节bug，比如解析正负号不符合形式化表述的要求造成runtime error，对函数的实参替换不正确，表达式替换忘加括号……但很幸运，这些bug都在我的测试或和朋友们的讨论中及时发现并解决了。

  然而，有些bug就没有这么幸运了……

  在第二次作业中，房间的一位朋友锐利地找出我的一个bug：cos(0)前面有两个符号且紧挨着的是负号会出错。这个bug说来也巧，由两个地方的疏忽造成。首先是我对正负号的解析顺序由偏差。形式化表述明确说明cos前面不会有符号，因此，其前面的符号应该是属于更高层次的项的符号。然而我却将其解析给了cos这一更低层次。其实只有这一理解错误倒不会影响正确性，因为我的设计中，化简后的项有标准形式，即ax**bsin...cos... ，所有的常量最终会在第一项。但巧合的是我一时没想清楚，将对sin(0) cos(0)的优化放在了化简前面。这意味着在优化cos(0)时我还没有将其前面的系数放到第一项。于是我直接remove了cos(0)，其系数(-1)也被我顺便抹去，导致错误。此外，这个bug还导致我优化失败，比如(cos(0))，cos(0)在化简前还属于表达式因子，优化方法检测不到便不会对其进行替换。

  第三次互测，我的作业同样未能幸免，被一位同学hack。这次是三角函数里的加减表达式未加括号导致format error。说来惭愧，课下迭代第三次作业只想着乘法需要加括号，忘记了对加减的处理。

他人的bug

  互测中，我都是将所有人的代码下载到一个文件夹，用Python脚本不断运行寻找错误。但这种方式找到的bug都是很明显的bug（因为随机数据复现一些极端情况bug的概率很小），比如第三次中有人的三角函数里是一个项时便会解析错误，抛出异常、第一次作业中有人解析连续的正负号会出错。更多有效的bug还是通过手动尝试典型数据找到的，比如sum爆int，sum里上下限是负数会因为处理时没打括号出错等。这些bug都是由于对项目需求分析不到位造成的，看似细节，实则重要。在实际开发中，不能忽视每一种可能遇到的状态，要精准处理所有情况。

---

测试方面

  测试是课下必不可缺的一部分，因为完成作业后，即使通过了中测，也很难保证自己的项目有一定的正确性。这三次作业中，我分别实现了数据生成器与对拍脚本。数据生成的方法类似作业，将表达式层层解析，从低到高toString获得最终的表达式。后面的函数也是额外实现类，在项中加入。对拍脚本用Python实现，用subprocess模块调用命令，用sympy模块判断表达式是否等价。

# 运行java项目方法
def get_data(name, flag, main_name, expr) -> str:
    class_path = "E:/MyOO/" + name + "/out/production/" + name
    if flag: # 数据生成器不需要jar包，额外判断一下
        jar = ";E:/MyOO/jarLib/official_3.jar"
    else:
        jar = ";"
    command = "java -Dfile.encoding=UTF-8 -classpath " + class_path + jar + " " + main_name
    p = subprocess.run(command, input=expr, stdout=subprocess.PIPE, encoding="UTF-8")
    return p.stdout

# 比较答案是否等价
my_ans = get_data("task3", True, "MainClass", expr).split('\n')[1]
other_ans = get_data("other" + str(num), True, name, expr).split('\n')[1]
if sympy.Symbol.equals(sympy.simplify(my_ans), sympy.simplify(other_ans)) == False:
    print("wrong " + str(num))
    # 如果错误则将数据备份下来
    f = open(backup_path + str(num) + "_" + str(times) + "backup.txt", "w")
    f.write(bak)
    f.write(other_ans)
    f.close()

在互测中也可以用脚本一起比对，循环调用评测方法去发现bug。自动评测固然好，但生成的数据缺乏典型性，自己测试典型数据也是非常重要的。比如测试sum的上下界会不会爆int，连续符号的处理会不会错，三角函数的一些优化会不会导致bug……

---

心得与感悟

  经过第一单元的训练，我开始习惯面向对象这门课程的节奏。但是要说对面向对象思维的理解，我还是只触及了皮毛。拿到一个全新的任务，我很难自己设计层级架构，很难自己为所需的类分配各自的任务。最近了解了设计模式、设计原则有关内容，更是感觉面向对象无涯，诸多方法只可叹其妙，不知如何化为己用。还得多学多练！希望在今后单元的学习中，我能不断深化对面向对象设计的理解，能够自如地分解需求，让一个个对象自动浮现在脑海！