搜索(八皇后) 洛谷P1219:
//搜索的实现。 //优化dfs1。 //八皇后。 //n个皇后在不在同一条直线或同一条斜线,一共多少方案。 #include<iostream> #include<cstdio> using namespace std; int n,ans=0; int pos[maxn];//pos[i]代表第i行的皇后放在了第pos[i]列。 void dfs(int now){//现在要去尝试放第now行的皇后。 if(now>n){ ans++; return; } for(int j=1;j<=n;j++){//第now行的皇后放在第j列。 bool able=true; for(int i=1;i<now;i++){//枚举第i行的皇后。 if(pos[i]=j||abs(now-i)==abs(j-pos[i])){ able=false; break; } } if(able){ pos[now]=j; dfs(now+1); } } } int main(){ n=13;//3.68s。 dfs(1); cout<<ans<<endl; return 0; }
优化dfs2。
判断第i行、第i条斜线上有没有皇后。
斜线=i+j-1>。
#include<iostream> #include<cstdio> using namespace std; int n,ans=0; int pos[20];//pos[i]代表第i行的皇后放在了第pos[i]列。 bool col[20];//col[i] 代表第i条的直线有没有皇后。 bool xie1[50];//xie[1] 代表第i条从左上到右下的斜线有没有皇后。 bool xie2[50];//xie[2] 代表第i条从右上到左下的斜线有没有皇后。 void dfs(int now){//现在要去尝试放第now行的皇后。 if(now>n){ ans++; return; } for(int j=1;j<=n;j++){//第now行的皇后放在第j列。 int ibx1=j-now+n;//从左上到右下的斜线编号。 int ibx2=now+j-1;//从右上到左下的斜线编号。 if(!col[j]&&!xie1[idx1]&&!xie2[idx2]){ pos[now]=j; col[j]=xie1[idx1]=xie2[idx2]=true; dfs(now+1); col[j]=xie1[idx1]=xie2[idx2]=false; } } } int main(){ n=13;//0.6141s。 n=14;//3.494s。 dfs(1); cout<<ans<<endl; return 0; }
图论:
图的概念 由点和边构成的元素
边:如果边都有方向 我们叫它有向图 没方向叫无向图
一、图的一些基本概念:
1.度:一个顶点连了几条边 就是它多少度
2.有向图里的入度和出度:连向自己的度就是入度 往外连得就是出度
3.有向图里的自环:既是入度又是出度
4.路径:只要沿着边走叫做路径 如:1 -> 2 -> 3 -> 2 -> 1
5.简单路径:不能走重复点和边的路径 如:1 -> 2 -> 3u
6.环:起点等于终点的路径(绕起来) 如:1 -> 2 -> 1
7.简单环:起点等于终点且保证除起点和终点外不经过重复的点和边
图的分类方式:1.树:无向、无环、连通(任意两个点之间都可以互相走到)
如果有一个n个点的树,它一定会有n - 1条边
2. 森林:无向、无环(很多棵树)形象!
3.有向树:无环、连通
{
外向树:如果所有边都指向外边
内向树:如果所有边都指向一点
注意:有可能一棵树既是外向树又是内向树!
}
4.章鱼图:无向、连通、有环且只有一环
章鱼图的每一个点向往外延伸 一定是一棵树。如果一个章鱼图有n个点,它就一定有n条边
章鱼图想要变成树,只需要去掉环上的一条边
一棵树想要变成章鱼图,只需加一条边
5.DAG ——> 有向无环图
6.二分图(无向图) --> 能够把所有的边分为两部分不要求联通
见图:
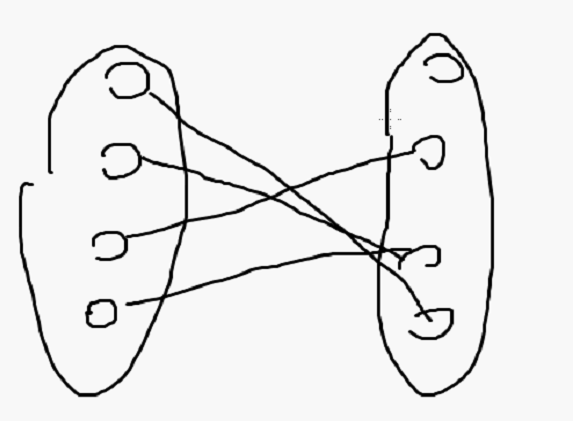
树和森林一定是二分图
判断:没有奇环(即奇数个顶点组成的环) 就是二分图
二、代码实现存图
1.邻接矩阵存图
int z[101][101]; //z[i][j] 代表i到j那条边的长度 int main(){ cin >> n >> m; for(int i = 1; i <= n; i++){ int s,e,d; cin >> s >> e >> d;//起点为s,终点为e,长度为d z[s][e] = d;//有向图 //z[e][s] = d; 无向图 } }
坏处:内存消耗比较大
好处:简洁、快(因为只要知道i到j的那条边的信息 O(1))
2.边表存图
vector< pair<int,int> > z[maxn]; //z[i]:代表 所有以i为起点的所有边 //z[i][j] :代表所有以i为起点的第j条边 //z[i][j].forst:代表i为起点的第j条边的终点 //z[i][j].second: 代表i为起点的第j条边的起点 void add_edge(int s, int e, int d){ z[s].push_back(make_pair(e,d)); //push_back:向vector的末尾添加一个元素 } int main(){ cin >> n >> n; for(int i = 1; i <= n; i++){//添加一条从s出发,到e 长度为d的边 int s,e,d; cin >> s >> e >> d; add_edge(s,e,d);//添加一条边 STL函数 add_edge(e,s,d);//无向图 } for(int i = 1; i <= n; i++) for(int j = 0; j < z[i].size();j++){ int e = z[i][j].first; int d = z[i][j].second; //代表当前的边 是从i开始的第j条边 终点为e 长度为d } }
优点:改善了上一种方法的内存
缺点:慢
三、解决一些问题
1.一张图 有n个点 me 条边 并且是一张无向图 请判断是否是二分图(二分图染色)
思路:染色法从一号点开始 将其染色为1 与它相邻的点应当是第二部分 ;与第二部分相邻的点就是第一部分。如果能够成功将所有的点都染色 就是二分图 如果一个点的两边的点颜色相同就不是二分图
注意:这里其实有一个坑,我们从一号点开始 如果我们的图不连通就无法找到所有点,所以需要枚举
vector<int > z[maxn]; //z[i]:代表 所有以i为起点的所有边 //z[i][j] :代表所有以i为起点的第j条边 //z[i][j].forst:代表i为起点的第j条边的终点 //z[i][j].second: 代表i为起点的第j条边的起点 void add_edge(int s, int e){ z[s].push_back(e); //push_back:向vector的末尾添加一个元素 } int col[maxn]; //col[i] == 0 代表还没有染色 //否则代表第i个点的颜色 int main(){ cin >> n >> n; for(int i = 1; i <= n; i++){//添加一条从s出发,到e 长度为d的边 int s,e; cin >> s >> e; add_edge(s,e);//添加一条边 STL函数 add_edge(e,s);//无向图 } for(int i = 1; i <= n; i++){ if(col[i] != 0) continue; col[1] = 1; queue<int> q;//可以改变周围点颜色的点 q.push(1); while(q.size()){ int i = q.front(); q.pop(); for(int j = 0; j < z[i].size(); j++){ int k = z[i][j]; //i -> k 的一条边 if(!col[k]){ col[k] = 3 - col[i]; q.push(k); } else{ if(col[k] !== col[i]){ cout << "不是二分图!" << endl; exit(0); } } } } } cout << "是二分图 !"<< endl;//顺利完成整个程序 return 0; }
2.拓扑排序(针对DAG)
保证排完序之后原图当中存在的边都是从左向右指的,叫做拓扑排序。
如果一个点的入度为零 应把它放在最前面 把每次入读为0的点更新实现:
vector<int > z[maxn]; //z[i]:代表 所有以i为起点的所有边 //z[i][j] :代表所有以i为起点的第j条边 //z[i][j].forst:代表i为起点的第j条边的终点 //z[i][j].second: 代表i为起点的第j条边的起点 void add_edge(int s, int e){ z[s].push_back(e); //push_back:向vector的末尾添加一个元素 } int col[maxn]; //col[i] == 0 代表还没有染色 //否则代表第i个点的颜色 int in[maxn];//代表i点的入度 是多少 int main(){ cin >> n >> n; for(int i = 1; i <= n; i++){//添加一条从s出发,到e 长度为d的边 int s,e; cin >> s >> e; add_edge(s,e);//添加一条边 STL函数 in[e] ++; } int cnt = 0; for(int i = 1; i <= n; i++) if(in[i] == 0) resault[++cnt] = i; for(int i = 1; i <= n; i++){//当前要取出的拓扑排序的结果中的第i个点 int p = result[i]; for(int j = 0; j < z[p].size(); j++){ int q = z[p][j];//p -> q的边 in[q] --; if(in[q] == 0) result[++cnt] = q; } } return 0; }
插播一点小概念:每个节点在第几层叫做这个节点的深度
祖先:在i上面的节点
lca(i,j) = i 和j的最近公共祖先
Q;给出树 求出lca(i,j)
vector<int > z[maxn];
//z[i]:代表 所有以i为起点的所有边
//z[i][j] :代表所有以i为起点的第j条边
//z[i][j].forst:代表i为起点的第j条边的终点
//z[i][j].second: 代表i为起点的第j条边的起点
void add_edge(int s, int e){
z[s].push_back(e);
//push_back:向vector的末尾添加一个元素
}
void dfs(int i, int j){//i 的父节点是j
f[i] = j;
depth[i] = depth[j] + 1;
for(int k = 0; k < z[i].size();k++){
int l = z[i][k];//这条边是从 i -> l的边
if(l != j) dfs(l,i);
}
}
void get_lca(int p1, int p2){
while(p1 != p2){
if(depth[p1] < depth[p2]) swap(p1,p2);
p1 = f[p1];
}
return p1;
}
int depth[maxn], f[maxn];//深度 父节点
int main(){
cin >> n >> n;
for(int i = 1; i <= n; i++){//添加一条从s出发,到e 长度为d的边
int s,e;
cin >> s >> e;
add_edge(s,e);//添加一条边 STL函数
add_edge(e,s);
}
dfs(1,0);
return 0;
}
优化:倍增求lca
int depth[maxn], f[maxn][20];//深度 从i vector<int > z[maxn]; //z[i]:代表 所有以i为起点的所有边 //z[i][j] :代表所有以i为起点的第j条边 //z[i][j].forst:代表i为起点的第j条边的终点 //z[i][j].second: 代表i为起点的第j条边的起点 void add_edge(int s, int e){ z[s].push_back(e); //push_back:向vector的末尾添加一个元素 } void dfs(int i, int j){//i 的父节点是j f[i][0] = j; for(int k = 1; k < 20; k++){ f[i][k] = f[f[i][k - 1] ][k - 1]; } depth[i] = depth[j] + 1; for(int k = 0; k < z[i].size();k++){ int l = z[i][k];//这条边是从 i -> l的边 if(l != j) dfs(l,i); } } void get_lca(int p1, int p2){ //把p1 p2深度调整成一样的 else if(depth[p1] < depth[p2]) swap(p1, p2); for(int i = 19; i >= 0; i--) if(depth[f[p1][i]] >= depth[p2]) p1 = f[p1][i]; if(p1 == p2) return p1; for(int i = 19; i >= 0; i--) if(f[p1][i] != f[p2][i]) p1 = f[p1][i], p2 = f[p2][i]; return f[p1][0]; } int main(){ cin >> n >> n; for(int i = 1; i <= n; i++){//添加一条从s出发,到e 长度为d的边 int s,e; cin >> s >> e; add_edge(s,e);//添加一条边 STL函数 add_edge(e,s); } dfs(1,0); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号