信息的表示(三)

信息的表示(三)

浮点数的表示

要理解浮点数在计算机中的表示，我们先回到二进制中整数的表示，不考虑有符号的情况。二进制整数中从低位到高位每一个位的权值逐个翻倍。一个\(k\)位的无符号二进制数最低为权值位\(2^0\)，最高位权值位\(2^k-1\)。直观上考虑二进制小数，则权值应从\(2^0\)开始往下逐个除2。事实也确实如此，例如：

\[d_md_{m-1}...d_1d_0.d_{-1}d_{-2}...d_{-n} \]

这个数值描述的大小为\(d = \sum \limits ^m _{i=-n} 2^i * d_i\)。

上述是在我们直观理解下的二进制带小数的表示，这样的表示存在许多的缺陷，例如不能够表示足够多的小数位数，每次想要增加一个小数位数都要在后面补充一位，想要表达小数点后100位则要在小数点后面添加100个数字。而且这样的表示方法有许多时候不能够表达一些数字，例如\(\frac 1 3\)这样的无限循环小数不容易直接表示。为了解决以上这些缺陷，在标准的二进制表示用了与直观上相似的表示方式。

IEEE浮点表示

IEEE浮点标准使用了\(V=(-1)^s * M * 2^E\)的形式来表示一个浮点数

s : 符号(sign), 符号位，正时为0，负时为1，对于0特殊处理。

E：阶码(exponent)，对浮点数进行加权，每一位也就是2的E次幂。

M：尾数(significand)，是一个二进制小数，范围是0 ~ 1-e或者1 ~ 2-e。

单精度浮点数中从左到右s占用1位，E占用8位，M占用23位，总共占用32位。双精度浮点数中从左到右s占用1位，E占用11位，M占用52位。

很明显单精度浮点数和双精度浮点数在表达方式上没有区别，只是精度不同。

浮点数中使用了偏置(bias)形式表示的有符号整数。

非规格化值

当阶码全为0时，所表示的数是非规格化形式。在这种情况下，阶码值定义为\(E=1-Bias\)，尾数值定义为\(M = f\)。

Bias：一个等于\(2^{k-1}-1\)的值，单精度中为127，双精度中为1023

f：表示尾数域中的值

规格化值

当阶码不全为0也不全为1时，所表示的值是规格化形式。在这种情况下，阶码值定义为\(E=e-Bias\)，尾数值定义为\(M=1+f\)。

e：表示阶码域中的值

这种情况下对单精度满足\(-126 < E < 127\)，对双精度满足\(-1022 < E < 1023\)。

特殊值

当阶码全为1时，所表示的值时特殊值。在这种i情况下，当\(s=0\)时是\(+\infin\)，当\(s=1\)时是\(-\infin\)。当尾数域中非0时，结果值称为"NaN"，也就是“Not a Number”的所借。

上述我们可以用这样一张图更清晰的概括：

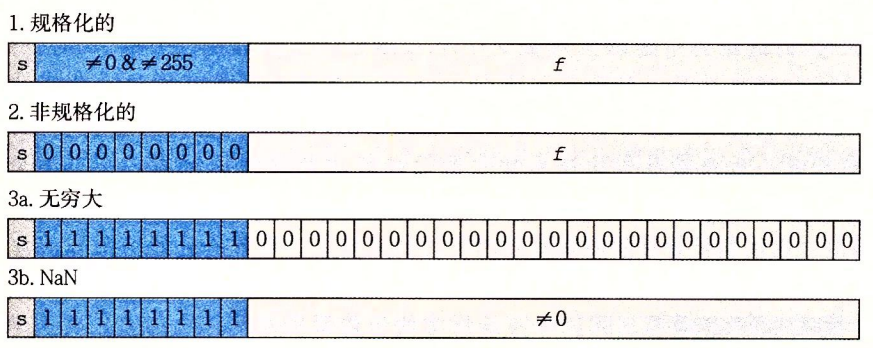
可能你会疑惑为什么要用这些这么反直觉的定义方式，实际上这些看上去反直觉的定义方式是很聪明的做法，它提供了一种很流畅的表达方式。以8位的浮点格式作为示例，其中阶码为4位，尾数为3位。

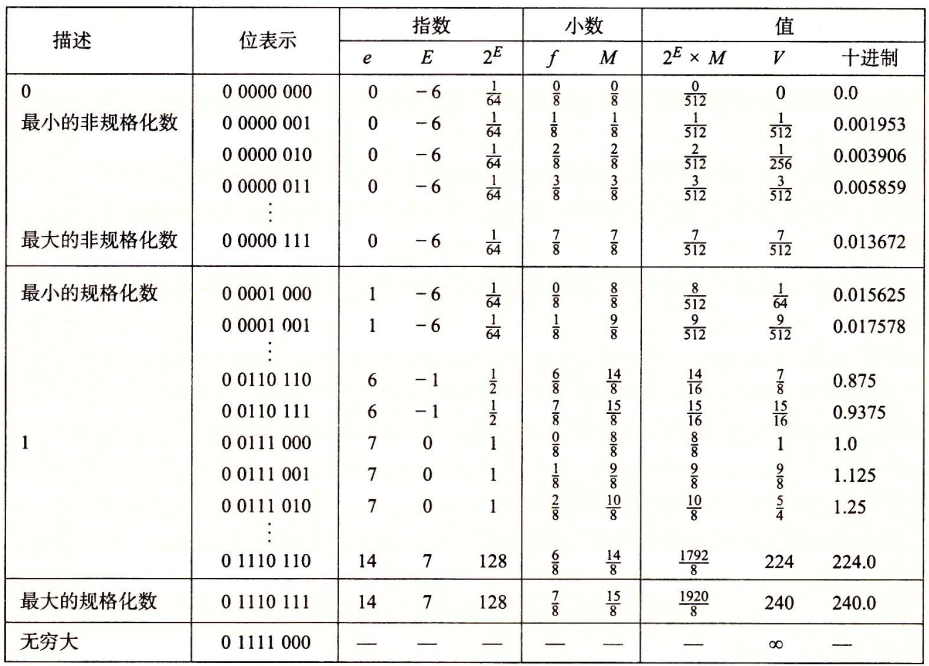
舍入

前面我们已经提到过，浮点数的表示方式精度上受到了限制，有许多的小数都不能够准确的表述，例如\(\frac 1 3\)只能够取一个近似值，舍入便提供了求近似值的许多方式。舍入方式由主要4种，分别是向偶数舍入、向零舍入、向下舍入、向上舍入。

向偶数舍入：将数字向上或者向下舍入，使得结果的最低有效数字是偶数，在二进制中用0表示偶数，1表示奇数

向零舍入：把正数向下舍入，把负数向上舍入

向下舍入：把正数和负数都向下舍入

向上舍入：把正数和负数都向上舍入

舍入中很常见的一个问题便是舍入结果后是大还是小，如果我们总是将一组数字向下舍入，那么摄入后的这组数的平均值相对原数字的平均值要更小，相反向上舍入则要更大。向零舍入也有相似的结果。这中间存在统计偏差，而向偶数舍入减小了这种偏差。这与十进制中的四舍五入的思想是一样的，只不过在二进制中低位变成了0，高位变成了1而已。

浮点运算

在了解了浮点数的表示方式后，我们很容易可以看出浮点数的运算和整数的运算本质上并无不同。只是在浮点数的运算中先对小数部分进行四则运算，再对阶码部分进行运算，分别运算完成再将结果组合就得到了最终的解，同样要在浮点数中处理溢出的问题，这与整数运算中也是相似的。只是在浮点数中溢出后将会使用NaN表示，而不是像无符号溢出后得到了一串反直觉的数字。

还有一个问题需要说明，IEEE的浮点数标准并不在各个语言中完全适用，C语言标准中并没有要求机器使用IEEE浮点数，所以也并没有标准的方法来改变舍入方式来得到特殊值。这在工业界同样容易引发许多潜在的问题，甚至已经因为这类问题导致了巨大的经济损失。