经验风险最小化

学习理论：

• 偏差方差权衡（Bias/variance tradeoff）
• 训练误差和一般误差（Training error & generation error）
• 经验风险最小化（Empiried risk minization）
• 联合界引理和Hoeffding不等式（Union bound & Hoeffding inequality）
• 有限与无限假设类的讨论（Discuss on finite and infinite hypothesis class）

 

一、偏差方差权衡

1. 偏差与方差

     回顾之前在讨论线性回归问题时，通常存在以下三种情况：

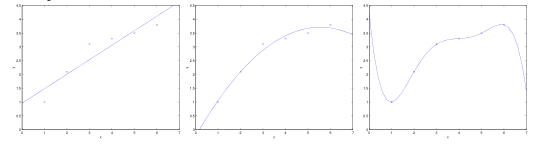
• 图1，用一条直线拟合一个呈现二次结构的散点，无论训练样本怎样增多，一次函数都无法准确地表示出二次函数。我们认为它具有高偏差（high bias），表现出欠拟合（underfit）。
• 图3，用一条五次多项式函数来拟合数据，对于数据的结果，得到的仍然不是一个好的模型，算法拟合出了数据中的一些奇怪规律。我们认为它具有高方差（high variance），表现出过拟合（overfit）。
• 图2，用一条二次函数来拟合数据，很显然能够匹配数据集合的一般规律。

     偏差与方差之间存在某种平衡。如果模型过于简单且参数较少，它可能有高偏差（低方差）；相反，如果模型过于复杂且参数众多，它可能有高方差（低偏差）。它们之间究竟存在怎样的关系呢？为了说明这个问题，先要提出一个更为一般的机器学习模型——经验风险最小化，在正式介绍该模型之前，需要对两个引理有所了解来帮助理解。

 

2. 两个引理

   为了解释偏差方差权衡现象，需要引出两个引理：联合界引理和Hoeffding不等式。

 （1）联合界引理

  

    这个引理常作为概率论的公理，k个事件中任意事件发生的概率最多为每个事件独立发生的概率之和。其中，事件可能发生，也可能不发生。

 （2）Hoeffding不等式

   

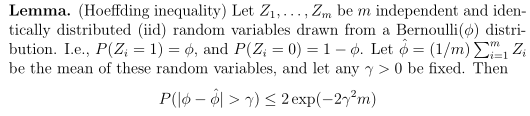
     这个引理在学习理论中也称为Chernoff边界（Chernoff bound），给出了一种估计伯努利随机变量均值时，错误概率的上界。关于这个上界有个很有意思的结论：随着样本数目m增大，高斯分布的凸性会随之收缩，也就是高斯分布的尾部会变小，中间隆起。举个例子，当你投掷一枚两面的硬币，人像面朝上的概率为Φ，在投掷m次（m足够大）后，计算人像面朝上的次数是一种很好的估计Φ值的方法。

 

3. 两个误差

    介绍两个学习理论中十分重要的概念：训练误差与一般误差。

 （1）训练误差

    考虑二元分类y∈{0,1}，给定训练集合S={(x⁽ⁱ⁾,y⁽ⁱ⁾);i=1,2,...,m}，训练样本服从独立同分布D，对于一个假设函数h，我们定义训练误差（Training error），也叫作经验风险（empirical risk）或经验误差（empirical error）：

   

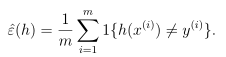
 （2）一般误差

   一般误差（Generation error）定义为：

 

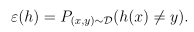
   它表示当从服从分布D的样本集合中取出一个样本(x,y)，假设函数h将会分类错误的概率。

 

4. 经验风险最小化

   以线性分类器为例，它的假设函数可以写成：

   

   拟合参数θ的一个方法是求解目标函数使训练误差最小。

  

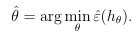
   这个过程被称作经验风险最小化（ERM-empirical risk minimization），它是简化的机器学习模型，逻辑回归和支持向量机可以看作为这个非凸优化问题的凸性近似。

 

二、假设类

1. 假设类的定义

     假设类（hypothesis class）为学习算法建立的所有分类器的集合。如线性分类器中，假设类H是输入范围X上所有分类器的集合；在神经网络中，假设类H是由一些神经网络结构表示的所有分类器的集合。

     线性分类器的假设类H为：

     

     经验风险最小化要做的是给定训练集合，从这k个函数中选取一个使得训练误差最小：

   

 

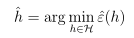
2. 有限假设类情形

    首先考虑有限假设类的情况，H={h₁,...,h_k}为有k个假设函数的假设类，也就是由k个从X映射到{0,1}的函数组成。接下来，要证明一般误差与最小误差之间是有上界的，简单地说，当训练误差很小时，一般误差也不会很大。

    证明策略：

• 训练误差是一般误差很好的估计；
• EMR输出假设的一般误差存在上界。

    证明过程：

（1）一致收敛概率界：

     a. 固定假设成立

• 前提条件：考虑一个假设类H中的任意固定的假设h_i∈H，定义服从伯努利分布D的随机变量Z=1{h_i(x)≠y}，表示第i个假设函数对样本错误分类的指示函数的值，其中Z_j=1{h_i(x^(j))≠y^(j)}。那么P(Z_j=1)=ε(h_j)，表示由分布D产生一个训练样本，假设对该样本错误分类的概率，也就是假设h_j的一般误差。故Z_j为一个伯努利随机变量，均值为ε(h_j)。ε(h)为随机变量Z（或Z_j）的期望值，训练误差为m个独立同分布伯努利随机变量Z_j的平均值，每个样本都是由均值为一般误差ε(h_j)的伯努利分布生成。

      

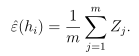
• 利用Hoeffding不等式可以得到：

      

       上式说明，给定一个假设h_i，训练误差与一般误差之间差异大于γ的概率有上界，即训练误差将会以很大的概率接近于一般误差。当m很大时，训练误差与一般误差之间的差异就很小。但是到目前为止，只证明了针对某个固定假设，两种误差之间的差异存在上界。由于最终我们要证明训练误差是一般误差很好的估计，故还需要证明在整个假设类H上任意一个h都满足这个条件。

      b. 任意假设成立

       假设Ai表示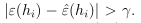的事件，已经证明对于任意的Ai，

       利用联合界引理可以得到：

       

      同时用1减去两边得到：

     

      上式说明，在不小于概率的情况下，对于假设类H中的所有hi，两个误差之间的差异将会在γ之内，这就是一致收敛（uniform convergence）。当m很大时，所有的训练误差将收敛于一般误差，即所有训练误差与一般误差都十分接近。

 

（2）样本复杂度界：

      给定γ和δ，m的值是多少？

      

      求解m的值得：

       

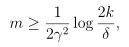
      只要样本数目m大于上式，对于任意的假设h，就能保证训练误差与一般误差之间的差异都在γ之内的概率至少是1-δ，称为样本复杂度界（Sample complexity bound）。

      m与logk呈正比，而logk增长的十分缓慢，随着k的不断增大，样本数目不会有太大的提高。

 

（3）误差界：

       固定m和δ，求解γ的值。至少在1-δ的概率下，对于所有假设类中的假设有：

      

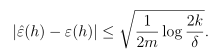
      γ的值为不等式右边的值

 

     假设一致收敛成立，所有h∈H，都满足：

    

     接下来要推导出H中具有最小训练误差假设的一般误差。并定义h^*，H中具有最小一般误差的假设。

     

     

     h^*是最理想的情况，学习算法就算再好也不会比h^*好，因此将学习算法与之比较是有意义的。

     

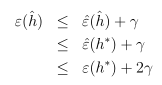
     定理：令H为有限的假设类，|H|>k，令m和δ固定，至少在1-δ的概率下，我们有：

    

     设γ的值为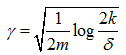，由一致收敛结果，至少在1-δ的概率下，ε(h)至少比ε(h^*)要高2γ。这个结论可以很好地帮助我们量化偏差方差权衡的问题。

     如果选择更复杂的目标函数或更多特征的类H’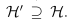，例如，将线性假设类换成二次假设类，假设类中最好的假设只可能更好，不等式右边的第一项（偏差bias）会减小，但代价是k会增加，从而第二项（方差variance）增加，这就是偏差方差权衡，可以用下图更具体的描述。

    

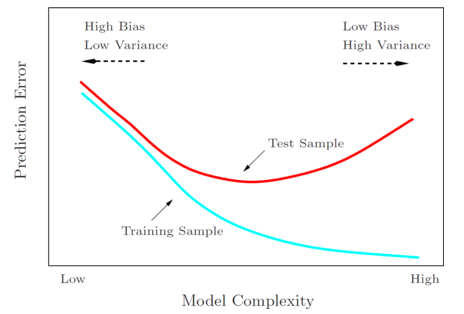
      随着模型复杂度（如多项式的次数、假设类的大小等）的增长，训练误差逐渐降低，而一般误差先降低到最低点再重新增长。训练误差降低，是因为模型越复杂，对于训练集合的拟合就越好。对于一般误差，最左边的端点表示欠拟合（高偏差），最右边的端点表示过拟合（高方差），最小化一般误差时，一般倾向于选取中间的模型复杂度，最小一般误差的区域。

 

     最后介绍上述定理的Corollary推论：

     令假设类含有k个假设，|H|=k，给定γ和δ，为了保证：

    

     至少在1-δ的概率下，满足条件：

     

 

3. 无限假设类情形

    根据Corollary推论，定义了为满足误差率所需的样本数目的界，与样本复杂度有关的结论。接下来要把它推广到无限假设类的情形。

    H以d个实数为参数，例如使用逻辑回归，解决包含n个特征的问题，d应该为n+1，所以逻辑回归会找到一个线性决策边界，以n+1个实数为参数。在计算机中用双精度浮点数64bit表示一个实数，那么此时用64d个位来表示参数，具有64d个状态，，为了满足这个条件，m符合：

   

    训练样本的数目大致和假设类的参数数目呈线性关系。这个论点并不是充分的，只是用来加深直观的理解。

 （1）分散的定义

    给定d个样本的集合S={x⁽¹⁾,...,x^(d)}，假设类H可以分散S，那么对于S的任意一种标记方式都可以从H中找到一个假设h能够对S的d个样本进行完美预测。

• H={二维上的线性分类器}

    

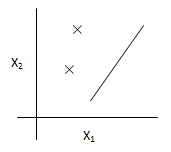
• H={三维上的线性分类器}

 

  （2）VC维

       给定一个假设类H，定义VC维（Vapnik-Chervonenkis dimension），记作VC(H)，表示能够被H分散最大集合的大小。如果一个假设类可以分散任意大的集合，那么它的VC维维无穷大。

       若H是所有二维线性分类器构成的假设类，VC(H)=3。即使也有几个特例例外，不过这并不影响整体。

   

       推广到一般情形，对于任意维度，线性分类器是n维的，也就是n维假设类对应的VC维度为n+1。

       定理：给定一个假设类H，令VC(H)=d，至少在1-δ的概率下，对于任意h∈H有如下结论：

      

       因此，至少在1-δ的概率下，以下结论也成立：

      

      第一个结论说明一般误差与训练误差之间的差异存在上界，由不等式右边的式子O()限定。第二个结论说明，若一般误差与训练误差相差不大的情况下，那么选择的假设的一般误差与最好的一般误差之间的差异最多是O()。

      Corollary：为了保证对于所有的h∈H有，也就是，至少在1-δ的概率下，要满足： 

      也就是为了保证一般误差与训练误差的差异足够小，假设类的VC维需要与m的阶相同。对于EMR来说，需要训练的样本数目大概和假设类的VC维呈线性关系，样本复杂度的上界由VC维给定，最坏的情况下，样本复杂度的上下界均由VC维确定。对于大多数合理的假设类，VC维总是与模型的参数成正比。而事实上，样本数目与模型参数数量也成线性关系。

      在SVM中，核函数将特征映射到无限维的特征空间，看似VC维度是无穷大的，因为它是n+1，而n为无穷大。事实证明：具有较大间隔的线性分类器假设类都有比较低的VC维。

      若，则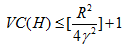

      仅包含较大间隔线性分类器假设类的VC维是有上界的，且上界并不依赖于x的维度。SVM会自动找到一个具有较小VC维的假设类，不会出现过拟合。

 

      最后，结合上述内容解释ERM与之前学习过的学习算法之间的联系。

     

 

      最理想的分类器是一个指示函数（阶梯函数），不是一个凸函数，事实证明线性分类器使训练误差最小是一个NP难问题。逻辑回归与支持向量机都可以看作是这个问题（ERM）的凸性近似。逻辑回归一般采用极大似然性，如果加入负号就可以得到图中的曲线，实际上是近似地在最小化训练误差，它是ERM的一种近似。同时，支持向量机也可以看作是ERM的一种近似，不同的是它尝试用两段不同的线性函数近似，看似是铰链的形状。