算法
1、排序算法 Sort
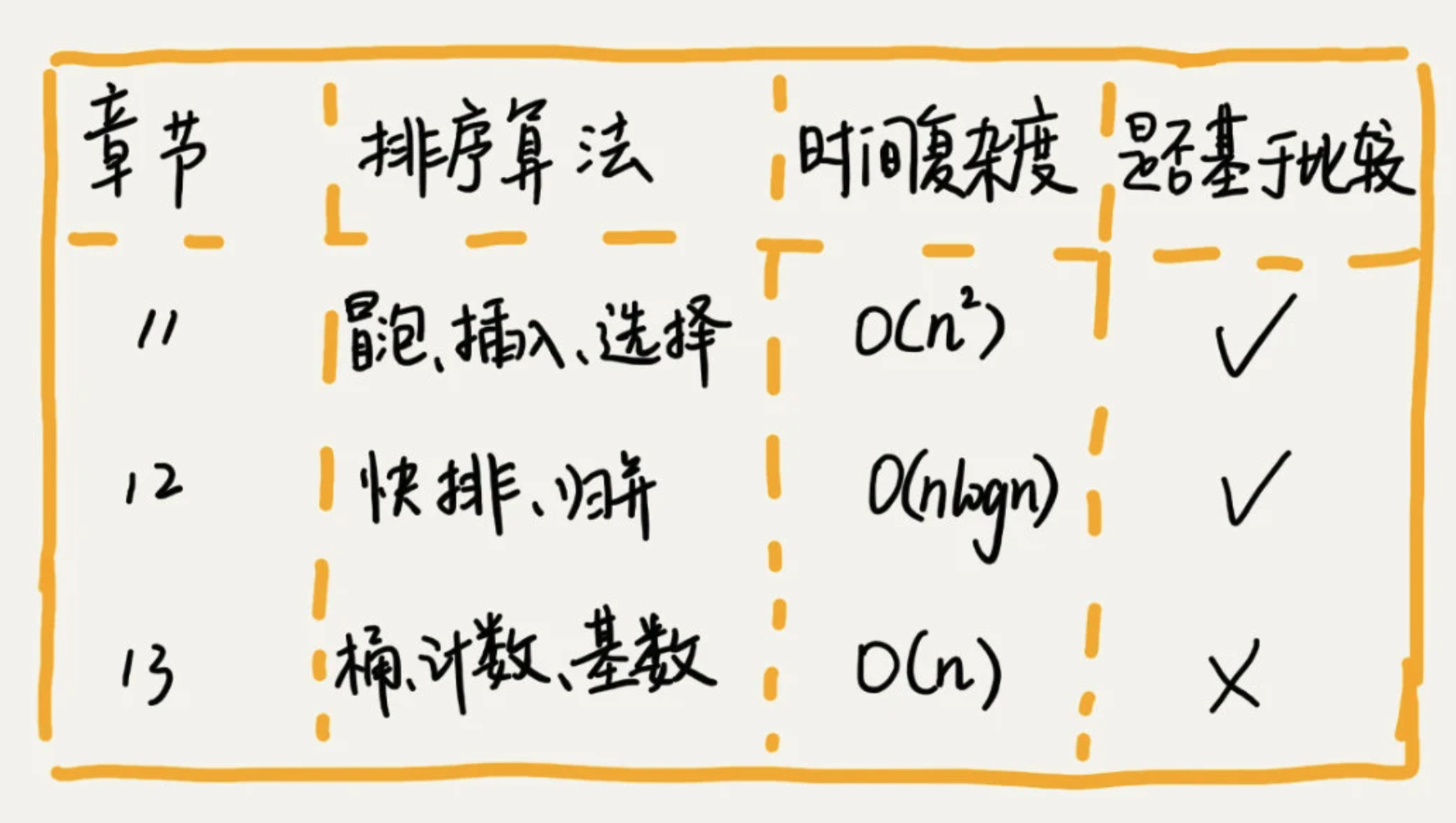1、排序算法的执行效率衡量指标
- 最好情况、最坏情况、平均时间复杂度
- 时间复杂度的系数、常数、低接
- 比较次数和交换次数
2、内存消耗
原地排序：除了存储数据本身的空间，不需要额外的辅助存储空间
3、稳定性
稳定的排序算法： 如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。
4、有序度：
数组中具有有序关系的元素对的个数
满有序度(完全有序的数组)： n*(n-1)/2
逆序度 = 满有序度 - 有序度
1、冒泡排序 Bubble Sort
每次挨个对比相邻的两个元素，如果比后面的大，则交换位置。重复n次，排序完成。
这个是正常情况下的冒泡次数，当某次冒泡没有数据交换时，说明已经完全有序，后面的冒泡操作可以不用继续。
def bubble_sort(alist):
if len(alist) <= 1:
return
for i in range(0, len(alist)-1):
flag = False
for j in range(0, len(alist)-1-i):
if alist[j] < alist[j+1]:
alist[j], alist[j+1] = alist[j+1], alist[j]
flag = True
# 如果当前冒泡已经达到满排序，直接退出
if flag == False:
break
- 原地排序算法：空间复杂度为O(1)
- 稳定排序算法：相邻两个元素相等时，不交换
- 时间复杂度：最好O(n)、最坏O(n²)、平均O(n²)
2、插入排序 Insertion Sort
将数组分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。然后 取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间的数据一直有序，重复这个过程，知道未排序区间中元素为空。
def insert_sort(alist):
if len(alist) <= 1:
return
for i in range(1, len(alist)):
# 对未排序区进行排序
for j in range(i, 0, -1):
if alist[j] > alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
else:
break
- 原地排序算法：空间复杂度为O(1)
- 稳定排序算法：对于值相等的元素，未排序区出现的，插入到已排序区元素的后面，即位置不变
- 时间复杂度：最好O(n)、最坏O(n²)、平均O(n)
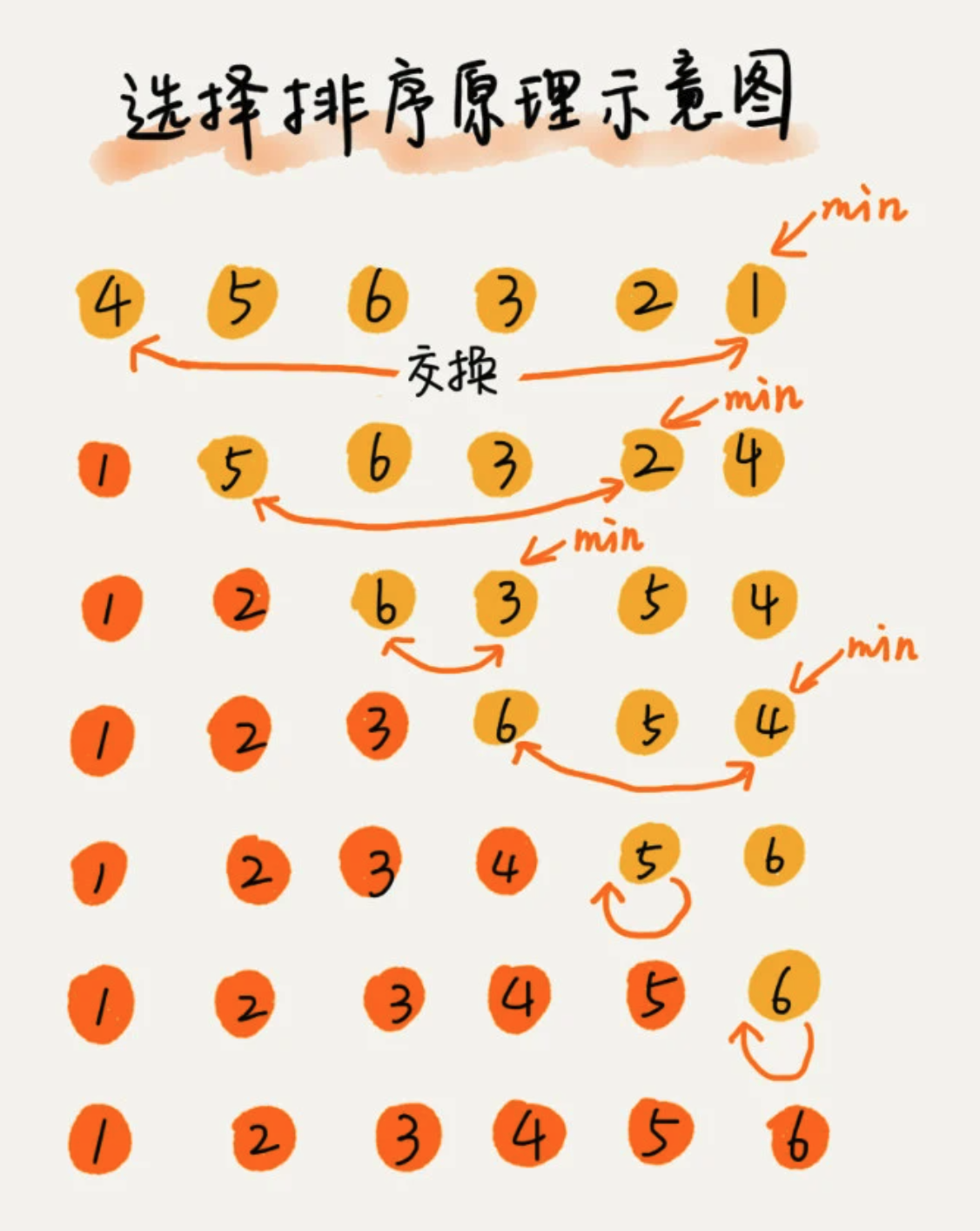
3、选择排序 Selection Sort
该排序算法，也分已排序区间和未排序区间。但选择排序每次会从未排序区间中找到最小元素，将其放在已排序区间的末尾。
def select_sort(alist):
if len(alist) <= 1:
return
for i in range(0, len(alist)-1):
min_index = i
for j in range(i+1, len(alist)):
if alist[j] < alist[min_index]:
min_index = j
alist[i], alist[min_index] = alist[min_index], alist[i]
- 原地排序算法：空间复杂度为O(1)
- 不稳定排序算法：每次获取到最小元素，都需要和已排序区的最小元素位置发生互换
- 时间复杂度：最好O(n²)、最坏O(n²)、平均O(n²)
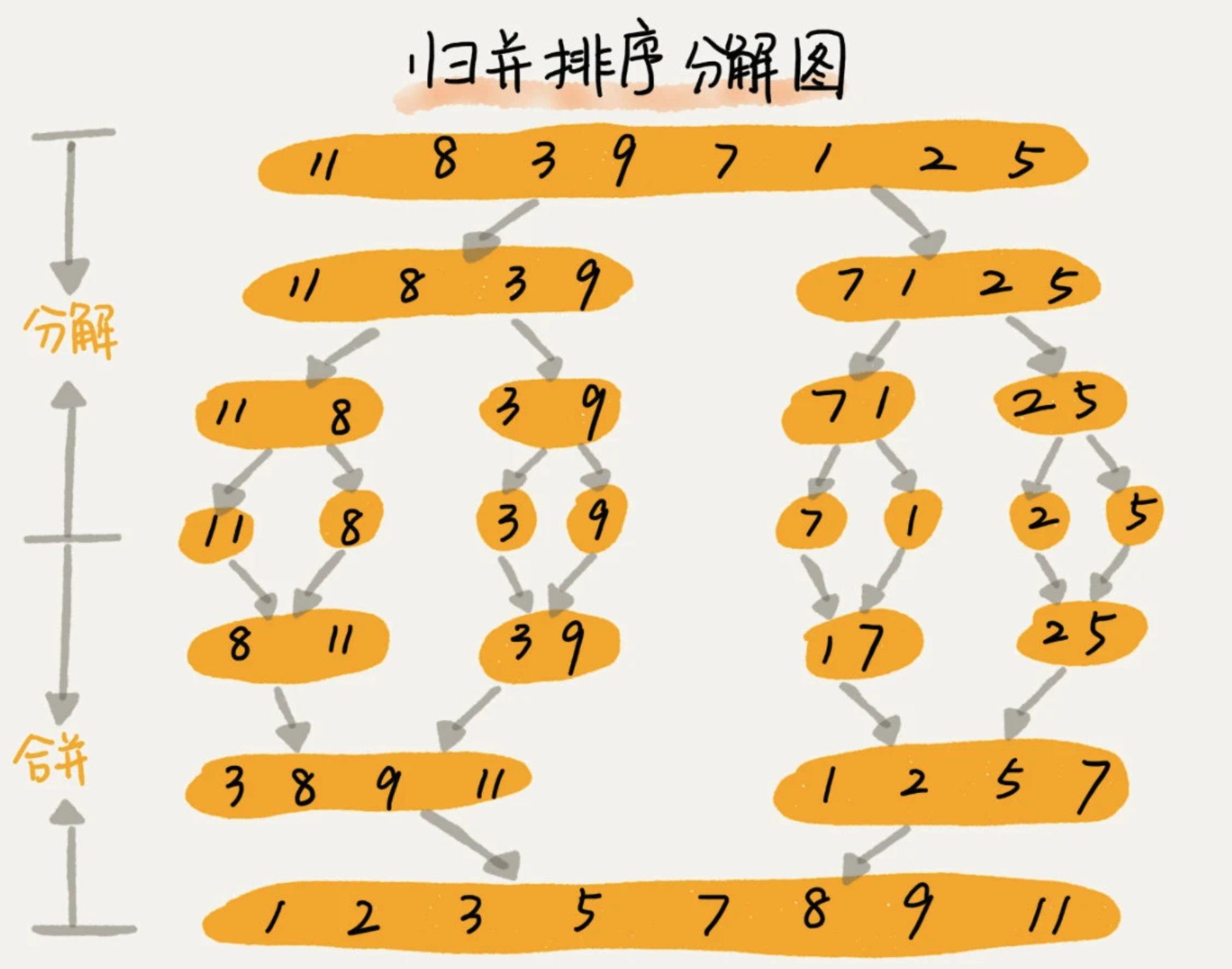
4、归并排序 Merge Sort
针对一个数组，将数组从中间分成前后两部分，然后对前后两部分进行分别排序，再将排序好的两部分合并在一起。
def merge_sort(alist):
n = len(alist)
# 递归终止条件
if n <= 1:
return alist
mid = n // 2
left_li = merge_sort(alist[:mid])
right_li = merge_sort(alist[mid:])
result = []
left_pointer, right_pointer = 0, 0
while left_pointer < len(left_li) and right_pointer < len(right_li):
if left_li[left_pointer] < right_li[right_pointer]:
result.append(left_li[left_pointer])
left_pointer += 1
else:
result.append(right_li[right_pointer])
right_pointer += 1
result += left_li[left_pointer:]
result += right_li[right_pointer:]
return result
- 原地排序算法：空间复杂度为O(n)
- 稳定排序算法：值相等的元素，不交换位置
- 时间复杂度：最好O(nlogn)、最坏O(nlogn)、平均O(nlogn)
5、快速排序 Quick Sort
如果要排序数组中下标从 p 到 r 之间的一组数据，选择 p 到 r 之间的任一个数据作为pivot(分区点)。遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放在中间。
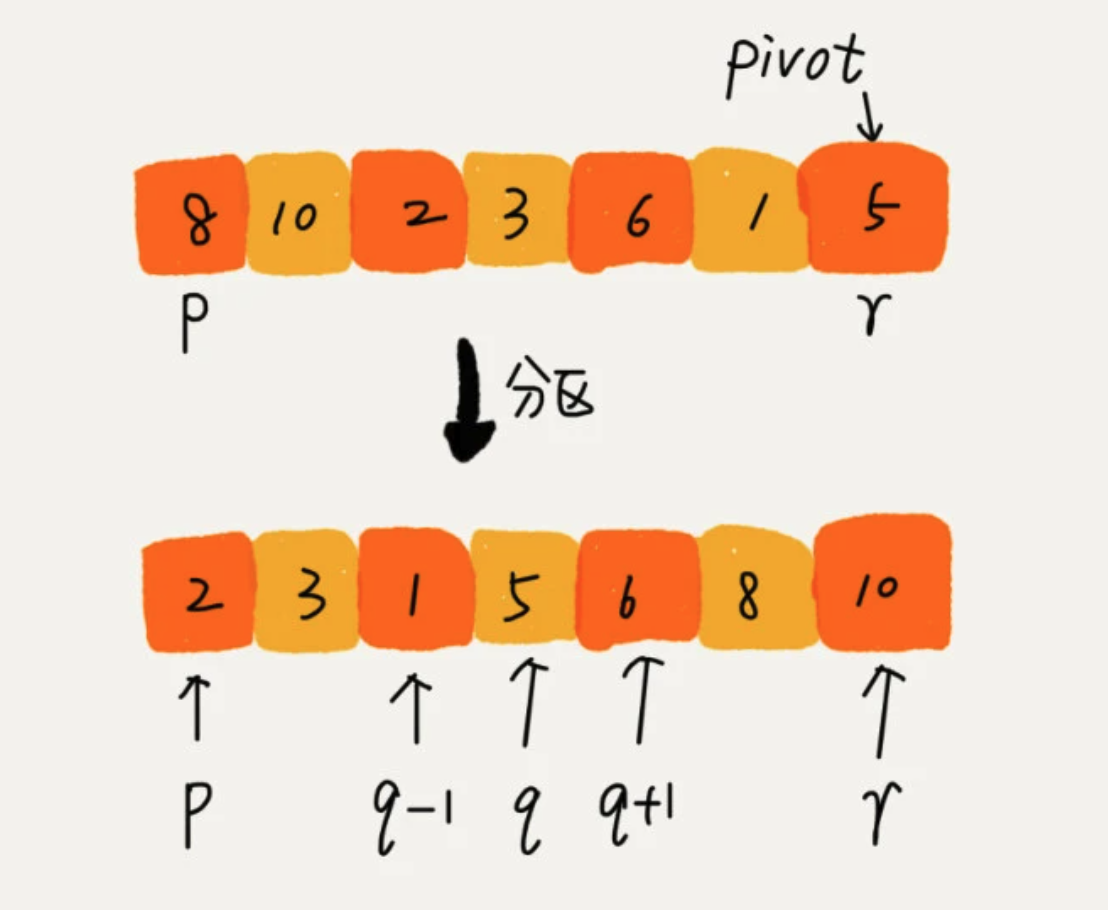
然后根据分治、递归的思想，分别处理两边的数据。
def quick_sort(alist, start, end):
if start > end:
return
pivot = alist[end]
low = start
high = end
# 小于pivot 放在左边，大于pivot放在右边
while low < high:
while low < high and alist[low] <= pivot:
low += 1
alist[high] = alist[low]
while low < high and alist[high] > pivot:
high -= 1
alist[low] = alist[high]
alist[low] = pivot
quick_sort(alist, low+1, end)
quick_sort(alist, start, high-1)
- 原地排序算法：空间复杂度为O(1)
- 不稳定排序算法
- 时间复杂度：最好O(nlogn)、最坏O(n2)、平均O(nlogn)
6、桶排序 Bucket Sort
将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。
理想情况下，时间复杂度：O(n)
7、计数排序 Counting Sort
其属于桶排序的一种特殊情况。当要排序的n个数据，所处的范围并不大的时候，比如最大值是k，我们可以把数据分为k个桶，每个桶内的数据值都是相同的，省掉了桶内排序的时间。
从计数的来看，举一个例子
假设只有 8 个考生，分数在 0 到 5 分之间。这 8 个考生的成绩我们放在一个数组 A[8]中，它们分别是：2，5，3，0，2，3，0，3。考生的成绩从 0 到 5 分，我们使用大小为 6 的数组 C[6]表示桶，其中下标对应分数。不过，C[6]内存储的并不是考生，而是对应的考生个数。
代码实现：
import itertools
def counting_sort(alist):
if len(alist) <= 1:
return
# a中有counts[i]个数不大于i
counts = [0] * (max*(alist) + 1)
for num in alist:
counts[num] += 1
counts = list(intertools.accumulate(counts))
# 临时数组，存储排序之后的结果
a_sorted = [0] * len(alist)
for num in reversed(alist):
index = counts[num] - 1
a_sorted[index] = num
counts[num] -= 1
alist[:] = a_sorted
8、基数排序 Radix Sort
从末尾依次按照单个元素排序，直到头部元素，即可排序完成。需要每一个元素的排序算法是稳定的，如果位数不够，可以补"0"
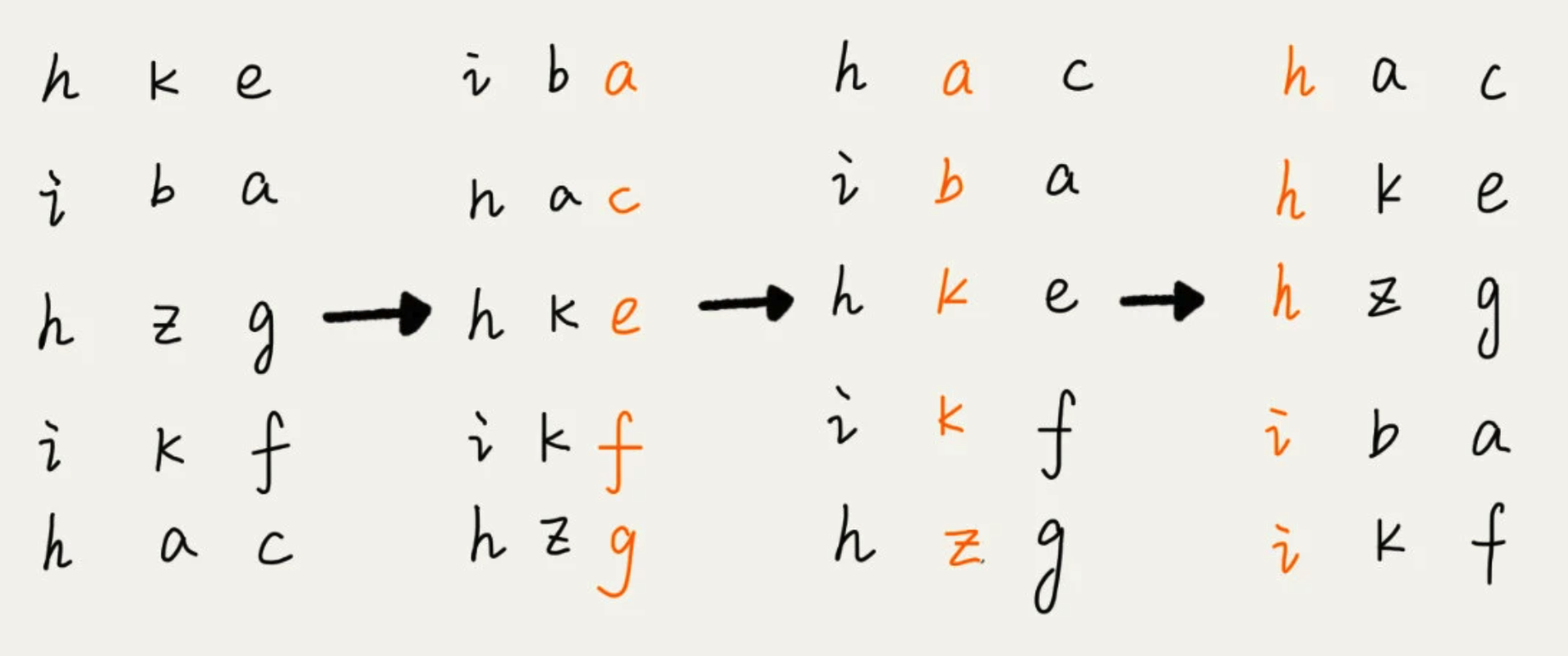
9、堆排序 Heap Sort
时间复杂度稳定的 O(nlogn)
堆排序过程大致分为两个步骤：建堆和排序
1、建堆
建堆的是时间复杂度是 O(n)
有两种思路
第一种，在堆中插入元素。尽管数组中包含n个数据，但可以假设，起初堆中只包含一个数据，就是下标为 1 的数据。然后，调用插入操作，将下标从 2 到 n 的数据依次插入到堆中，这样就将包含n个数据的数组，组成了堆。也就是从前往后处理数据，每个数据插入的收，从下往上堆化。
第二种，将已经存在n个数据的数组，从后往前处理数组，每个数据从上往下堆化。
2、排序
建堆完成后，得到一个大顶堆。数组的第一个元素就是堆顶，也就是最大的元素。将它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。以此类推，直到堆中剩下下标为 1的元素，排序完成。
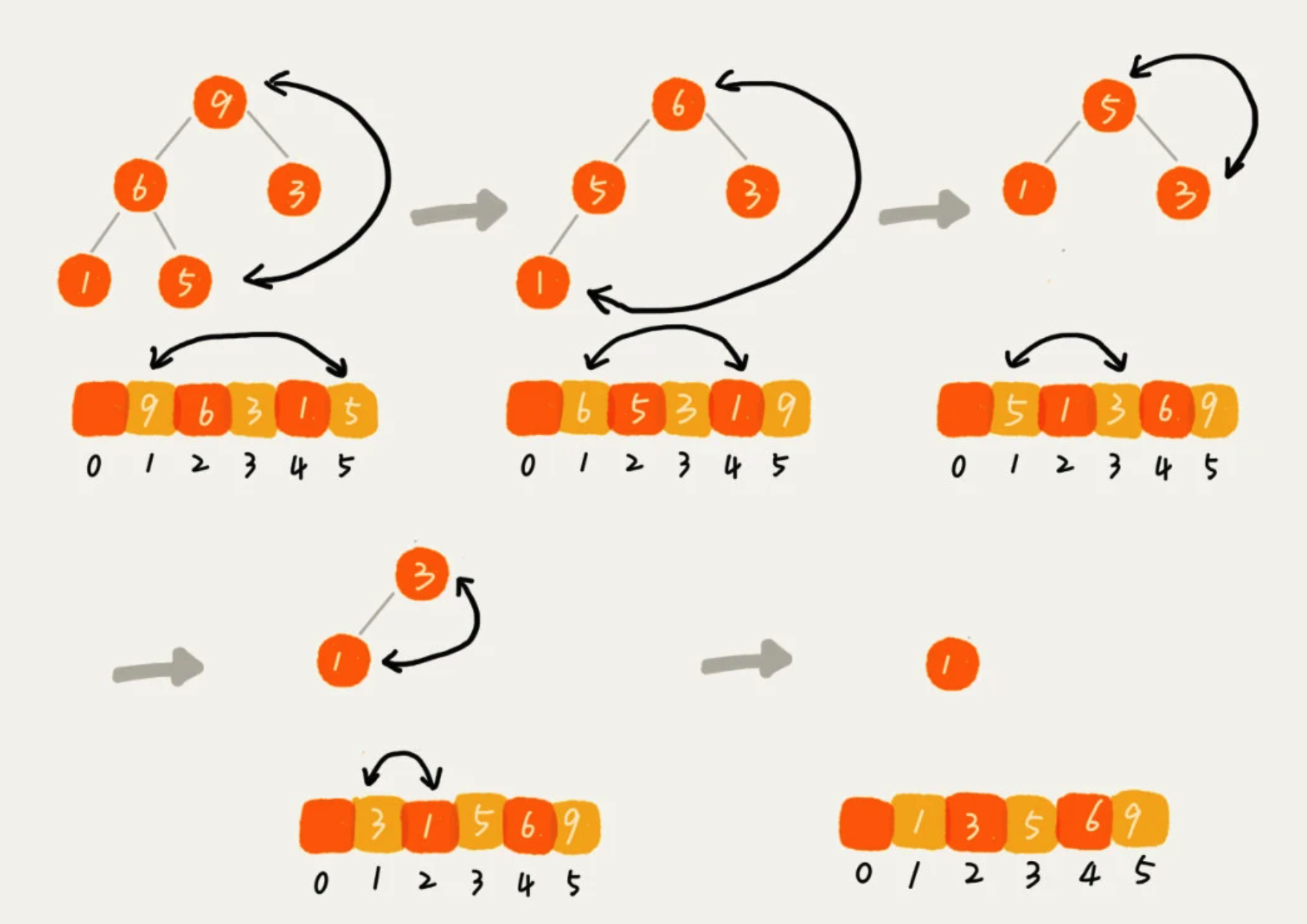
排序的时间复杂度是 O(logn)
所以，堆排序的总时间复杂度为 O(nlogn)。
4、应用
1、优先队列
从优先级队列取出优先级最高的元素，就相当于取出 堆顶元素。其实际应用如：
1、合并有序小文件
假设有100个小文件，每个文件的大小是100MB，每个文件中存储的都是有序的字符串。希望将这些100个小文件合并成一个有序的大文件。
解决：
从小文件中取出的字符串放入到小顶堆中，也堆顶元素，也就是优先级队列队首的位置，就是最小的字符串。然后将这个字符串放入到大文件中，并将其从堆顶删除。然后从小文件中取出下一个字符串，循环这个过程。
2、定时器
假设定时器维护了多个定时任务，每个任务出发都有一个时间点。定时器每过一个很小的时间，就扫描一边任务，看是否有任务到达设定的执行之间，如果有，就拿出来执行。
解决：
按照任务的设定执行时间，将这些任务存储在优先队列中，队列首部（也就是小顶堆的堆顶）存储的是最先执行的任务。
这样每过那个很小的定时时间后，就不用扫描整个任务了，直接取出堆顶的任务，执行即可。堆内再进行堆化。
2、利用堆求 Top K
- 针对静态数据，数据集合已经固定
维护一个大小为 K 的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。如果比堆顶元素大，就把堆顶元素删除，将这个元素插入到堆中；如果比堆顶元素小，则不处理，直到遍历完数组。堆中就是前 K 大数据。
遍历数组需要 O(n)，堆化需要 O(log K)，所以时间复杂度为 O(nlog k)
- 针对动态数据
维护一个 K 大小的小顶堆，当有数据被添加到集合中时，跟堆顶元素对比，如果比堆顶元素大，就把堆顶元素删除，将这个元素插入到堆中；如果比堆顶元素小，则不处理。这样，始终保持 有一个 大小为 K 的小顶堆，可以查询前 K 大数据。
3、求中位数
维护两个堆，一个大顶堆，一个小顶堆。大顶堆中存储牵绊部分数据，小顶堆存储后半部分数据，且小顶堆中的数据都大于大顶堆中的数据。
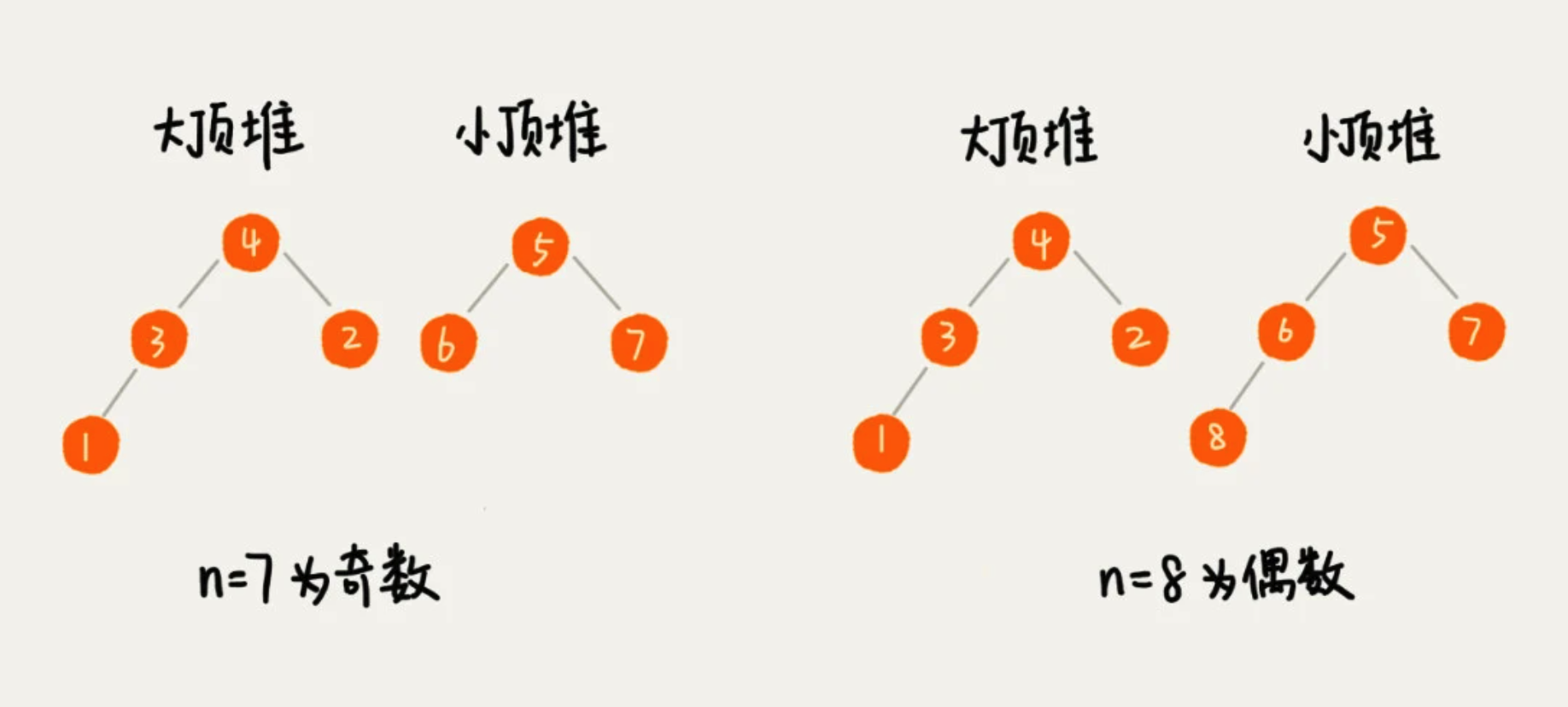
当数据插入导致，出现 大顶堆的元素 多余 小顶堆的时候，就将大顶堆的堆顶，不停的移动到小顶堆中。
插入数据，导致需要堆化，所以时间复杂度为 O(logn)，中位数，就是大顶堆的堆顶元素。O(1)
2、二分查找 Bsearch
针对一个有序的数据集合，查找思想类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为0。
优势：时间复杂度 (logn)
劣势：局限性（依赖顺序表结构、有序数据、针对较大数据量）
1、简单实现
def bsearch(alist, target):
low, high = 0, len(alist) - 1
while low <= high:
# 防止值溢出
mid = low + (high - low) // 2
if alist[mid] == target:
return mid
elif alist[mid] < target:
low = mid + 1
else:
high = mid - 1
return -1
2、递归实现
def bsearch_internally(alist, low, high, target):
if low > high:
return -1
# 将整除2，转换为 位运算
mid = low + int((high-low) >> 1)
if alist[mid] = traget:
return mid
elif alist[mid] < target:
return bsearch_internally(alist, mid+1, high, target)
else:
return bsearch_internally(alist, mid-1, high, target)
bsearch_internally(alist, 0, len(alist)-1, target)
3、有序集合中存在重复数据，查找第一个值等于给定值
def bsearch(alist, target):
low, high = 0, len(alist) - 1
while low <= high:
mid = low + int((high - low) >> 1)
if alist[mid] < target:
low = mid + 1
else:
high = mid - 1
# 当游标 小于 数组长度 并且 ，最小的游标等于 目标值
if low < len(alist) and alist[low] == target:
return low
else:
return -1
4、有序集合中存在重复数据，查找最后一个值等于给定值
def bsearch(alist, target):
low, high = 0, len(alist) - 1
while low <= high:
mid = low + int((high - low) >> 1)
if alist[mid] < target:
low = mid + 1
else:
high = mid - 1
# 当游标 大于0 并且 ，最大的游标等于 目标值
if high > 0 and alist[high] = target:
return high
else:
return -1
3、哈希算法 Hash
将任意长度的二进制值串映射为固定长度的二进制值串，这个映射的规则就是哈希算法，通过原始数据映射之后得到的二进制值串就是哈希值。
其在实际中有常见的易用场景：
1、安全加密
最常用于加密的哈希算法是 MD5(MD5 Message-Digest Algorithm，MD5消息摘要算法)和SHA(Secure Hash Algorithm，安全散列算法)。
以及 DES(Data Encryption Standard，数据加密标准)、AES(Advanced Encryption Standard，高级加密标准)。
- 散列冲突的概率要很小
鸽巢原理：如果有 10 个鸽巢，有 11 只鸽子，那肯定有 1 个鸽巢中的鸽子数量多于 1 个，换句话说就是，肯定有 2 只鸽子在 1 个鸽巢内。
因此用MD5的例子，哈希值是固定的128位二进制串，最多能表示2^128个数据，就必然会存在哈希值相同的情况。
2、唯一标识
针对图片来讲，可以从图片的二进制码串开头取100字节，从中间取100个字节，从最后再取100字节，将这300字节放到一块，通过哈希算法（如MD5），得到一个哈希字符串，用它作为图片的唯一标识。以此来更高效地判断图片是否在图库中。
进一步提高效率，可以将每一张图片的唯一标识，和相应的图片文件的路径信息，都存储在散列表中。当要查看某个图片是否在图库中时，先通过哈希算法对图片取唯一标识，然后在散列表中查找是否存在这个唯一标识。
如果不存在，则说明图片不再图库中；如果存在，通过散列表获取到文件路径，获取已经存在的图片，进行全量比对，看是否完全一样。
3、数据校验
BT 下载的原理是基于 P2P 协议的。我们从多个机器上并行下载一个 2GB 的电影，这个电影文件可能会被分割成很多文件块（比如可以分成 100 块，每块大约 20MB）。等所有的文件块都下载完成之后，再组装成一个完整的电影文件就行了。
通过哈希算法，对 100 个文件块分别取哈希值，并且保存在种子文件中。哈希算法有一个特点，对数据很敏感。只要文件块的内容有一丁点儿的改变，最后计算出的哈希值就会完全不同。所以，当文件块下载完成之后，我们可以通过相同的哈希算法，对下载好的文件块逐一求哈希值，然后跟种子文件中保存的哈希值比对。如果不同，说明这个文件块不完整或者被篡改了，需要再重新从其他宿主机器上下载这个文件块。
4、散列函数
简单、追求效率
5、负载均衡
实现一个会话粘滞（session sticky）的负载均衡算法：
通过哈希算法，对客户端IP地址或会话ID计算哈希值，将取得的哈希值与服务器列表的大小进行取模运算，最终得到的值就是应该被路由到的服务器编号。
6、数据分片
针对较大数据，在哈希计算中，整体会比较耗时，这个时候可以将数据进行分片，在不同的机器分别进行哈希计算哈希值，最终再构建整体的散列表。
7、分布式存储
如分布式缓存，针对海量数据，西安通过哈希算法对数据取哈希值，然后对机器个数取模，这个最终值就是应该存储的缓存机器编号。
当需要扩容的时候，所有数据需要重新计算哈希值，原有的哈希值失效，可能会导致雪崩效应。
解耦，增加一个中间层，使得哈希函数以来一个稳定的区间数（2^32），当服务器数量变化时，若增加，则搬移部分数据，若减少，同样重新分配缓存数据 这样只会有部分缓存被影响。
4、优先搜索 First Search
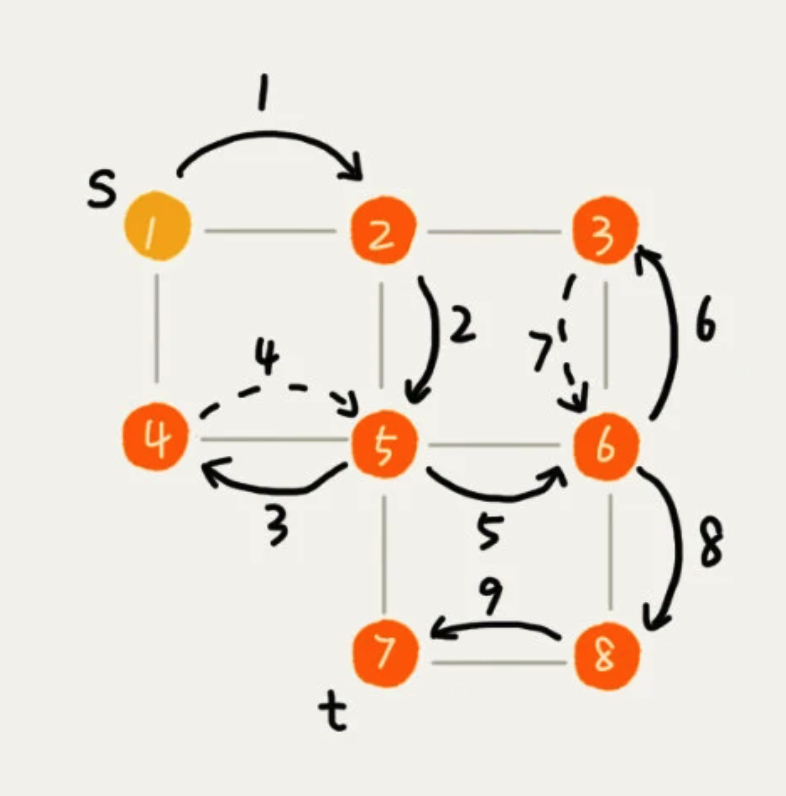
1、广度优先搜索 BFS Breadth-First-Search
一种“地毯式”层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近的，依次往外搜搜。
2、深度优先搜索 DFS Depth-First-Search
采用了 回溯思想，从一条路径一直走到头，然后返回到上一个分叉路口，再进入另一条路径，直到没有顶点。
from collections import deque
class Graph():
# s是开始顶点，t是要搜索到的目标顶点
def __init__(self, num_vertices)
# 图的度的数量
self._num_vertices = num_vertices
# 用二维数组来保存图
self._adjacency = [[] for _ in range(num_vertices)]
# 添加度
def add_edge(self, s, t):
self._adjacency[s].append(t)
self._adjacency[t].append(s)
def _generate_path(self, s, t, prev):
# prev来记录搜索路径
if prev[t] or s != t:
yield from self._generate_path(s, prev[t], prev)
yield str(t)
def bfs(s, t):
if s == t: return
# 用来记录已经访问的节点
visited = [False] * self._num_vertices
visited[s] = True
# 双端队列，存储已经被访问、但相连的顶点还没有被访问的顶点
q = deque()
q.append(s)
prev = [None] * self._num_vertices
while q:
# 左侧弹出一个元素(List)，即第一层
v = q.popleft()
# 遍历这个元素内部
for neighbour in self._adjacency[v]:
# 如果没有访问过的
if not visited[neighbour]:
# 将这个 list元素，赋值给 prev记录
prev[neighbour] = v
# 如果内部元素 是目标元素，直接打印
if neighbour == t:
print('-->'.join(self._generate_path(s, t, prev)))
return
# 检查完了之后，记录该顶点已经访问
visited[neighbour] = True
# 添加到队列中
q.append(neighbour)
def dfs(self, s, t):
# 用来标识，找到顶点t之后，不再递归
found = False
visited = [False] * self._num_vertices
prev = [None] * self._num_vertices
def _dfs(from_vertex):
nonlocal found
if found: return
visited[from_vertex] = True
if from_vertex == t:
found = True
return
for neighbour in self._adjacency[from_vertex]:
if not visited[neighbour]:
prev[neighbour] = from_vertex
_dfs(neighbour)
_dfs(s)
print("->".join(self._generate_path(s, t, prev)))
if __name__ == "__main__":
graph = Graph(8)
graph.add_edge(0, 1)
graph.add_edge(0, 3)
graph.add_edge(1, 2)
graph.add_edge(1, 4)
graph.add_edge(2, 5)
graph.add_edge(3, 4)
graph.add_edge(4, 5)
graph.add_edge(4, 6)
graph.add_edge(5, 7)
graph.add_edge(6, 7)
graph.bfs(0, 7)
graph.dfs(0, 7)
5、字符串匹配算法
1、BF算法 Brute Force
即暴力匹配算法，也叫朴素匹配算法。
在字符串A中查找字符串B，那么字符串A就是主串，字符串B就是模式串。
该算法思想就是：在珠串中，检查起始位置分别是：0、1、2……n-m 且长度为 m 的 n-m+1 个子串。因此时间复杂度为 O(n*m)
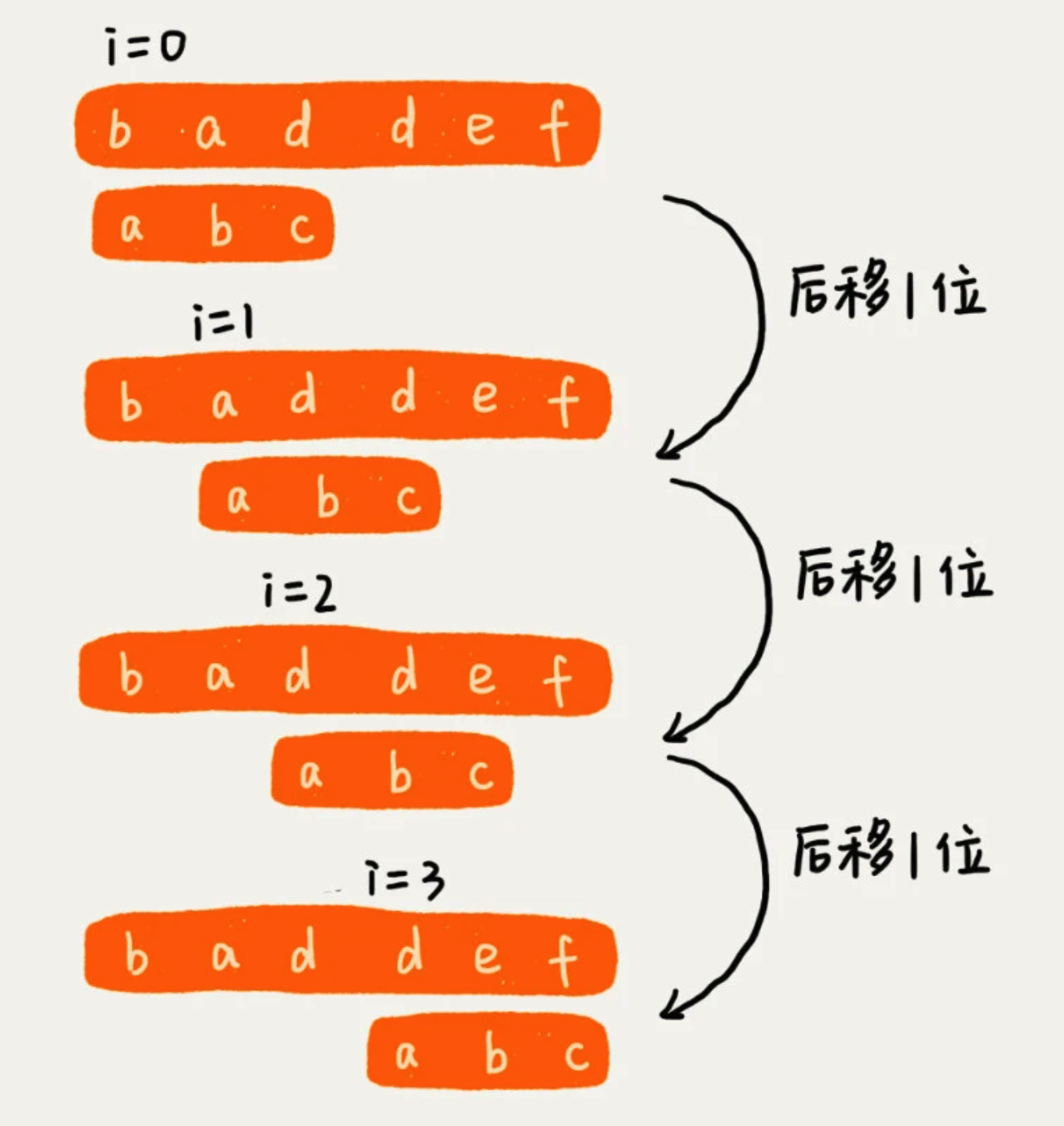
优点：
- 实际开发中，模式串和主串不会太长，且匹配到的时候，就会直接停止，效率会相对较高。
- 思想简单，代码实现简单，不容易出错。
2、RK算法 Rabin-Karp
其思想是：通过哈希算法对主串中 n-m+1 个子串分别求哈希值，然后逐个与模式串的哈希值比较。这里重点在于哈希算法的实现，不然会很容易造成哈希冲突。
假设要匹配的字符串集中只包含K个字符串，可以用一个K进制数来表示一个子串，这个 K 进制转化为十进制数，作为子串的哈希值。
哈希算法
比如要处理的字符串中只包含 a~z 这26个小写字母，就用二十六进制来表示一个字符串。将这26个字符映射到 0~25 这 26 个数字，a就是0，b就是1，以此类推。
在十进制的表示法中，一个数字的值是通过下面方式算出来的。对应到二十六进制，一个把包含 a到z这26个字符的字符串，计算哈希的时候，只需要把进位 10 改为 26.
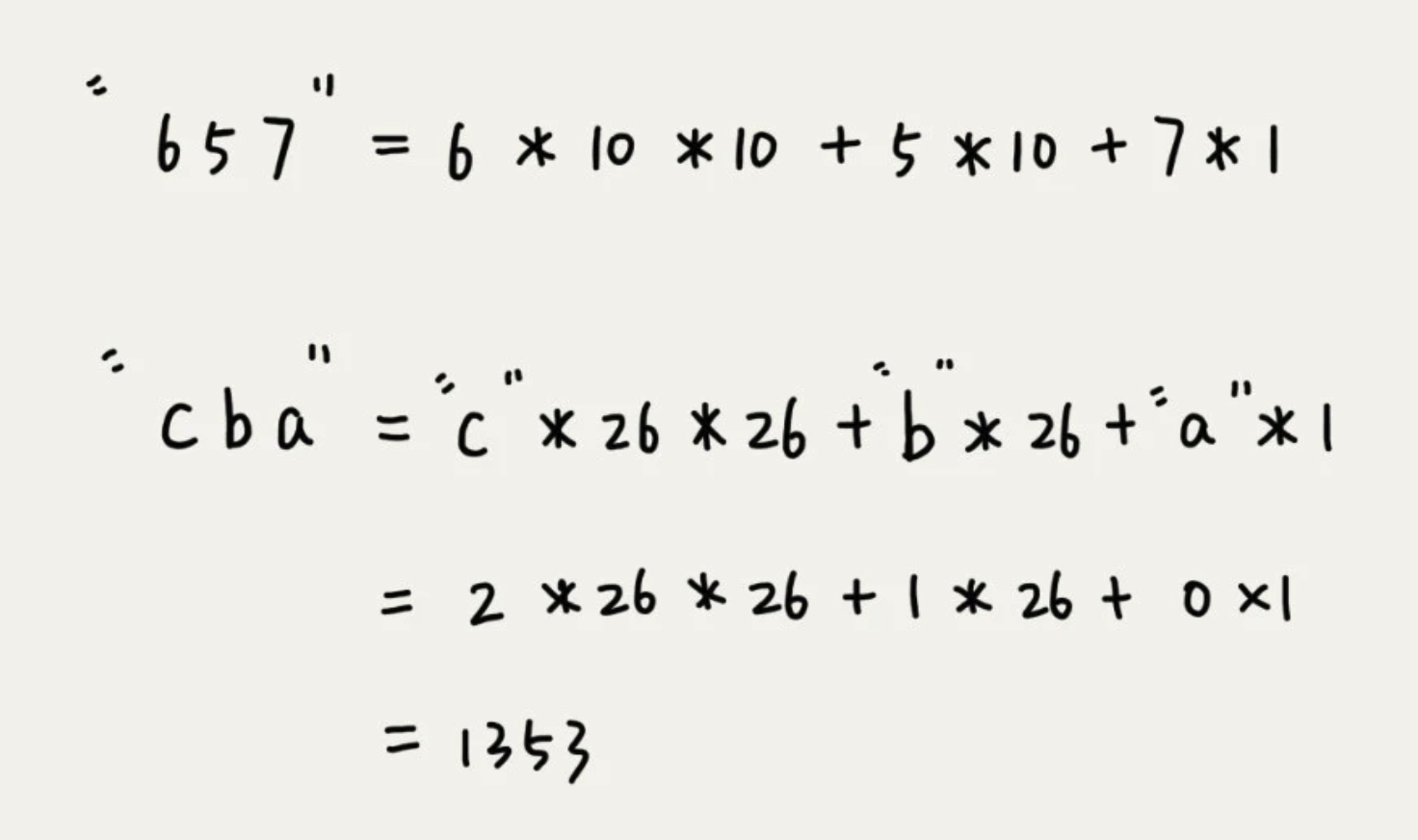
这种哈希算法有一个特点，在主串中，相邻两个子串的哈希值的计算公式有一定关系。也就是，后一个是前一个 * 26的值。
计算每个子串的哈希值，需要扫描一遍主串，这部分时间复杂度是 O(n)，
模式串的哈希值与每个子串的哈希值进行比较的时间复杂度是O(1)，总共比较 n-m+1 个子串，这部分是时间复杂度是 O(n)。
所以整体时间复杂度是 O(n)
3、BM算法 Boyer-Moore
当模式串和主串某个字符不匹配的时候，能够跳过一些肯定不会匹配的情况，将模式串往后多滑动几位。
1、坏字符规则
从模式串的末尾往前倒着匹配，当发现某个字符没法匹配的时候，把这个没有匹配的字符叫做坏字符（主串中的字符）。
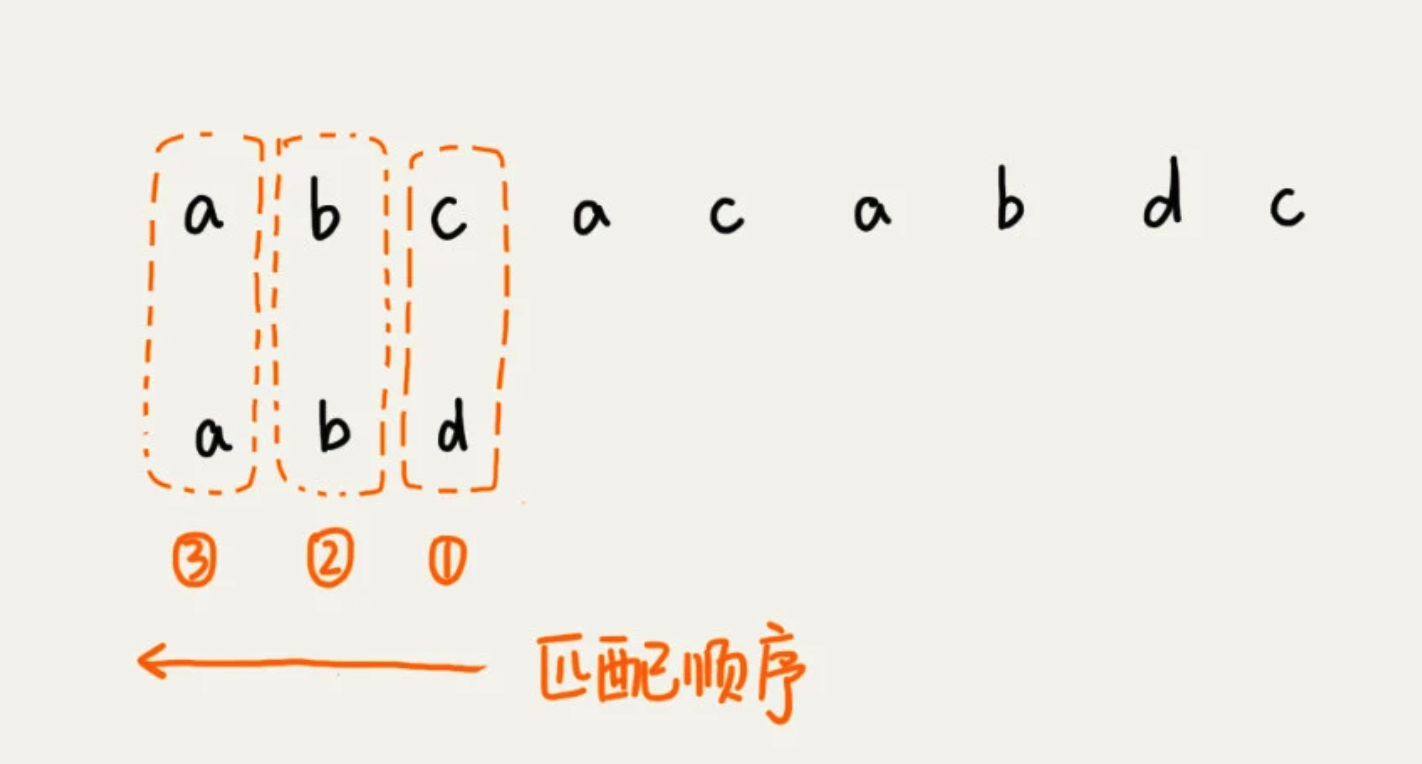
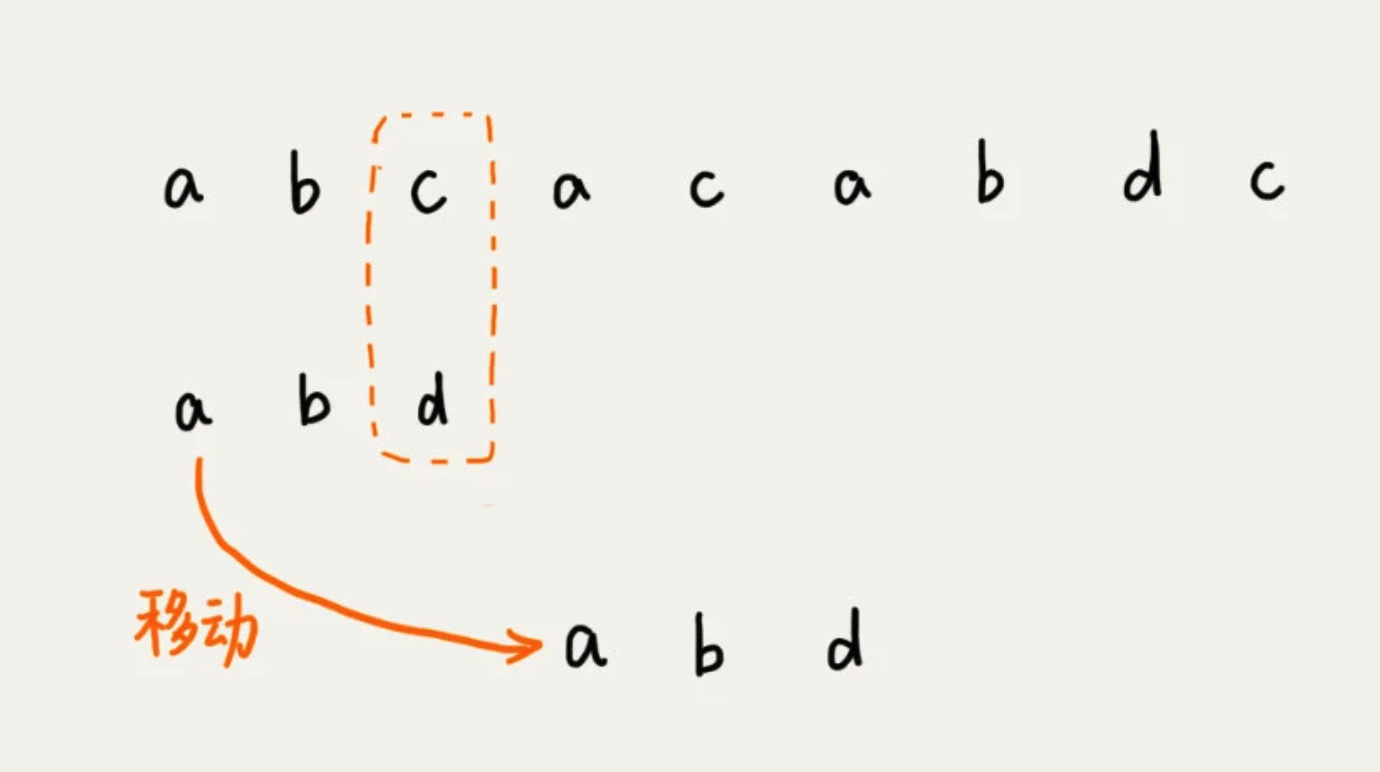
拿着字符 c 在模式串中查找，发现模式串中不存在这个字符。这时，直接将模式串往后滑动三位，再开始比较。
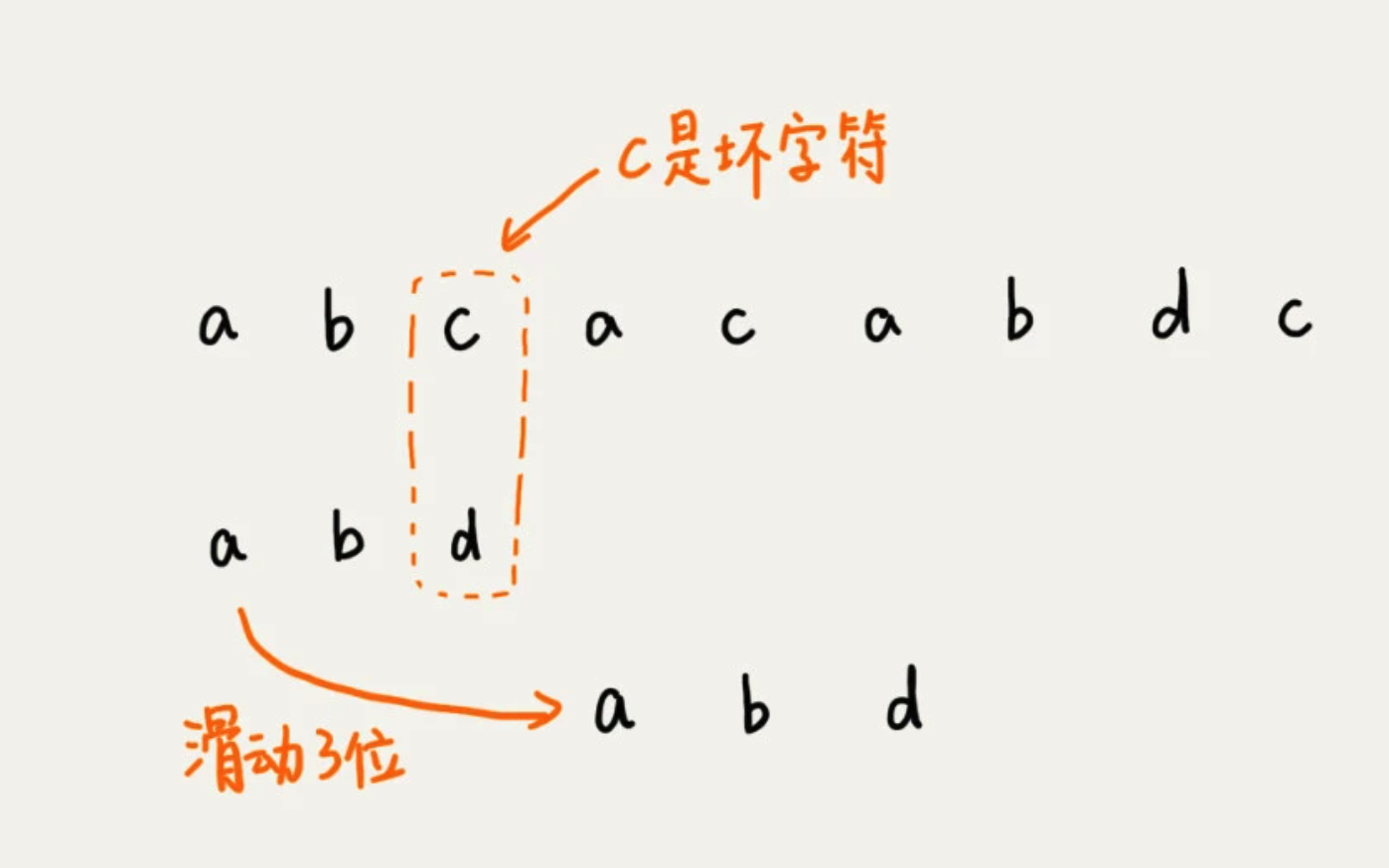
这时，发现模式串中最后一个字符 d ，还是无法跟，主串中的 a 匹配。这时，注意字符 a 在模式串中是存在的，就需要将模式串往后滑动两位，让两个 a 上下对齐。
当发生不匹配的时候，将坏字符对应的模式串中的字符下标记为 si。如果坏字符在模式串中存在，就将坏字符在模式串中的下标记为 xi。如果不存在，把 xi 记作 -1.那模式串往后移动的位数就等于 si - xi。
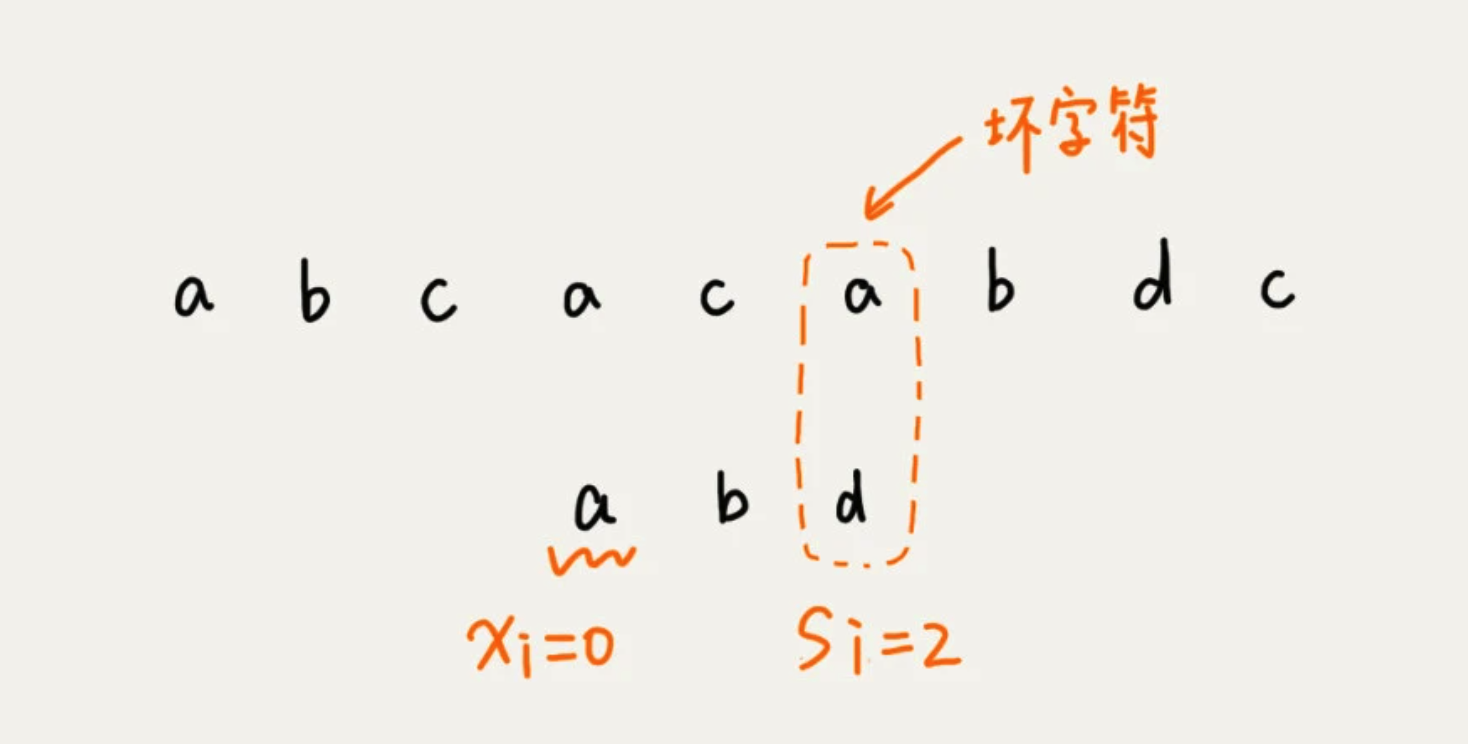
如果，坏字符串在模式串中多处出现，为了滑动过多，选择最靠后的那个。
然而，因为不存在时记作 -1，如主串是 aaaaaaaaaaaaaaaa，模式串是 baaa，那么就会导致相减之后，出现负数的情况。因此，还需要好后缀规则。
2、好后缀规则
将已经匹配的 bc 叫做 好后缀，记作 {u}。拿它在模式串中查找，如果找到了另一个跟 {u} 想匹配的子串 {u*}，那么就将模式串滑动到子串{u*}与主串中{u}对齐的位置。
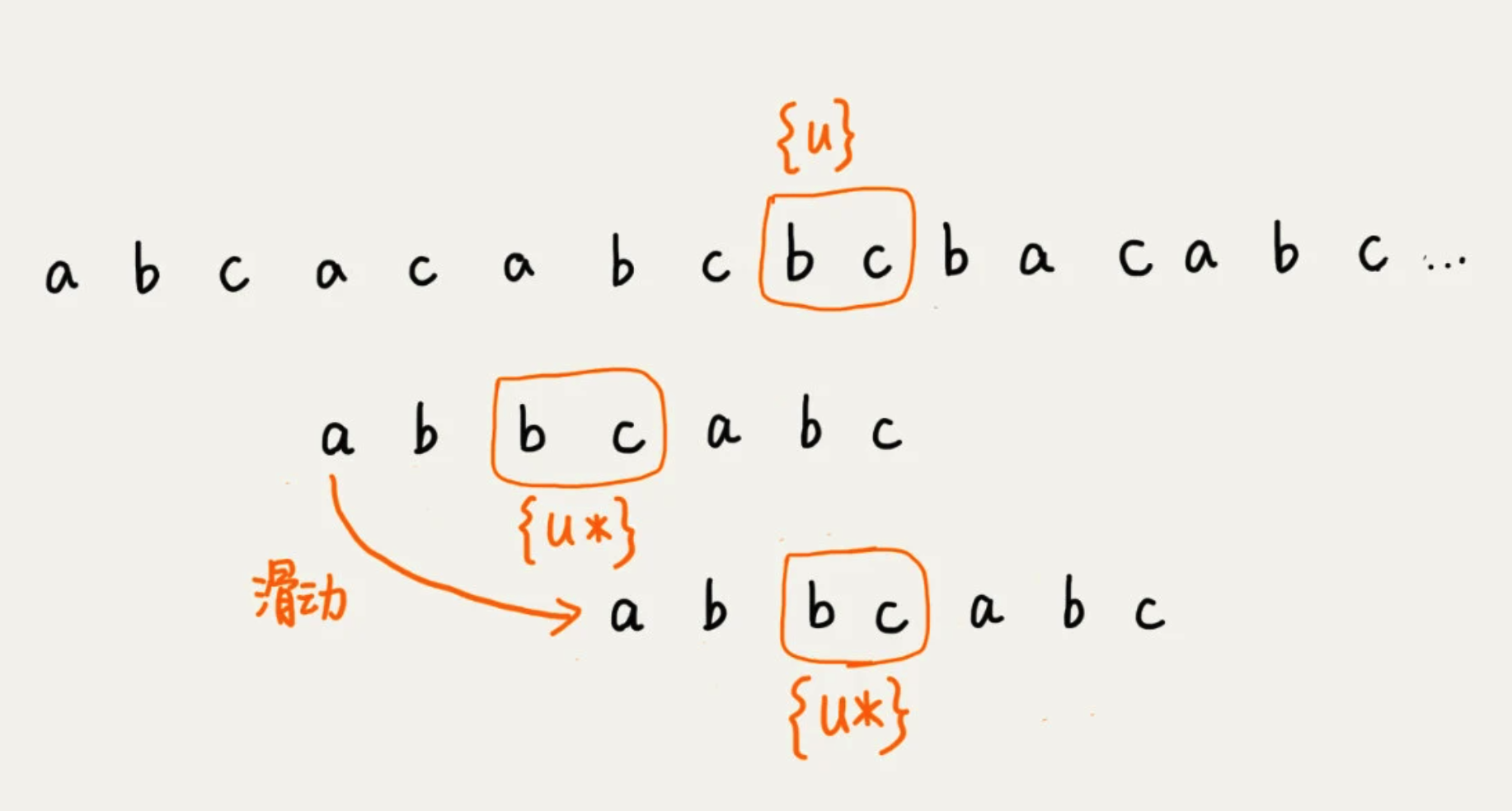
如果找不到的话，就直接划到主串{u}的后面，会导致过度滑动。正确应该是，滑动到主串{u}的最后一个字符下面。
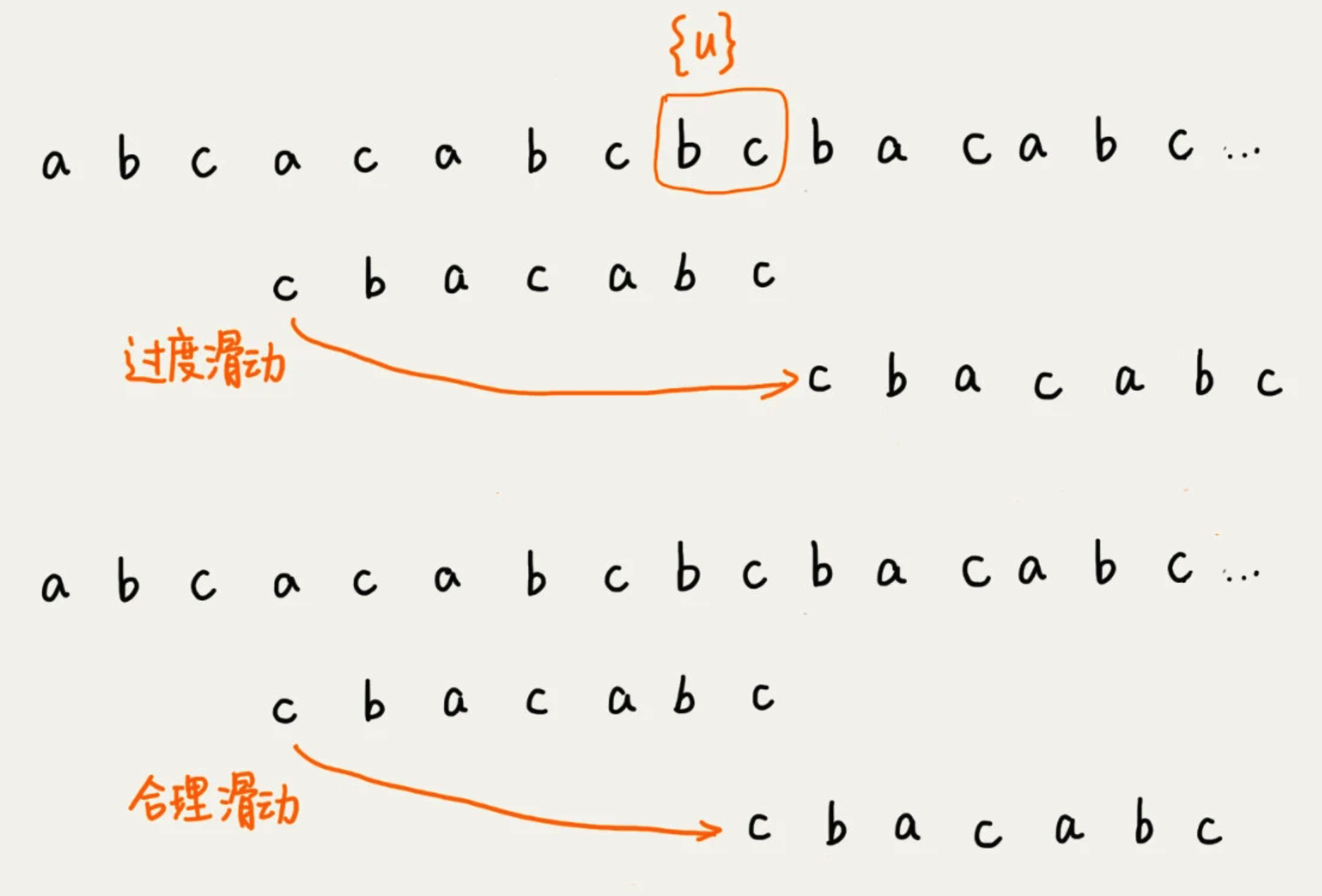
在滑动过程中，会导致以下两个情况。
规则选择：
分别计算好后缀和坏字符往后滑动的位数，然后取两个数中最大的，作为模式串往后滑动的位数，可以避免坏字符串规则的，滑动位数为负的情况。
3、实现
SIZE = 256
def bm(main, pattern):
assert type(main) is str and type(pattern) is str
n, m = len(main), len(pattern)
if n <= m:
return 0 if main == pattern else -1
# bc
bc = [-1] * SIZE
generate_bc(pattern, m, bc)
# gs
suffix = [-1] * m
prefix = [False] * m
generate_gs(pattern, m, suffix, prefix)
i = 0
# 只要小于主字符串长度
while i < n-m+1:
j = m - 1
while j >-= 0:
if main[i+j] != pattern[j]:
break
else:
j -= 1
# pattern整个已匹配，返回
if j == -1:
return i
# 1、bc规则计算后移位数
x = j - bc[ord(main[i+j])]
# 2、gs规则计算后移位数
y = 0
if j != m-1: # 存在gs
y = move_by_gs(j, m, suffix, prefix)
i += max(x, y)
return -1
# 生成字符串哈希表
def generate_bc(pattern, m, bc):
for i in range(m):
bc[ord[pattern[i]]] = i
# 好前缀预处理
def generate_gs(pattern, m, suffix, prefix):
for i in range(m-1):
k = 0 # pattern[:i+1]和pattern的公共后缀长度
for j in range(i, -1, -1):
if pattern[j] == pattern[m-1-k]:
k += 1
suffix[k] == j
if j == 0:
prefix[k] == True
else:
break
# 通过好后缀计算移动值，存在三种情况：
# 1、整个好后缀在pattern扔能找到
# 2、好后缀存在 *后缀子串* 能和 pattern 的 *前缀* 匹配
# 3、其他
def move_by_gs(j, m, suffix, prefix):
k = m - 1 - j # j指向从后往前的第一个坏字符，k是此次匹配的好后缀的长度
if suffix[k] != -1: # 1. 整个好后缀在pattern剩余字符中仍有出现
return j - suffix[k] + 1
else:
for r in range(j+2, m): # 2. 后缀子串从长到短搜索
if prefix[m-r]:
return r
return m # 3. 其他情况
4、KMP算法
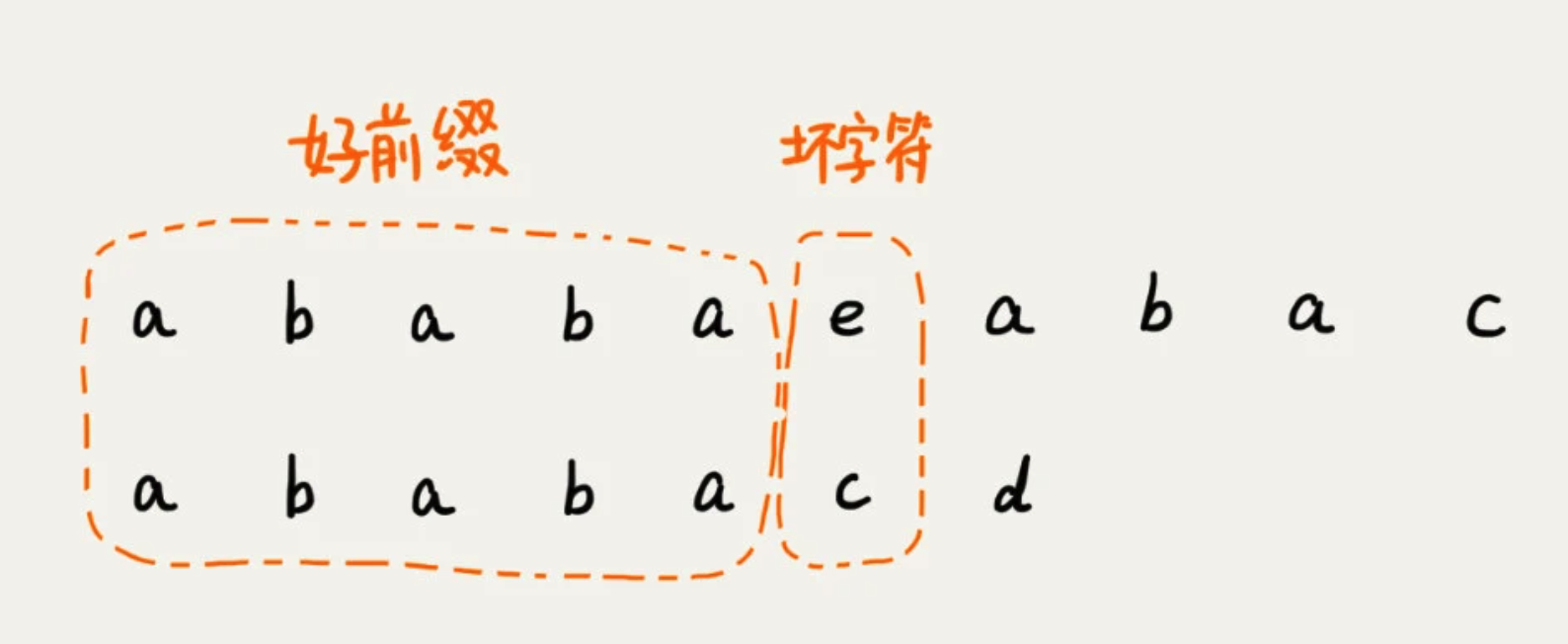
当遇到坏字符的时候，需要把模式串往后滑动。在滑动中，只要好前缀的后缀子串与模式串的前缀子串比较会更加高效。
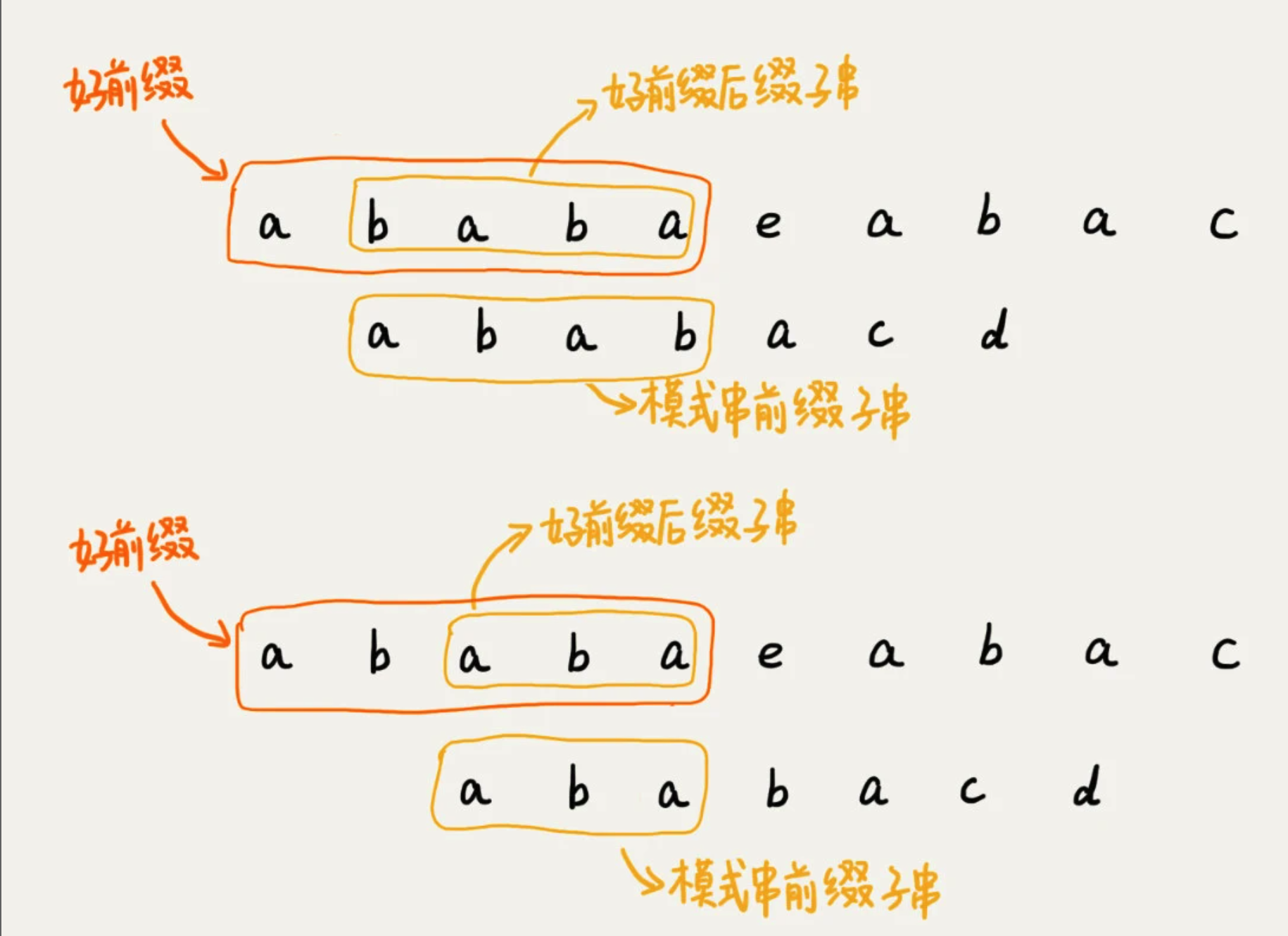
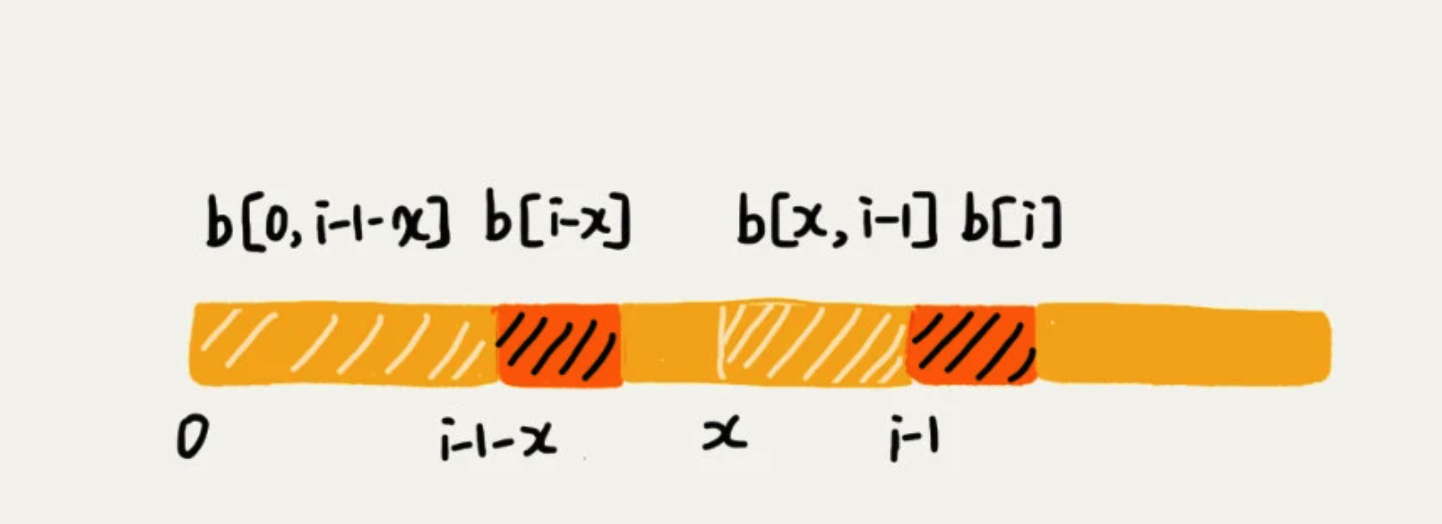
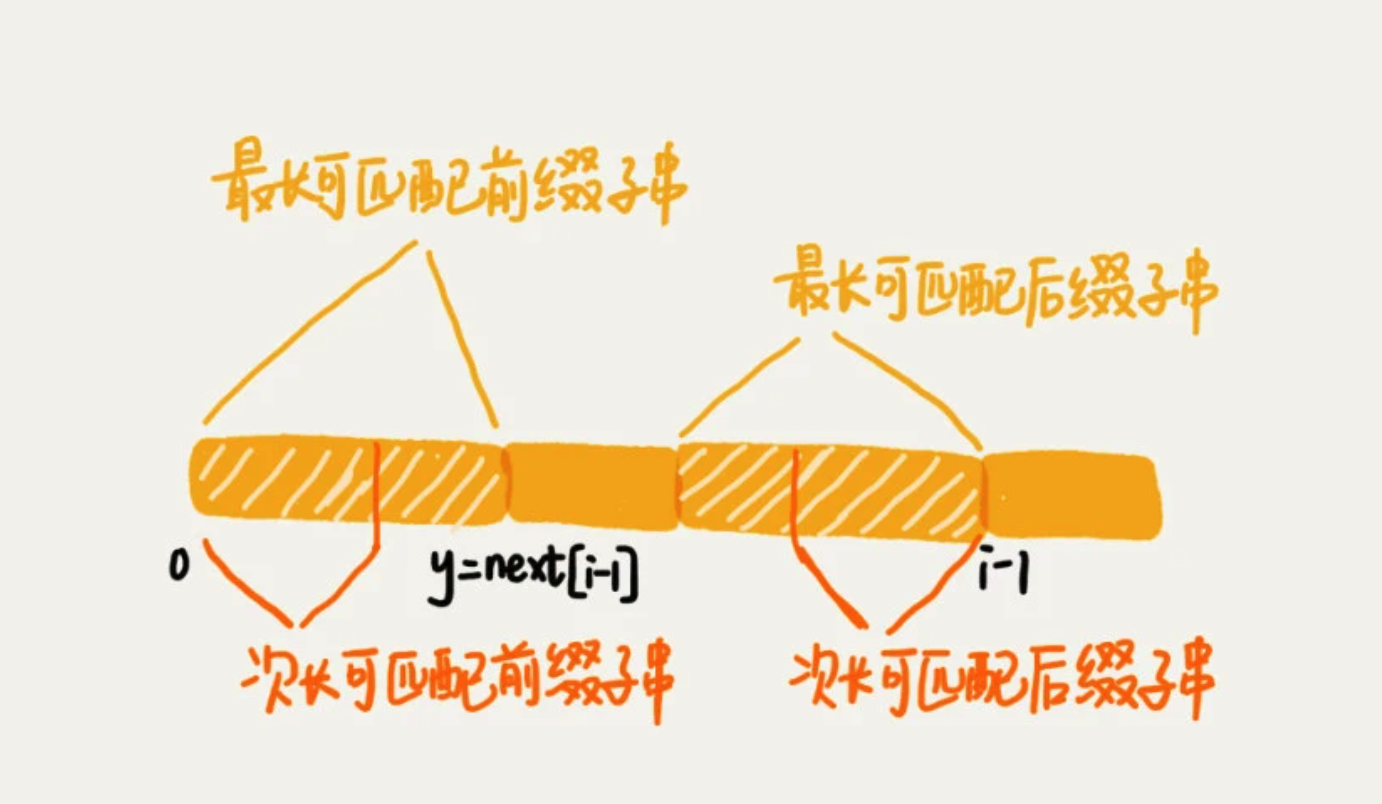
我们将好前缀的后缀子串中与 模式串 匹配最长的叫 最长可匹配后缀子串
对应的前缀子串，叫 最长可匹配的前缀子串
失效函数
构建一个数组，用来存储模式串中每个前缀的最长可匹配子串的结尾字符的下标，称为 next数组。又称 失效函数 failure function。
数组的下标是每个前缀结尾字符下标，数组的值就是这个前缀的最长可以匹配前缀子串的结尾下标。
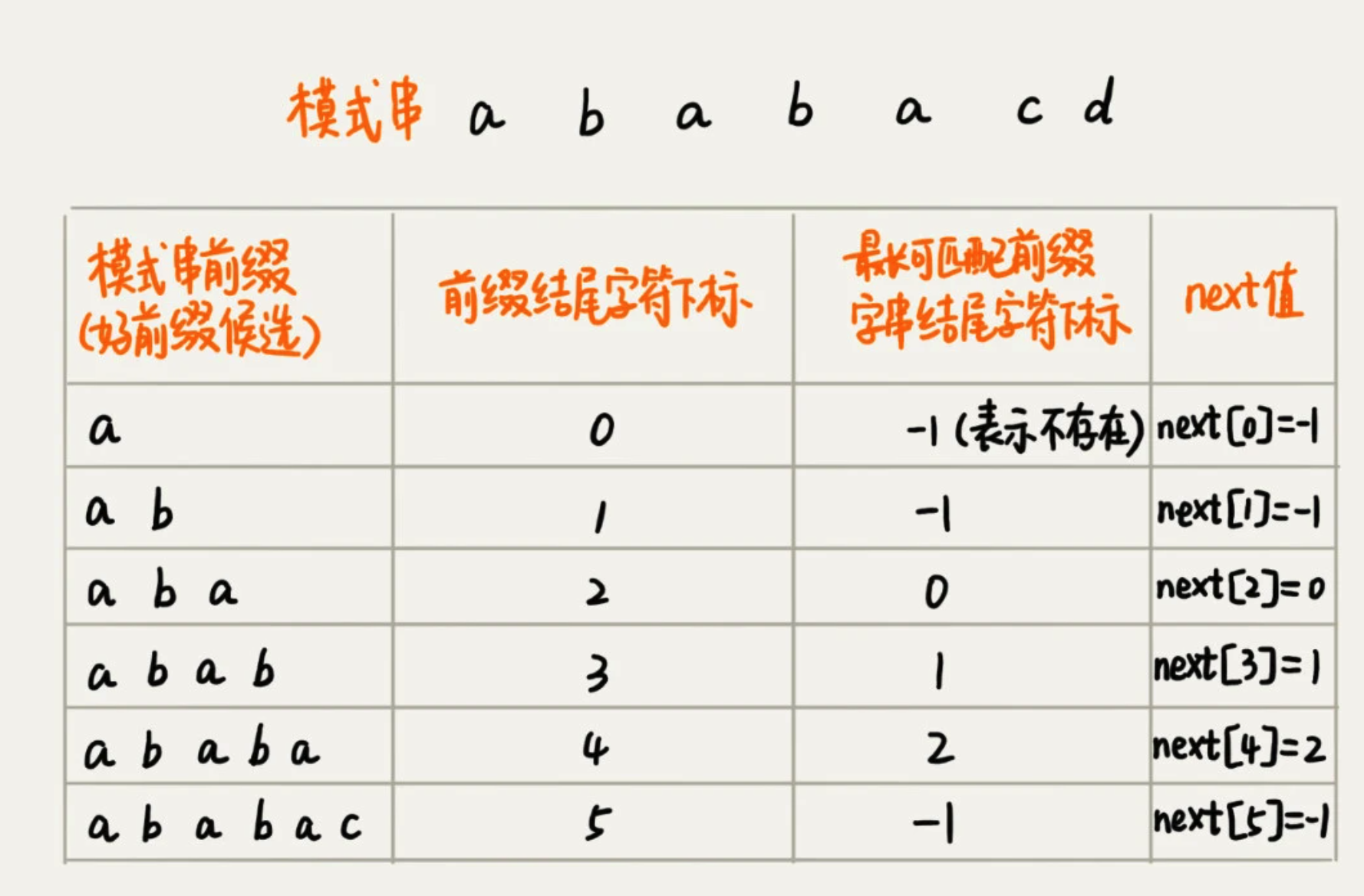
比如当模式串前缀是 a，那么它的后缀子串是空，所以next是-1
当模式串前缀是 a b a b a，那么它的后缀子串会存在四种情况，而与模式串的前缀子串匹配的右两个。
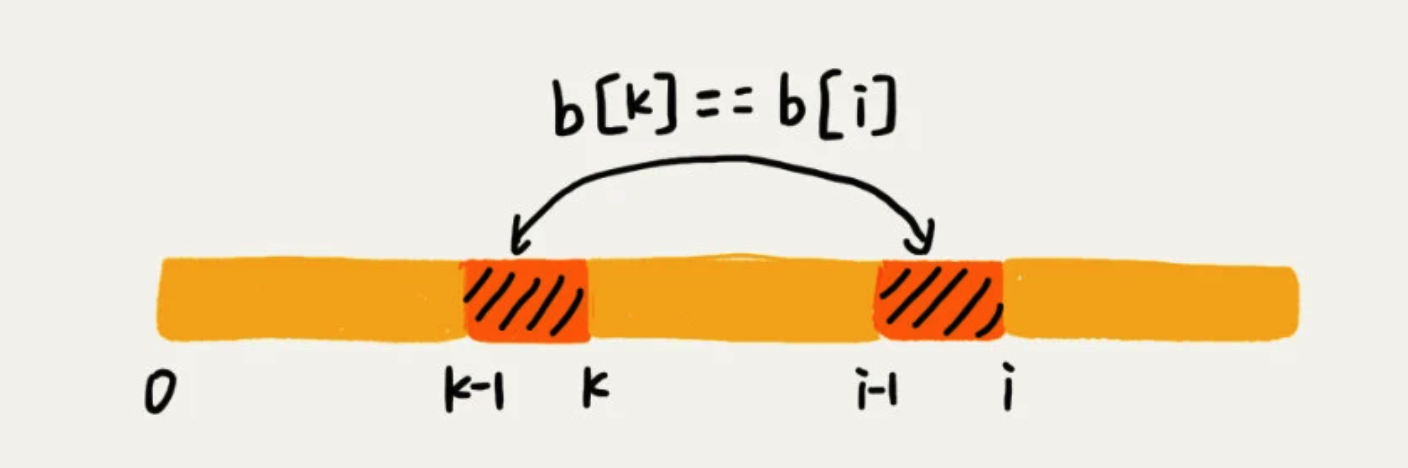
这种方法比较耗时，因此通过变量 i 和k来进行求
- 空间复杂度：O(m)，需要一个next数组，其大小跟模式串长度m相同
- 时间复杂度：O(m+n)，O(m)是next数组计算的耗时，O(n)是第二部分耗时
5、Tire树
也叫“字典树”，一种树形结构，专门处理字符串匹配的数据结构，用来解决一组字符串集合中快速查找某个字符串的问题。
有 6 个字符串，它们分别是：how，hi，her，hello，so，see。
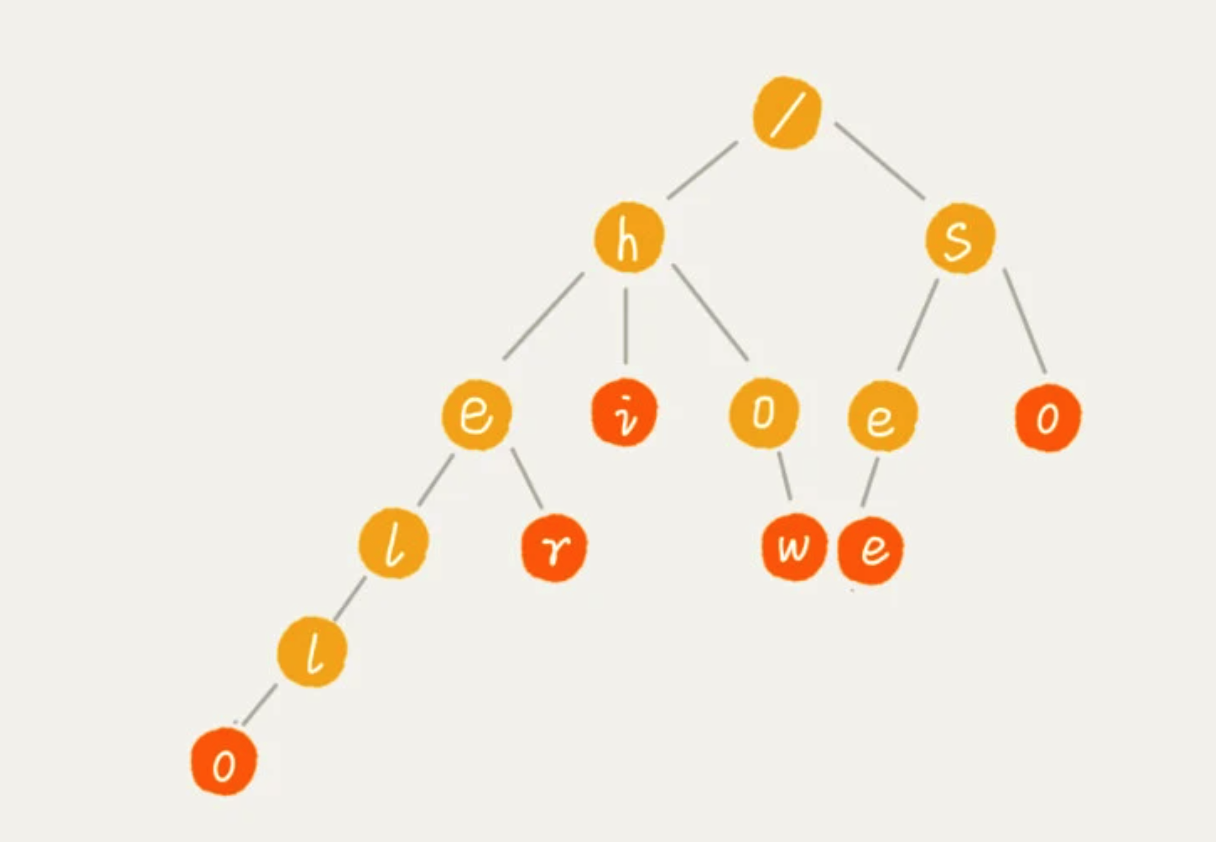
1、实现
通过一个下标与字符一一对应的数组，来存储子节点的指针。
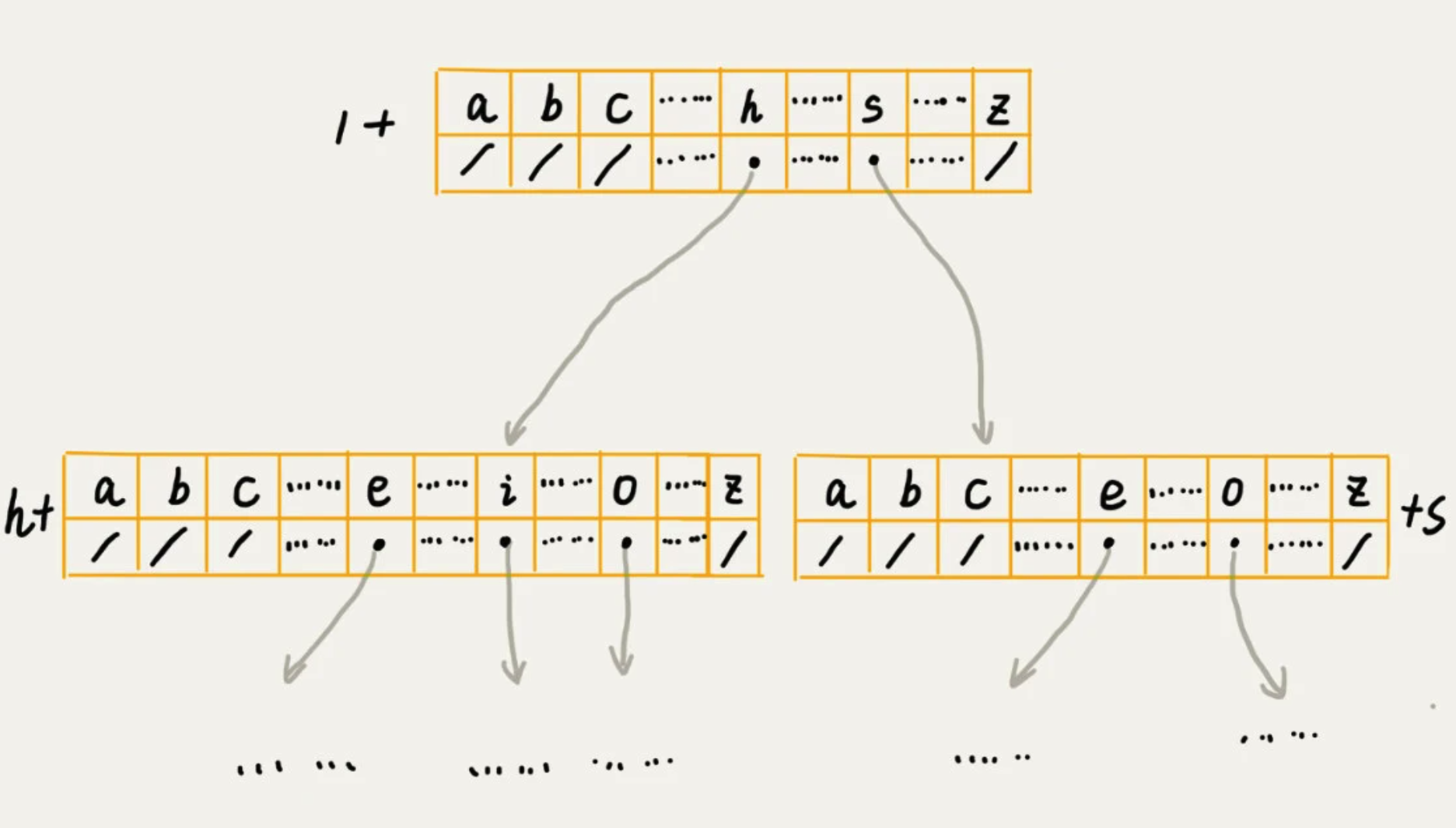
查找的时间复杂度，为 O(n)，n是所有字符串的长度和。
空间复杂度，取决于指针的存储方式。
6、AC自动机 Aho-Corasick
在Trie的基础上，加入类似 KMP 的 next数组。
1、构建
- 将多个模式串构建成 Trie树
- 在Tire上构建失败指针
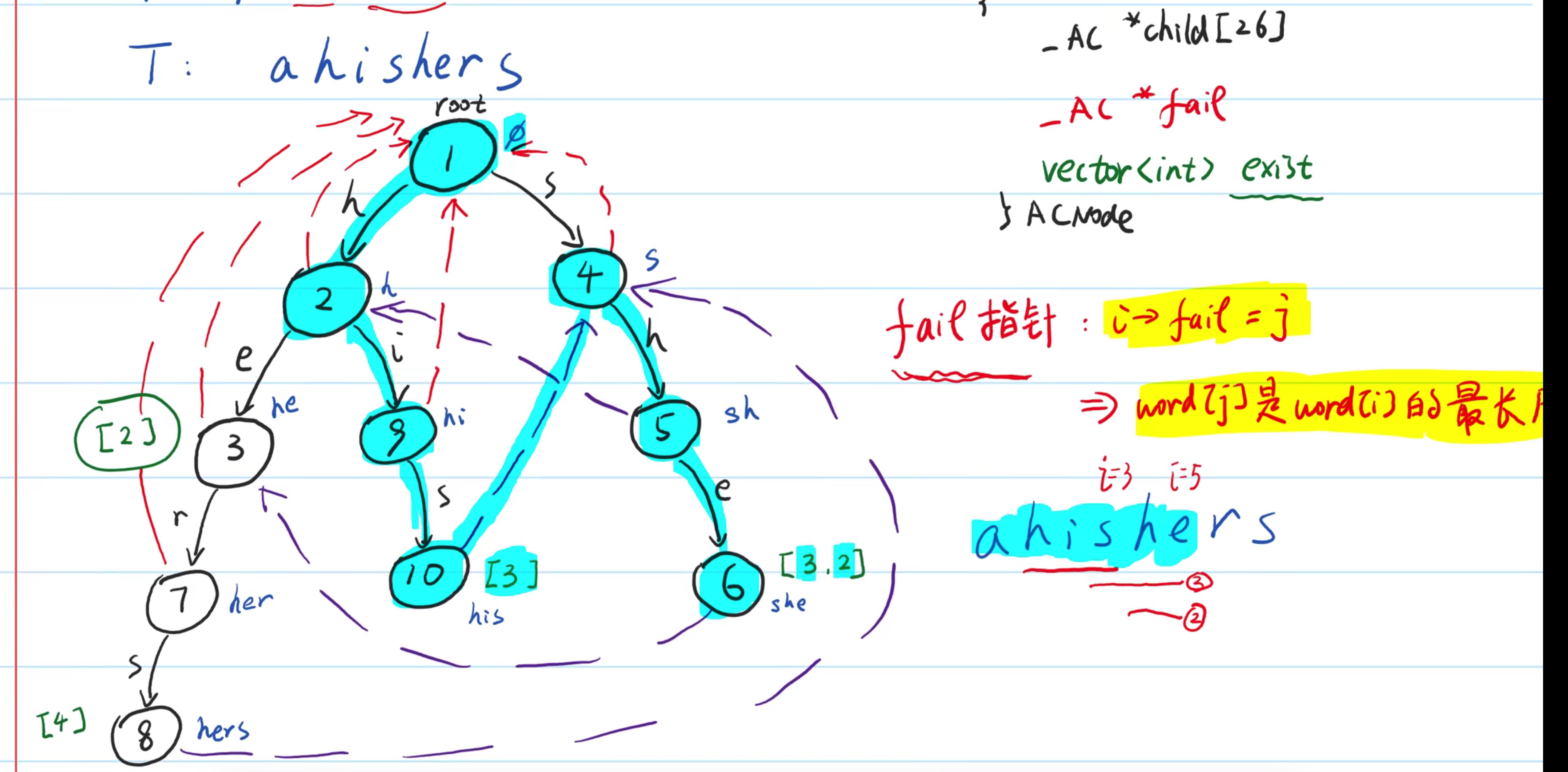
失败指针可以避免，匹配到一个模式串时，再用原来位置去匹配其他模式串。
浙公网安备 33010602011771号