第一单元表达式求导总结

第一单元表达式求导总结

三次作业分析

第一次作业

题目分析

​ 简单多项式导函数的求解，因子只有常数因子和幂函数，项内因子之间用乘号相连。表达式由若干个项加减组合。

实现方案

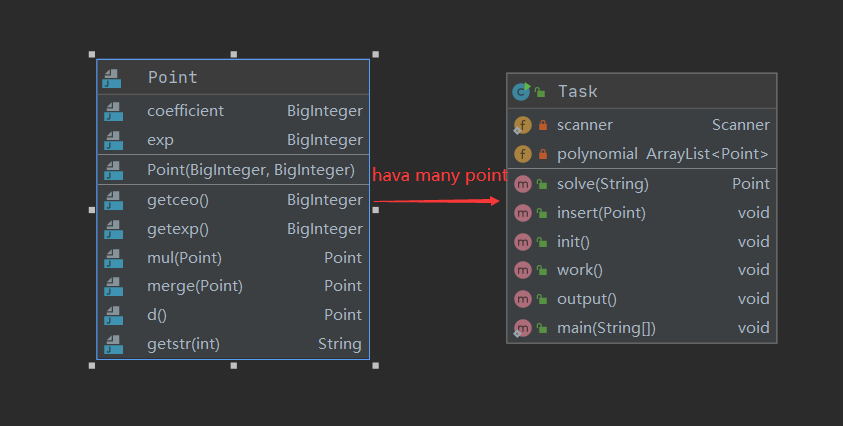
​ 我们知道一个项的最终形式一定是 \(a_i \times x^{b_i}\) ，所以我们创建一个记录项的类 point，支持合并，乘法和求导操作，表达式就是一个 point 的 arraylist ，每次加一个项先看能不能和已有的项合并，不行再加到 arraylist 中。

​ 接着就是输入字符串的处理，这次麻烦的是有空白字符和最多三个个加减符号在一起，我们可以用 String 中的 replaceall 函数把空白字符去掉，把 "++","+-+" 等换成相应的单个符号，最后把字符串用加减号分隔开，挨个处理项就可以了。

​ 最后是化简问题，相同指数的合并，首项的常数因子最好是正数，再注意一下常数是 \(\pm 1\)，指数是 \(1 \ or \ 0\) 的情况就可以了。（当时没有发现 \(x*x\) 比 \(x**2\) 更优）

结构分析

​ point 类实现项的各种运算方法，task类完成对多项式的读入和表达式的建立和求导

	属性个数	方法个数	代码规模
Point.java	2	6	107
Task.java	2	5	180

类图：

优点：项都是同一个类表示，项之间的运算和求字符串非常方便

缺点：Task类的复杂度很高，表达式的读入，计算，求导操作都在Task中，设计不合理。

BUG分析 && 心得体会

​ 第一次作业分数比较高，但是还是没有理解透面向对象的思想，按理应该再加一个poly类来实现多项式的处理。hack 就交了一个 有三加减符号的多项式 hack了两个人。但自己因为没有判断只有一个 0 的多项式导致没有输出，被 hack 了两次。

​ 经过这次作业后，我更多的是熟悉了 java 的基本语法和各种基本类的相关操作以及正则表达式的应用。研讨课同学的分析让我更深刻的理解了面向对象和从上而下的设计方法。这对我第二次作业有了巨大的帮助。

找bug

​ 这次结构比较简单，我看了两个人的代码都没有发现问题，就交了一个含有三个加减符号的较长的多项式，hack了两人。

第二次作业

题目分析

在上次的基础上增加了 \(sin(x)\) 和 \(cos(x)\) ，并且多了表达式因子，引入了括号。

实现方案

​ 这次新加的内容让我放弃了第一次作业的代码，之间经行重构。

​ 首先建立了一个抽象类 Func ，支持 求导，tostring 和 topoly（转为多项式），之后的类除了主函数Main之外都继承 Func ，首先是三个基本因子 \(a \times sin(x) ^b\) , \(a \times cos(x)^b\) , \(a \times x^b\) 。常数因子可以被理解为 \(a \times x^0\) 。之后是项 term ，内部是三个基本因子乘起来。多项式 poly 。内部有多个项的 加减。还有三个运算量 add , sub , mul ，代表 两个 Func 之间的操作。而最后的求导后的多项式则用每一个 Func 都用 topoly 转为多项式后经行统一的多显示运算，就是拆括号的写法。 这样的问题是化简非常困难，所以我放弃了化简操作。

​ 对于括号的问题我采用了转后缀表达式的做法，这样就可以把括号去掉然后建立表达式树。对树的根节点求导即可得到答案。

结构分析

	属性个数	方法个数	代码规模
Func.java	0	3	8
Mi.java	5	9	76
Sin.java	5	9	79
Cos.java	5	9	78
Term.java	7	10	240
Poly.java	1	8	86
Add.java	2	4	27
Sub.java	2	4	27
Mul.java	2	4	29
Main.java	10	8	245

类图

优点：每个类的功能清晰，可拓展性好。

缺点：term的因为要判断因子的种类，而且要对poly服务，导致代码冗长且复杂，加大了耦合性。

BUG分析

这次出现了三个bug，一个是后缀表达式处理出现了问题，我是直接参照高中写过的一个表达式求值的C代码写的，最后发现高中的代码居然写错了。第二个是处理字符串出现了问题，忽略了 (-( 这种形式带来的问题。最后Term中有一个Sin类写成了Cos类。前两个都出现在Main类中。这几个bug 提醒了我不能轻易相信中测和自己以前的代码，应该经行更多的测试。

找bug

就对我自己出现的问题构造了相关数据，又构造了一些表达式求导后比较复杂的数据。

第三次作业

题目分析

sin 和 cos 里面也可以是表达式，加入了格式审查。

实现方案

和第二次作业非常相似，就可以在第二次代码的基础上经行改动就可以了。

我修改了 Sin 和 Cos 类的内部结构，把用一个 Func 变量来保存括号里的表达式。同时改变了输出字符串的算法，改为不拆括号的写法。比起第二次作业的推到重来要轻松了不少。

结构分析

	属性个数	方法个数	代码规模
Func.java	0	3	8
Mi.java	5	9	100
Sin.java	6	9	106
Cos.java	6	9	106
Term.java	7	10	240
Poly.java	1	8	86
Add.java	2	4	27
Sub.java	2	4	27
Mul.java	2	4	29
Main.java	10	8

类图 （和第二次一致）

优点：和第二次基本一致

缺点：main函数变得更长了，我对格式审查，处理后缀表达式的做法都是面向过程的，之后遇到别的类似问题需要重构相关代码。

BUG分析

由于后缀表达式的做法很难有方法去找出各种各样的格式审查错误。我只能尽可能的枚举我能想出的典型格式错误，然后用正则表达式去匹配相应的错误是否出现。想要彻底修复需要用递归下降算法去检查格式。

找bug

Hack: 0 / 7，太菜了完全找不出bug。

重构经历总结

我的重构发生在第二次作业，第一次的结构过于简单，我又在研讨课上和第二次作业指导书中得到了启发，重新建立了一个比较合理，扩展性好的结构，这对我第三次作业的完成提供了很大的便利，重构前后的区别天翻地覆，没有对比分析的价值。

心得体会

​ 这几次作业让我更进一步的理解了面向对象的思想，第二次转第三次作业的便利也让我知道了面向对象的重要性。几次强侧和互测也有了一些反思,检查代码千万不能面向评测机或者自己随便测几组样例，BUG往往藏在一些比较偏僻的数据中。