[AcWing 3409] 这是一棵树吗

并查集 + 树的判定

---

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e4 + 10;

int n;
int p[N];

int find(int x)
{
    if (p[x] != x)
        p[x] = find(p[x]);
    return p[x];
}

void merge(int a, int b)
{
    int pa = find(a), pb = find(b);
    p[pa] = pb;
}

void solve()
{
    for (int Case = 1; ; Case ++) {
        // vis记录点的个数，ind记录点的入度
        vector<int> vis(N), ind(N);
        int a, b, m = 0;
        bool ok = true;
        for (int i = 0; i < N; i ++)
            p[i] = i;
        while (cin >> a >> b, a > 0) {
            // 形成环
            if (find(a) == find(b))
                ok = false;
            else
                merge(a, b);
            vis[a] = vis[b] = 1;
            // 点的入度为2
            if (ind[b])
                ok = false;
            else
                ind[b] = 1;
            m ++;
        }
        if (a == -1)
            break;
        int num = count(vis.begin(), vis.end(), 1);
        // 不满足 点的个数 = 边的个数 + 1
        if (m + 1 != num && m)
            ok = false;
        if (ok)
            printf("Case %d is a tree.\n", Case);
        else
            printf("Case %d is not a tree.\n", Case);
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    solve();

    return 0;
}

---

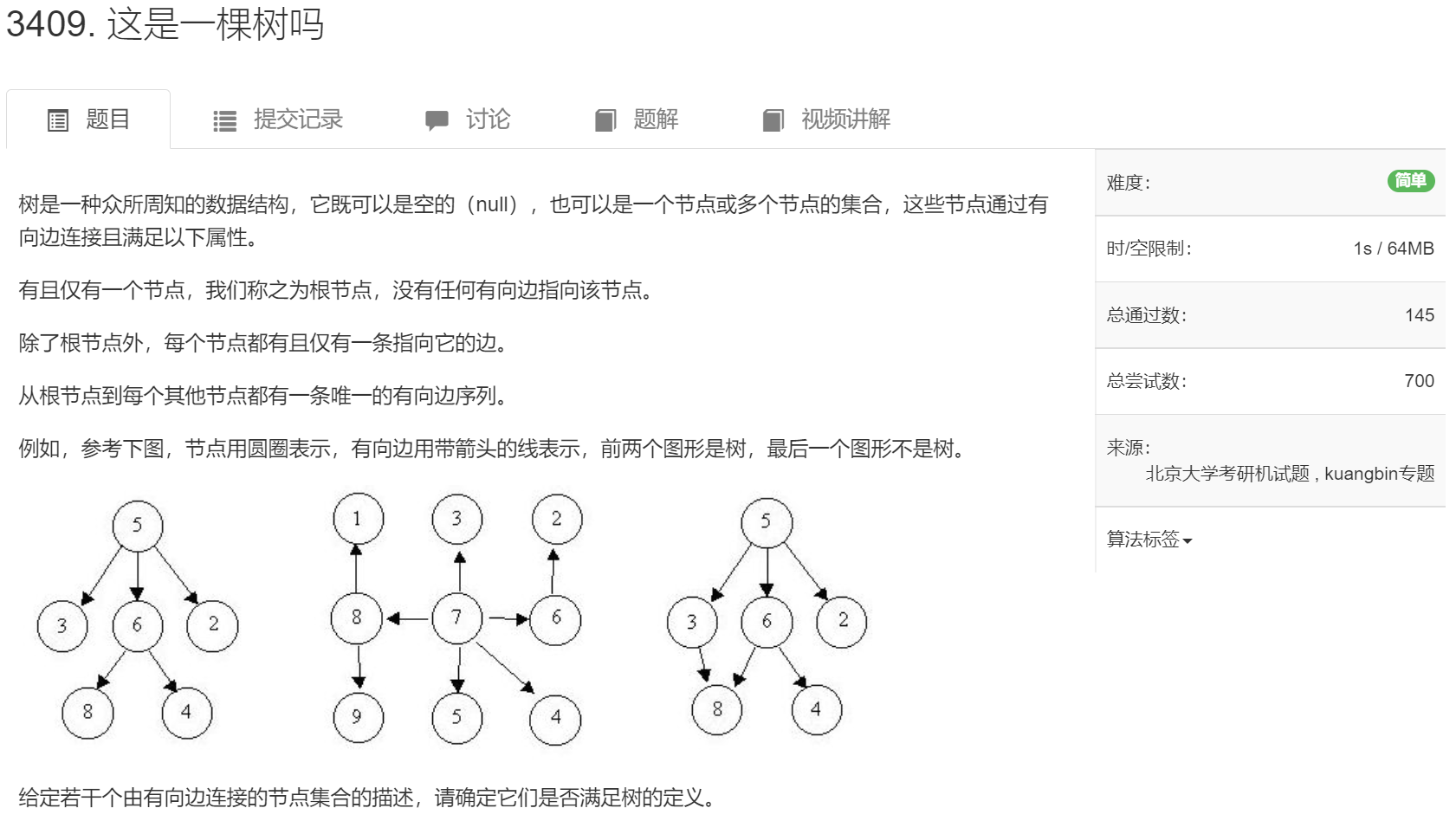
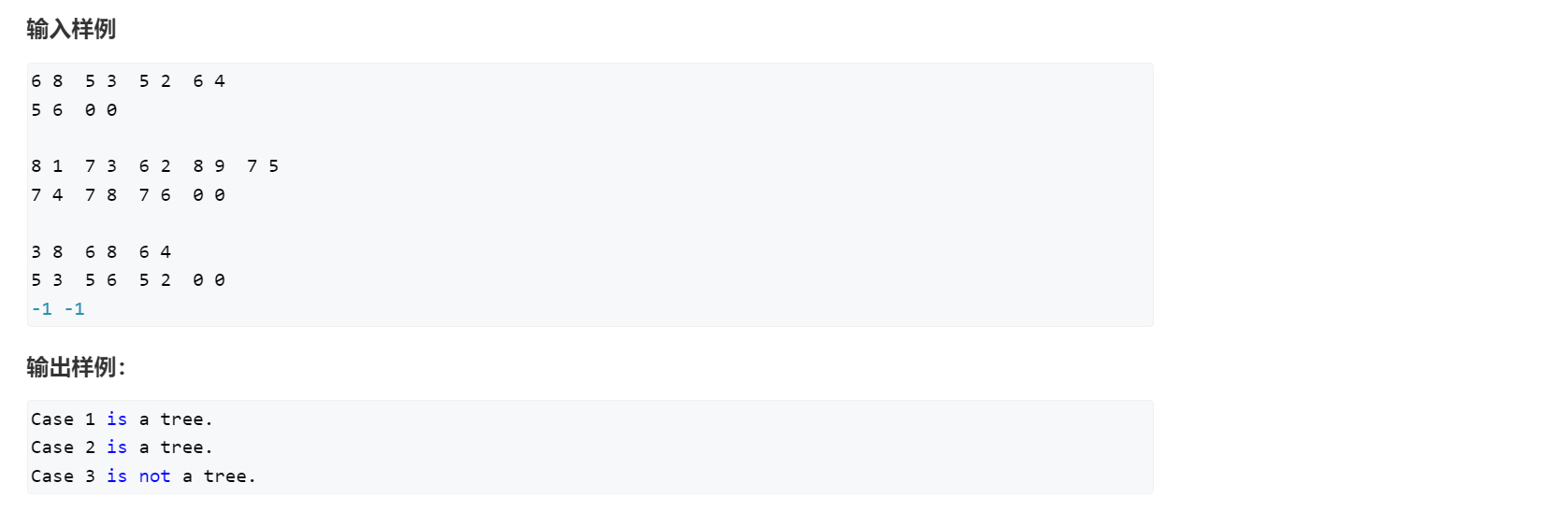
1. 如何判断是不是一颗树：
   ① 没有环 \(\rightarrow\) 在添加边之前，判断两点是否已经属于同一集合
   ② 每个节点最多只有一个入度 \(\rightarrow\) 用 \(ind\) 记录每个点的入度
   ③ 边数 \(+ 1 =\) 点数 \(\rightarrow\) 用 \(vis[i]\) 记录是否有 \(i\) 点，点的总个数等于 \(vis\) 中 \(1\) 的个数，总边数就是输入的边的个数