[AcWing 1114] 棋盘问题

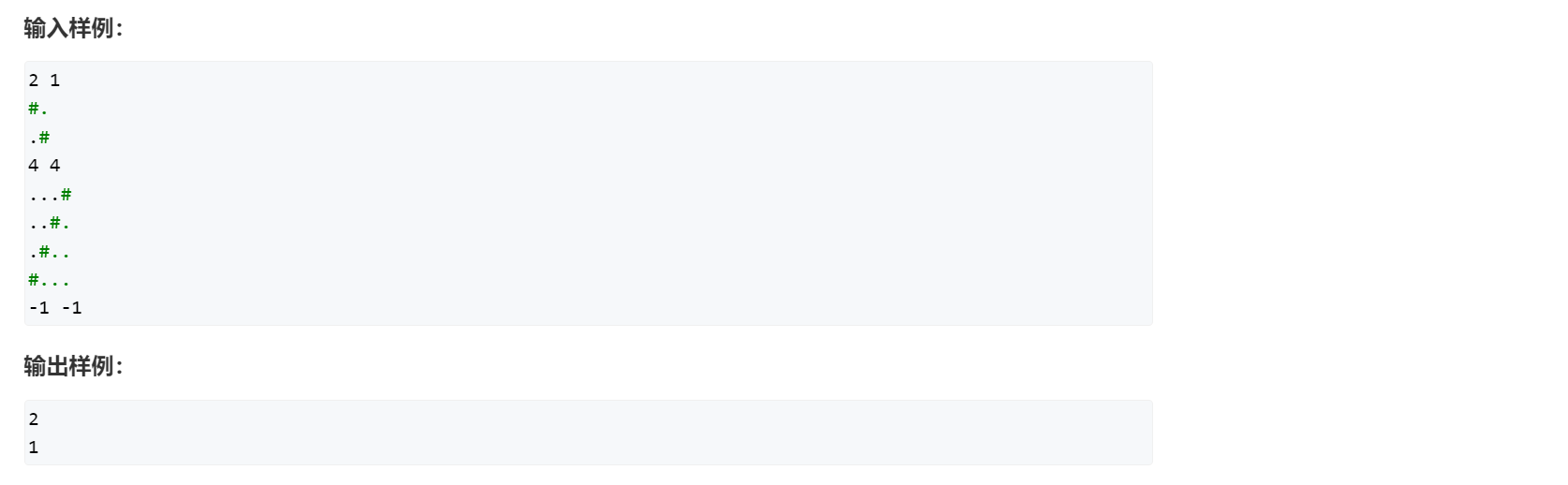
八皇后问题的变形

$DFS$ 按行枚举

---

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 10 + 10;

int n, m;
char g[N][N];
bool col[N];
int res;

// u 表示第几行，num 表示放了几个棋子
void dfs(int u, int num)
{
    // 已经放了 m 个棋子
    if (num == m) {
        res ++;
        return;
    }

    // 已经超过了棋盘边界
    if (u == n)
        return;

    // 这一行不放棋子
    dfs(u + 1, num);

    // 这一行放棋子
    for (int i = 0; i < n; i ++)
        if (g[u][i] == '#' && !col[i]) {
            col[i] = true;
            dfs(u + 1, num + 1);
            col[i] = false;
        }
}

void solve()
{
    while (cin >> n >> m, n != -1) {
        for (int i = 0; i < n; i ++)
            cin >> g[i];
        res = 0;
        // 从第 0 行，放了 0 个棋子开始搜
        dfs(0, 0);
        cout << res << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    solve();

    return 0;
}

---

1. 按行枚举，$DFS$ 有两个参数，一个表示在第 $u$ 行，一个表示已经放了 $num$ 个棋子
2. 与八皇后的一大不同之处：对于 $DFS(u, num)$，第 $u$ 行可以不放棋子，即直接递归 $DFS(u + 1, num)$