[AcWing 245] 你能回答这些问题吗

线段树

单点修改，区间查询（子段和的最大值）

---

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 5e5 + 10;

int n, m;
int w[N];

struct Node {
    int l, r;
    int sum, lmax, rmax, tmax;
} tr[N * 4];

void pushup(Node &u, Node &l, Node &r)
{
    u.sum = l.sum + r.sum;
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r)
{
    if (l == r) {
        tr[u] = {l, r, w[l], w[l], w[l], w[l]};
        return;
    }
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void update(int u, int x, int v)
{
    if (tr[u].l == tr[u].r) {
        tr[u] = {x, x, v, v, v, v};
        return;
    }
    int mid = tr[u].l + tr[u].r >> 1;
    if (x <= mid)
        update(u << 1, x, v);
    else
        update(u << 1 | 1, x, v);
    pushup(u);
}

Node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
        return tr[u];
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid)
        return query(u << 1, l, r);
    else if (l > mid)
        return query(u << 1 | 1, l, r);
    else {
        auto left = query(u << 1, l, r);
        auto right = query(u << 1 | 1, l, r);
        Node res;
        pushup(res, left, right);
        return res;
    }
}

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)
        cin >> w[i];
    build(1, 1, n);
    while (m --) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            if (x > y)
                swap(x, y);
            cout << query(1, x, y).tmax << endl;
        }
        else
            update(1, x, y);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    solve();

    return 0;
}

---

1. 维护区间子段和的最大值
   设当前节点为 \(u\)，左孩子是 \(l\)，右孩子是 \(r\)
   \(u\) 的子段最大值有三种可能取值：
   ① \(l\) 的子段最大值
   ② \(r\) 的子段最大值
   ③ 横跨 \(l\) 和 \(r\) 的区间的最大值，即 \(l\) 的后缀最大值 + \(r\) 的前缀最大值
   因此还需要维护区间的后缀最大值和前缀最大值，用 \(lmax\) 表示前缀最大值，\(rmax\) 表示后缀最大值，\(sum\) 表示区间的总和
   \(u.sum = l.sum + r.sum\)
   \(u.lmax = max(l.lmax, l.sum + r.lmax)\)
   \(u.rmax = max(r.rmax, r.sum + l.rmax)\)
   用 \(tmax\) 表示子段和的最大值
   \(u.tmax = max(l.tmax, r.tmax, l.rmax + r.lmax)\)
2. 查询操作
   
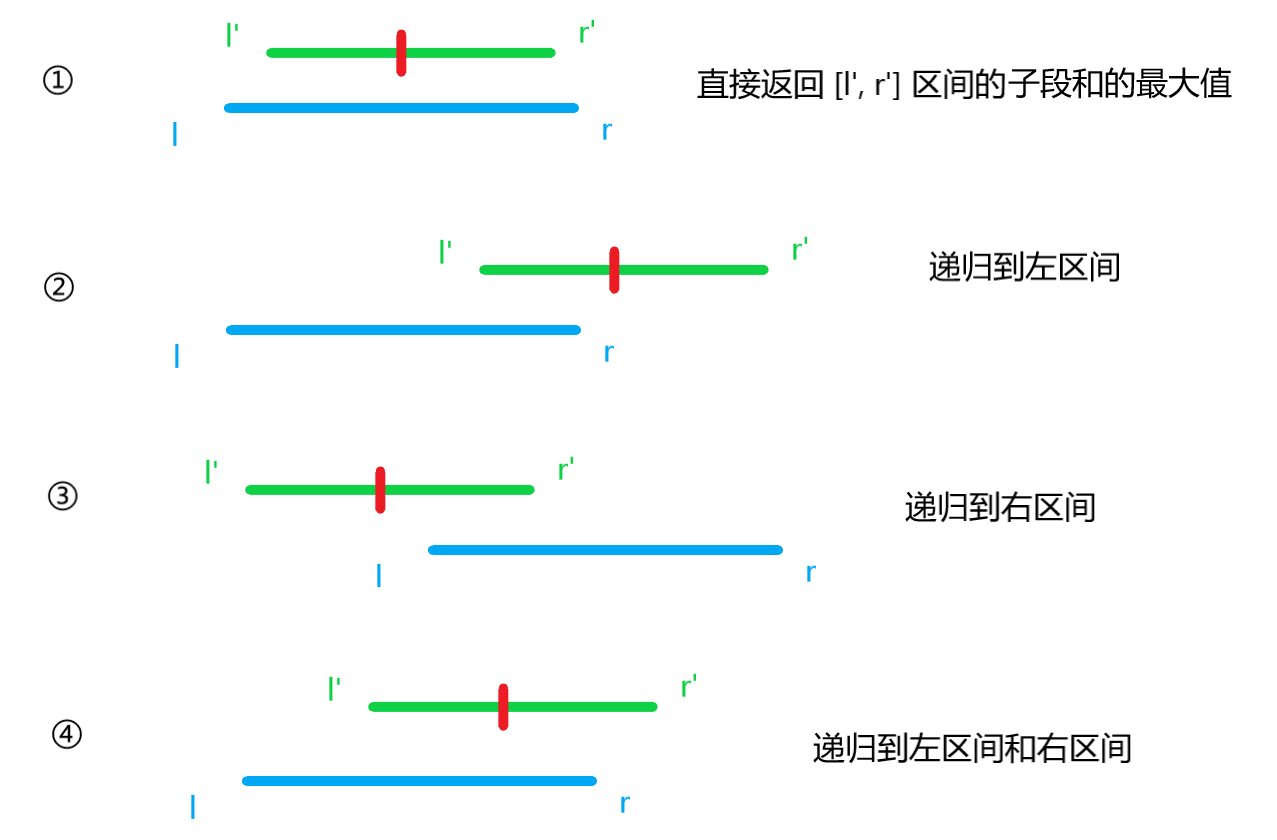
   有哪一段还没算，就要递归调用包含这一段的区间