[AcWing 243] 一个简单的整数问题2 (树状数组)

树状数组

区间修改，区间查询

---

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 2e5 + 10;

int n, m;
LL a[N];
LL tr1[N], tr2[N];

int lowbit(int x)
{
    return x & -x;
}

void add(LL tr[], int x, LL c)
{
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += c;
}

LL ask(LL tr[], int x)
{
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

LL get(int x)
{
    LL res = ask(tr1, x) * (x + 1) - ask(tr2, x);
    return res;
}

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
    for (int i = 1; i <= n; i ++) {
        LL b = a[i] - a[i - 1];
        add(tr1, i, b);
        add(tr2, i, 1LL * i * b);
    }
    while (m --) {
        char op;
        int l, r, d;
        cin >> op >> l >> r;
        if (op == 'C') {
            cin >> d;
            add(tr1, l, d);
            add(tr1, r + 1, -d);
            add(tr2, l, l * d);
            add(tr2, r + 1, (r + 1) * (-d));
        }
        else
            cout << get(r) - get(l - 1) << endl;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    solve();

    return 0;
}

---

1. 用 $b[i]$ 表示 $a[i]$ 的差分数组，即 $b[i] = a[i] - a[i - 1]$，维护 $b[i]$ 和 $i * b[i]$ 的前缀和，理由如下
   由于需要求区间的和，所以需要求出任意一点处的前缀和 $\sum_{i = 1}^{x} \sum_{j = 1}^{i} b[j]$
   将前缀和写成以下形式
   
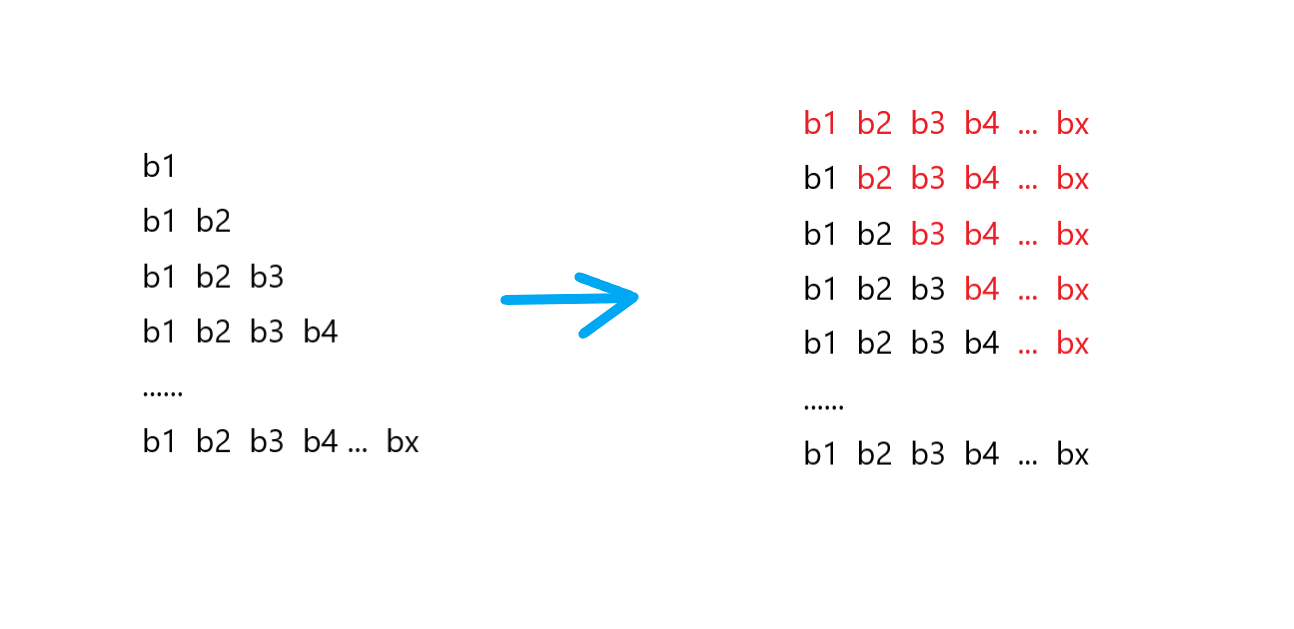
   $\sum_{i = 1}^{x} \sum_{j = 1}^{i} b[j] = (x + 1) \cdot \sum_{i = 1}^{x} b[i] - \sum_{i = 1}^{x} i * b[i]$