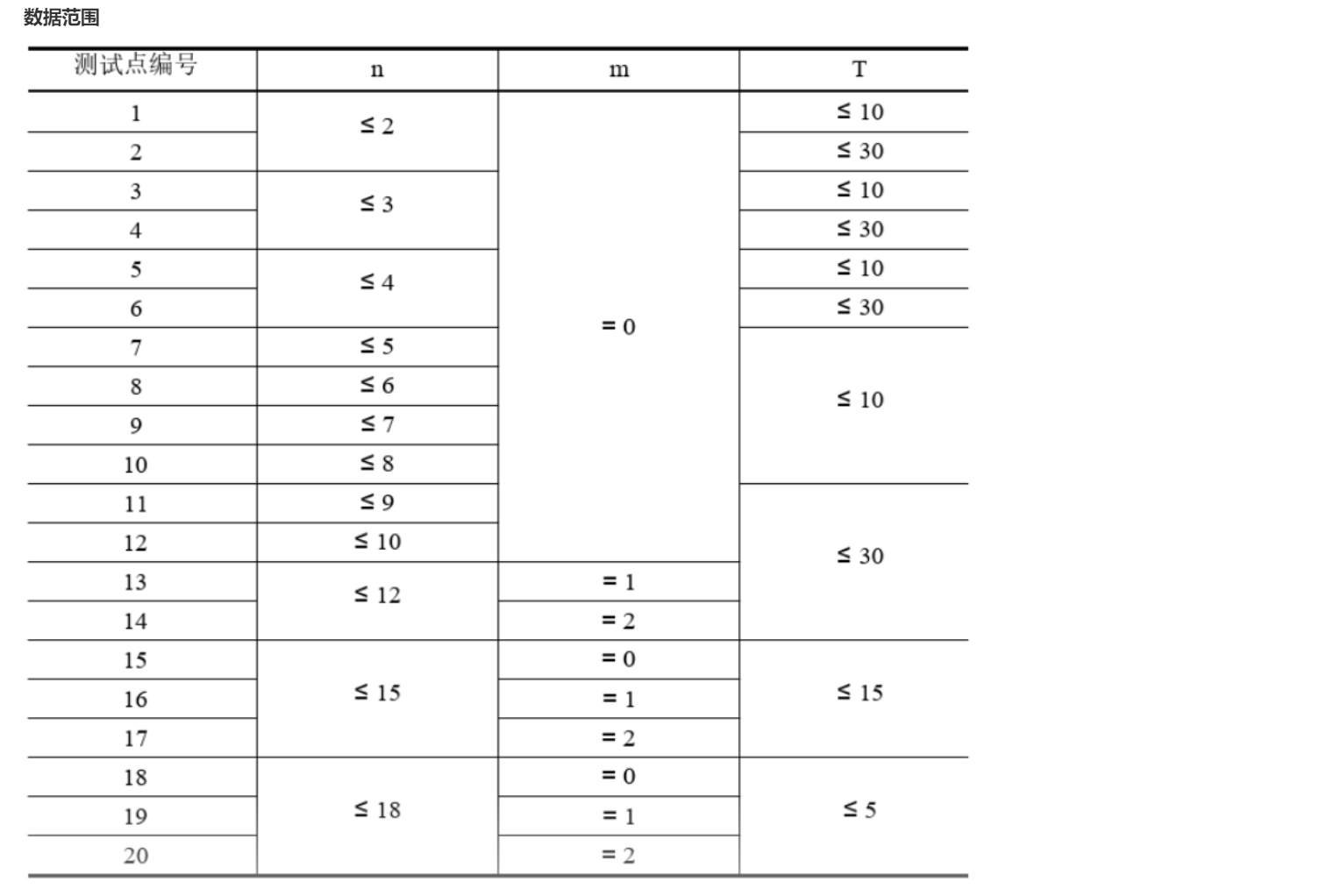
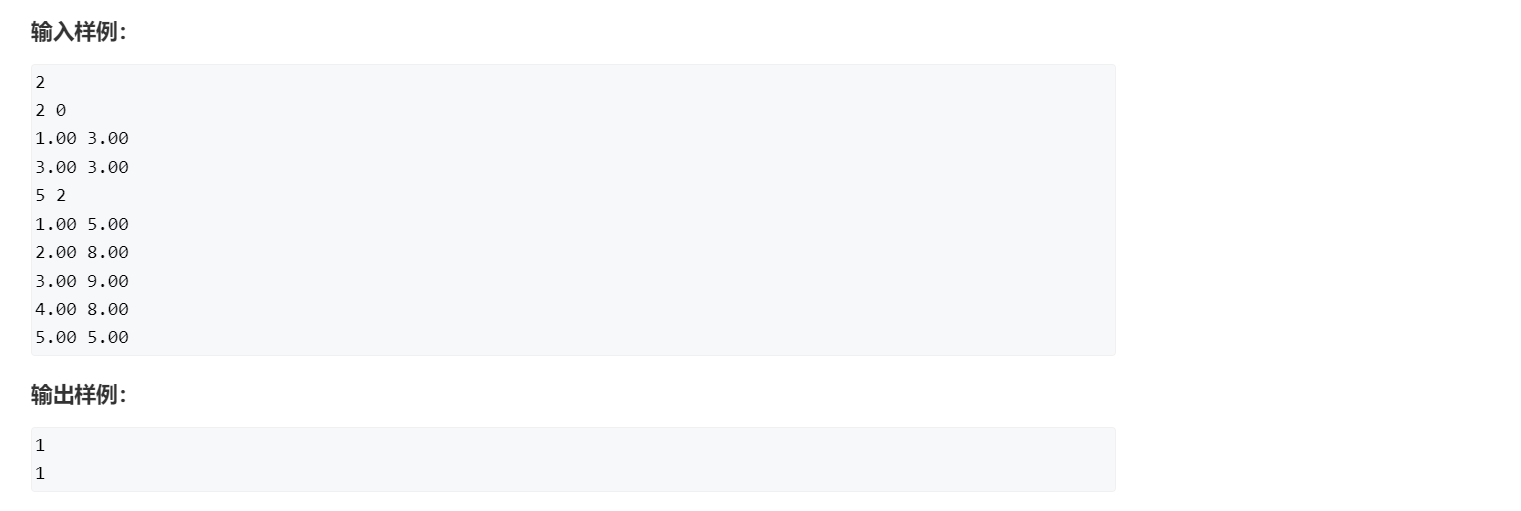
[AcWing 524] 愤怒的小鸟

---

点击查看代码

#include<iostream>
#include<cstring>
#include<vector>
#include<cmath>

using namespace std;

const int N = 18, M = 1 << N;

int n, m;
int path[N][N];
int f[M];

struct Position
{
    double x, y;
}p[N];

bool equal(double a, double b)
{
    return fabs(a - b) < 1e-6;
}

void solve()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++)
        cin >> p[i].x >> p[i].y;
    memset(path, 0, sizeof path);
    for (int i = 0; i < n; i ++) {
        path[i][i] = 1 << i;
        for (int j = 0; j < n; j ++) {
            double x1 = p[i].x, y1 = p[i].y;
            double x2 = p[j].x, y2 = p[j].y;
            if (equal(x1, x2))
                continue;
            double a = (y1 / x1 - y2 / x2) / (x1 - x2);
            double b = y1 / x1 - a * x1;
            if (a >= 0)
                continue;
            int state = 0;
            for (int k = 0; k < n; k ++) {
                double x = p[k].x, y = p[k].y;
                if (equal(a * x * x + b * x, y))
                    state += 1 << k;
            }
            path[i][j] = state;
        }
    }
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    for (int i = 0; i + 1 < 1 << n; i ++) {
        int x = 0;
        for (int j = 0; j < n; j ++)
            if ((i >> j & 1) == 0) {
                x = j;
                break;
            }
        for (int j = 0; j < n; j ++)
            f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1);
    }
    cout << f[(1 << n) - 1] << endl;
}

int main()
{
    int T;
    cin >> T;
    while (T --) {
        solve();
    }
    return 0;
}

---

1. 预处理
   任取两点 $(x_1,y_1),(x_2,y_2)$，求出过两点的抛物线，为了能形成抛物线，需要满足 $x_1 \neq x_2$，题目要求 $a < 0$，形成的抛物线 $y = a \cdot x^2 + b \cdot x$，如果 $a \geqslant 0$，也是不合法的，对于满足要求的抛物线，枚举每一个点，用二进制数来表示每一个点是否在 $(x_1,y_1),(x_2,y_2)$ 所形成的抛物线上
2. 求抛物线的参数
   对于 $y = a \cdot x^2 + b \cdot x$，过 $(x_1,y_2),(x_2,y_2)$，得到方程组
   $y_1 = a\cdot x_1^2 + b \cdot x_1$ $\rightarrow$ $\frac{y_1}{x_1} = a\cdot x_1 + b$
   $y_2 = a\cdot x_2^2 + b \cdot x_2$ $\rightarrow$ $\frac{y_2}{x_2} = a\cdot x_2 + b$
   解得 $a = \frac{ \frac{y_1}{x_1} - \frac{y_2}{x_2} }{x_1 - x_2}$，$b = \frac{y_1}{x_1} - a \cdot x_1$
3. 状态表示
   $s$ 是一个二进制数，位上为 $1$ 表示抛物线已经包含这一点
   $f[s]$ 表示状态为 $s$ 所需的最少抛物线个数
4. 状态计算
   对于每一个 $s$，找到未包含的一个点，即找到位上为 $0$ 的位置，需要加一条过该位置的抛物线，抛物线过的另一个点是任意的，枚举所有情况，更新此时包含的点所需的最小抛物线个数
   $f[i \ | \ path[x][j]] = min(f[i] + 1)$
5. 最终的结果
   $f[(1 << n) - 1]$，即 $n$ 位都为 $1$，表示包含了全部的点