[AcWing 4484] 有限小数

---

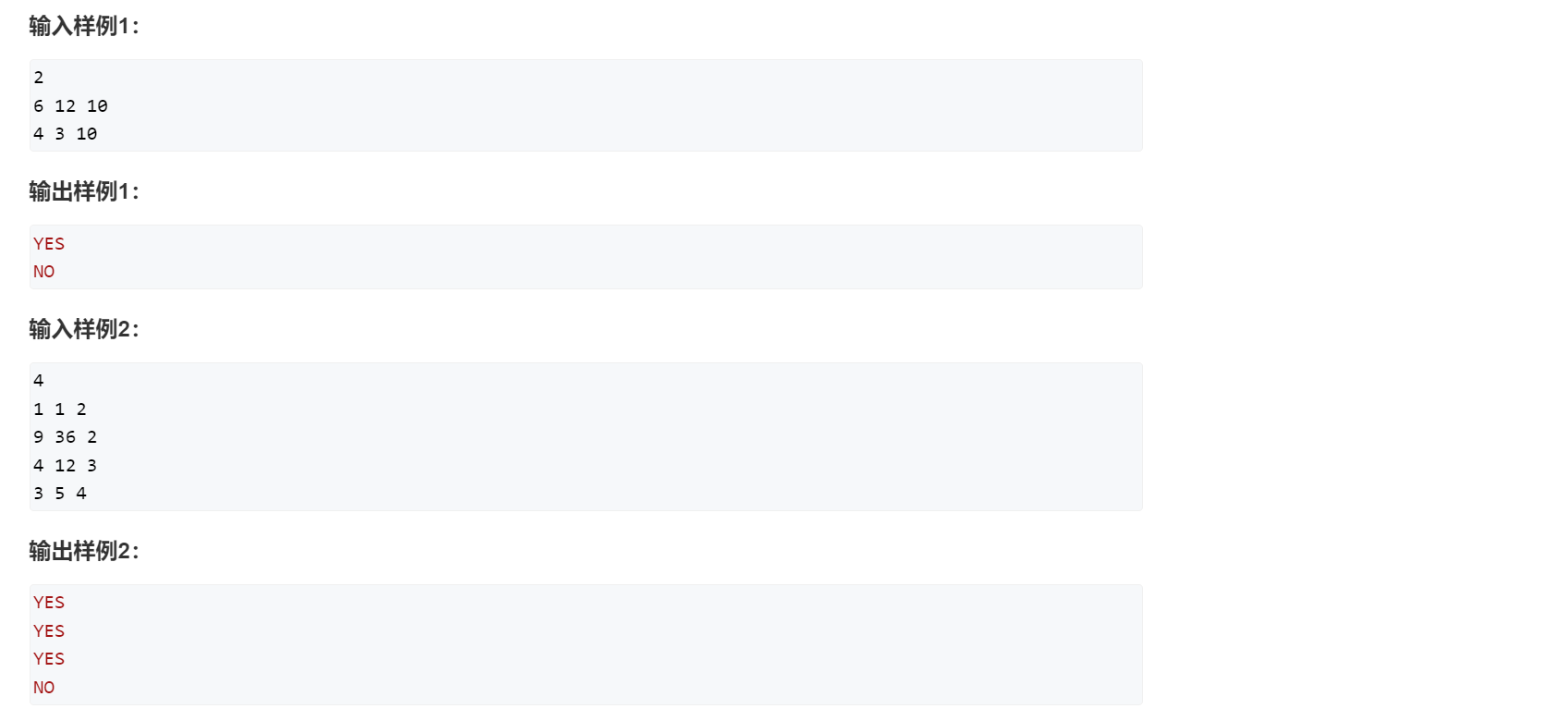
点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

void solve()
{
    LL p, q, b;
        scanf("%lld %lld %lld", &p, &q, &b);
        LL d = __gcd(p, q);
        q /= d;
        while (q > 1) {
            d = __gcd(q, b);
            if (d == 1)
                break;
            while (q % d == 0)
                q /= d;
        }
        if (q == 1)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
}

int main()
{
    // ios::sync_with_stdio(false);
    // cin.tie(nullptr);

    int T;
    cin >> T;
    while (T --) {
        solve();
    }

    return 0;
}

---

1. 等价命题
   $\frac{p}{q}$ 在 $b$ 进制下能用 $k$ 位小数表示 $\Leftrightarrow$ $q \mid b^{k}$
   ① 充分性：若 $\frac{p}{q}$ 在 $b$ 进制下是有限小数，则 $\frac{p}{q}$ 可以写成这样的形式，$\frac{p}{q} = z + a_1 \cdot b^{-1} + a_2 \cdot b^{-2} + \cdots + a_k \cdot b^{-k}$ ($z$ 代表一个整数)，等式两边都乘以 $b^{k}$，得到 $p \cdot \frac{b^{k}}{q} = z'$ ($z'$ 代表一个整数)，进而推出 $q \mid b^{k}$