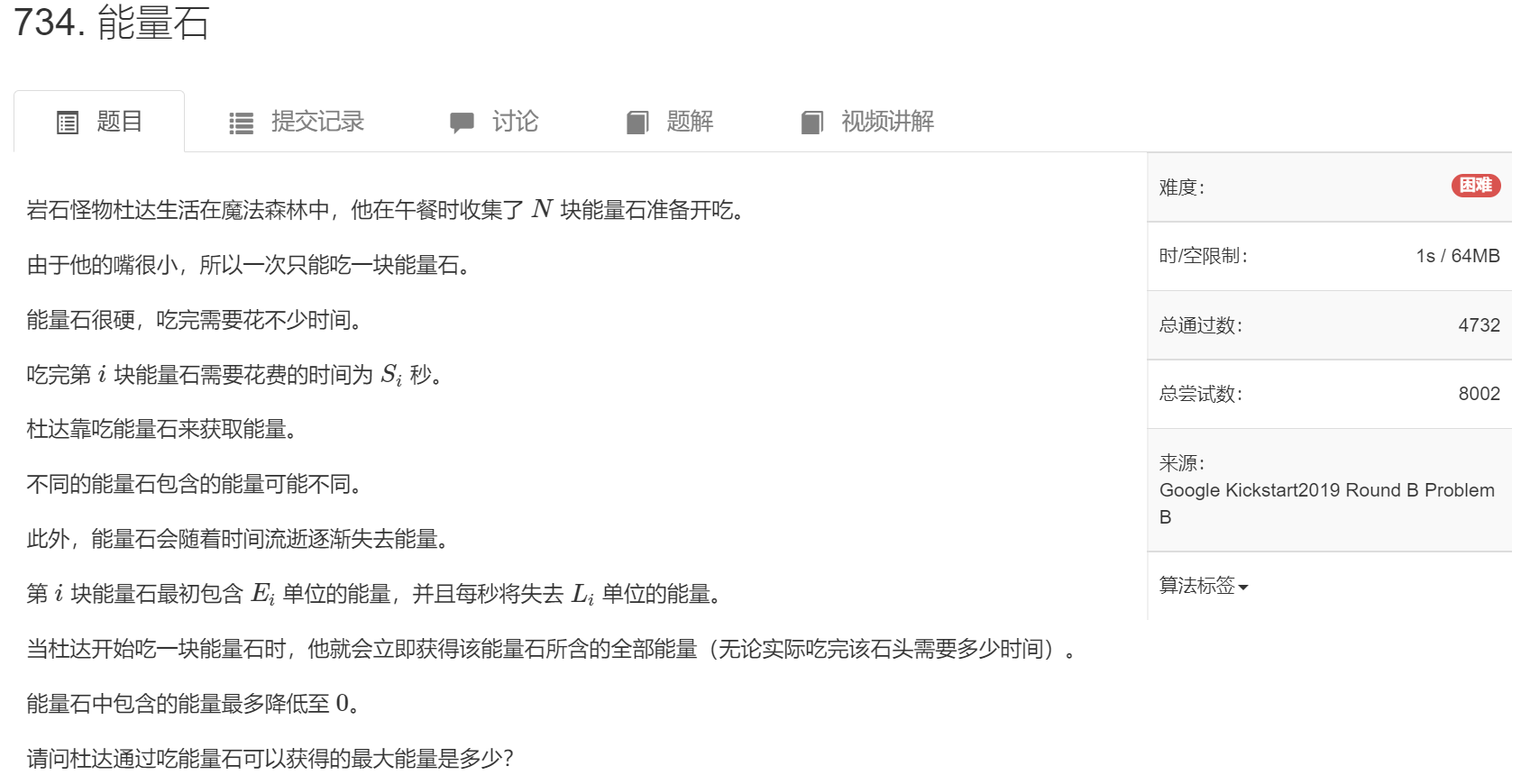
[AcWing 734] 能量石

贪心 + 01背包模型

---

点击查看代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 10010; 

int n;
int f[N];

struct Stone {
	int s, e, l;
	bool operator < (const Stone &W) const {
		return s * W.l < l * W.s;
	}
}stone[N];

int main()
{
	int T;
	cin >> T;
	for (int C = 1; C <= T; C ++) {
		cin >> n;
		int m = 0;
		for (int i = 1; i <= n; i ++) {
			int s, e, l;
			cin >> s >> e >> l;
			stone[i] = {s, e, l};
			m += s;
		}
		sort(stone + 1, stone + 1 + n);
		memset(f, -0x3f, sizeof f);
		f[0] = 0;
		for (int i = 1; i <= n; i ++) {
			int s = stone[i].s, e = stone[i].e, l = stone[i].l;
			for (int j = m; j >= s; j --)
				f[j] = max(f[j], f[j - s] + e - (j - s) * l);
		}
		int res = 0;
		for (int i = 0; i <= m; i ++)	res = max(res, f[i]);
		printf("Case #%d: %d\n", C, res);
	}
	return 0;
}

---

1. 贪心
   考虑前后吃的两块能量石 \(i\) 和 \(i + 1\)，\(E_i^{'}\) 和 \(E_{i + 1}^{'}\) 分别表示在准备吃 \(i\) 和 \(i + 1\) 时剩余的能量
   先吃 \(i\)，所获得的能量为 $E_i^{'} + E_{i + 1}^{'} - S_i \cdot L_{i + 1} $
   先吃 \(i + 1\)，所获得的能量为 $E_{i + 1}^{'} + E_{i}^{'} - S_{i + 1} \cdot L_{i} $
   要保证先吃 \(i\) 比先吃 \(i + 1\) 更优，即让 $E_i^{'} + E_{i + 1}^{'} - S_i \cdot L_{i + 1} > E_{i + 1}^{'} + E_{i}^{'} - S_{i + 1} \cdot L_{i} $，推出 $S_i \cdot L_{i + 1} < S_{i + 1} \cdot L_{i} $，也可以写为 \(\frac{S_i}{L_{i}} < \frac{S_{i + 1}}{L_{i + 1}}\)，那么按照 \(\frac{S_i}{L_{i}}\) 从小到大排序，从前往后选一定可以保证是最优的
2. 状态表示
   \(f[i][j]\) 表示从前 \(i\) 个物品中选，且总体积恰好是 \(j\) 的选法的最大值
3. 状态计算
   \(f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])\)
   这里的 \(v[i] = s[i]\)，\(w[i] = e[i] - (j - s[i]) * l[i]\)