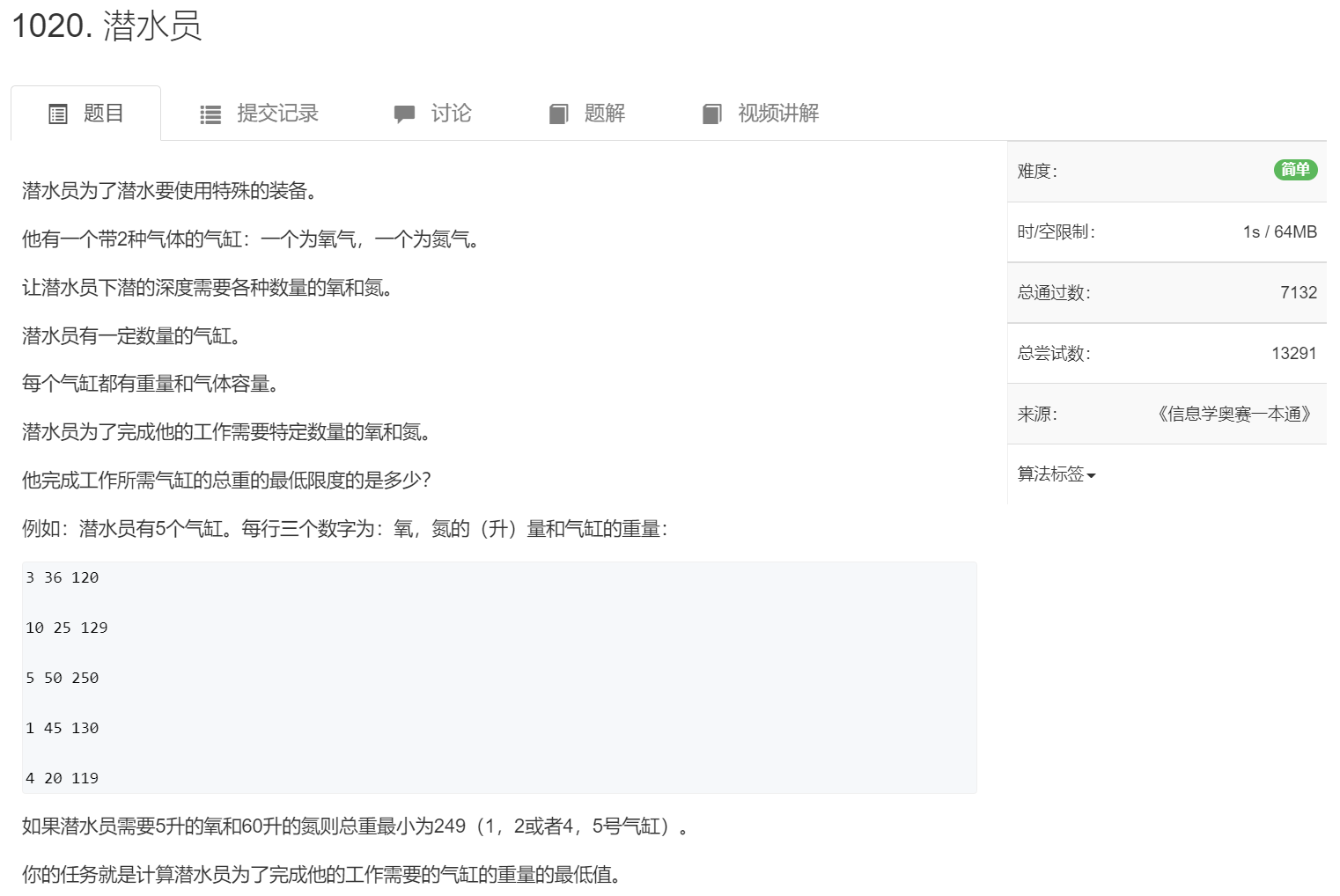
[AcWing 1020] 潜水员

---

点击查看代码

#include<iostream>
#include<cstring>
using namespace std;

const int N = 22, M = 80;

int n, m, t;
int f[N][M];

int main()
{
	cin >> n >> m >> t;
	memset(f, 0x3f, sizeof f);
	f[0][0] = 0;
	while (t --) {
		int v1, v2, w;
		cin >> v1 >> v2 >> w;
		for (int j = n; j >= 0; j --)
			for (int k = m; k >= 0; k --)
				f[j][k] = min(f[j][k], f[max(0, j - v1)][max(0, k - v2)] + w); 	
	} 
	cout << f[n][m] << endl;
	return 0;
}

---

1. 状态表示
   \(f[i][j][k]\) 表示从前 \(i\) 个物品中选，且体积 \(V_1\) 至少是 \(j\)，体积 \(V_2\) 至少是 \(k\) 的所有方案的最小值
2. 状态计算
   \(f[i][j][k] = min(f[i - 1][j][k], f[i - 1][j - v_1][k - v_2] + w)\)
   当 \(j - v_1 < 0\) 时，也是合法的方案，但是由于数组不能越界，取 \(max(0, j - v_1)\)
   当 \(k - v_2 < 0\) 时，也是合法的方案，但是由于数组不能越界，取 \(max(0, k - v_2)\)
   综上，\(f[i][j][k] = min(f[i - 1][j][k], f[i - 1][max(0, j - v_1)][max(0, k - v_2)] + w)\)