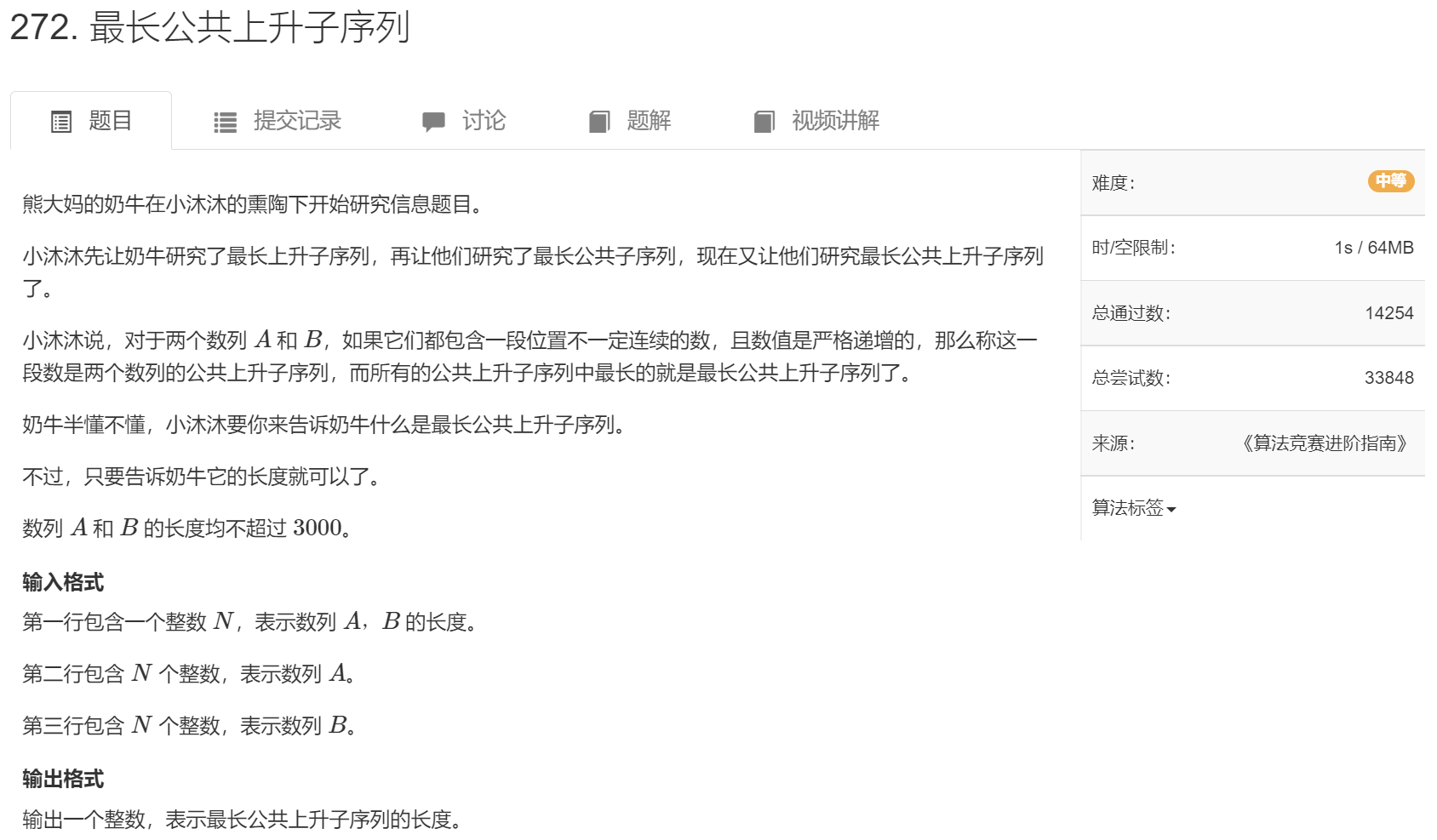
[AcWing 272] 最长公共上升子序列

---

点击查看代码

#include<iostream>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++)	cin >> a[i];
	for (int i = 1; i <= n; i ++)	cin >> b[i];
	for (int i = 1; i <= n; i ++) {
		int maxv = 1;
		for (int j = 1; j <= n; j ++) {
			f[i][j] = f[i - 1][j];
			if (a[i] == b[j])	f[i][j] = max(f[i][j], maxv);
			if (b[j] < a[i])	maxv = max(maxv, f[i - 1][j] + 1);
		}
	}
	int res = 0;
	for (int i = 1; i <= n; i ++)	res = max(res, f[n][i]);
	cout << res << endl;
	return 0;
}

---

1. 状态表示
   $f[i][j]$ 表示所有在 $a[1...i]$ 和 $b[1...j]$ 中都出现过，且以 $b[j]$ 为结尾的公共上升子序列的最大值
2. 状态计算
   ① $a[i]$ 不包含在公共上升子序列中，$f[i][j] = f[i - 1][j]$
   当 $a[i] = b[j]$ 时存在以下情况：
   ② 公共上升子序列的倒数第二个数不存在，$f[i][j] = 1$
   ③ 公共上升子序列的倒数第二个数是 $b[1]$，$f[i][j] = f[i - 1][1] + 1$
   $\cdots \cdots$
   ④ 公共上升子序列的倒数第二个数是 $b[j - 1]$，$f[i][j] = f[i - 1][j - 1] + 1$
3. 等价优化
   状态计算中，除 ① 外其他情况的前提为 $a[i] = b[j]$
   当 $a[i]$ 固定时，② 以后的更新依赖的是 $max(f[i - 1][1], f[i - 1][2], \cdots , f[i - 1][j - 1])$ ，而这个最大值 $maxv$ 可以记录下来，每次 $b[j] < a[i]$ 时，$maxv = max(maxv, f[i - 1][j] + 1)$ ($+1$ 是因为后续 $a[i] = b[j^{'}]$ 时才会用到 $maxv$)