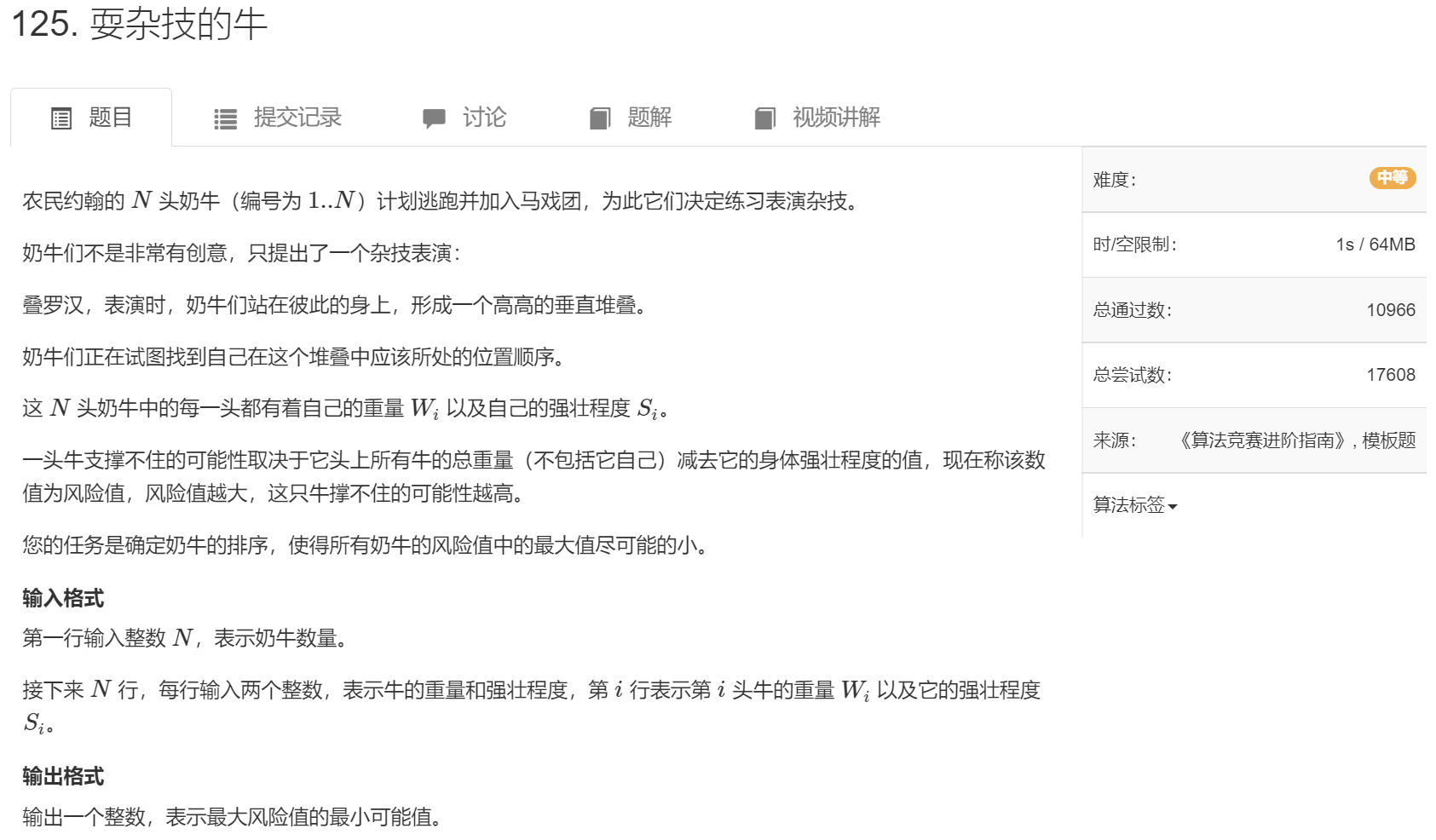
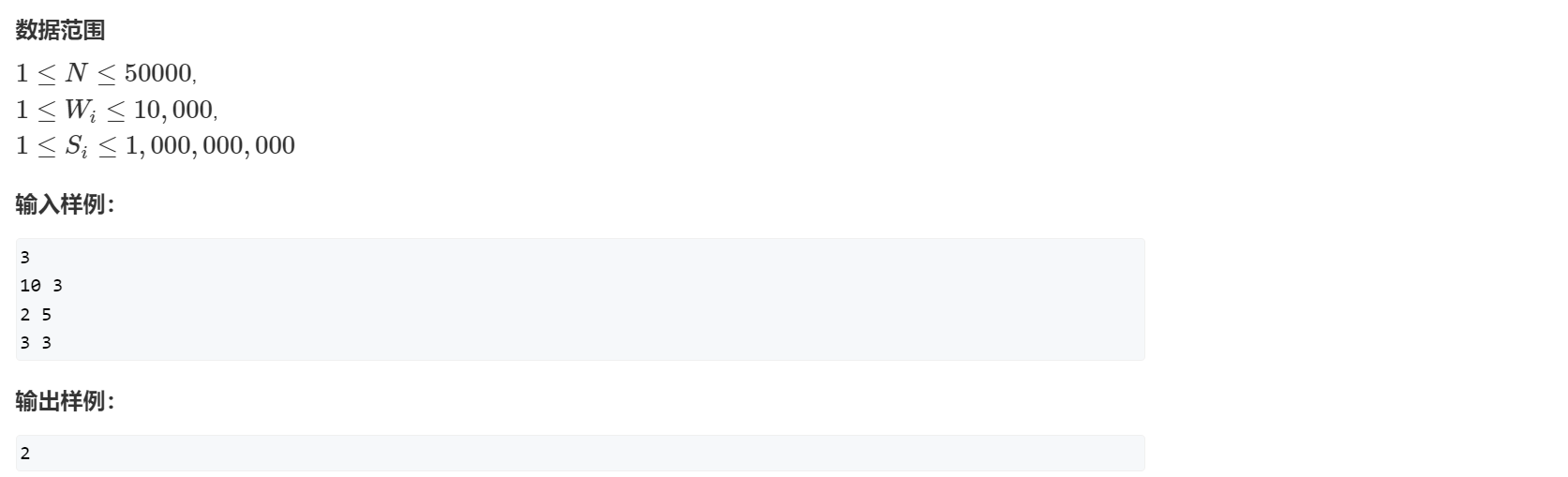
[AcWing 125] 耍杂技的牛

---

点击查看代码

 #include<iostream>
#include<algorithm>

using namespace std;

typedef pair<int,int> PII;

const int N = 1e5 + 10;

int n;
PII cow[N];

int main()
{
	cin >> n;
	for (int i = 0; i < n; i ++) {
		int w, s;
		cin >> w >> s; 
		cow[i] = {w + s, w};
	}
	sort(cow, cow + n);
	int res = -2e9, sum = 0;
	for (int i = 0; i < n; i ++) {
		int w = cow[i].second, s = cow[i].first - cow[i].second;
		res = max(res, sum - s);
		sum += w;
	}
	cout << res << endl;
	return 0;
}

---

1. 算法思路
   设 \(w_i\) 为第 \(i\) 头牛的重量，\(s_i\) 为第 \(i\) 头牛的强壮值
   按照 \(w_i + s_i\) 从小到大的顺序排，最大的风险值一定是最小的
2. 最优性证明
   调整法：假设存在 $w_i + s_i > w_{i+1} + s_{i+1} $ ，那么可得到第 \(i\) 个位置上的牛和第 \(i + 1\) 个位置上的牛的风险值 \(f\)
   ① 交换前
   第 \(i\) 个位置上的牛：$f_i = w_1 + w_2 + \cdots + w_{i-1} - s_{i} $
   第 \(i+1\) 个位置上的牛：$f_{i+1} = w_1 + w_2 + \cdots + w_{i} - s_{i+1} $
   ② 交换后
   第 \(i\) 个位置上的牛：$f_i^{'} = w_1 + w_2 + \cdots + w_{i-1} - s_{i+1} $
   第 \(i+1\) 个位置上的牛：$f_{i+1}^{'} = w_1 + w_2 + \cdots + w_{i+1} - s_{i} $
   比较 \(f_{i+1}\) 和 \(f_i^{'}\) 、 \(f_{i+1}^{'}\) ：
   $f_{i+1} - f_i^{'} = w_i > 0 $ ，即 \(f_{i+1} > f_i^{'}\) ，
   $f_{i+1} - f_{i+1}^{'} = (w_i+s_i)-(w_{i+1}+s_{i+1}) > 0 $ ，即 \(f_{i+1} > f_{i+1}^{'}\) ，
   可以推出 $max(f_i, f_{i+1}) \geqslant f_{i+1} > max(f_i^{'}, f_{i+1}^{'}) $
   交换后的结果一定是更优的，按照 \(w_i + s_i\) 从小到大的顺序排，最大的风险值一定是最小的