[AcWing 282] 石子合并

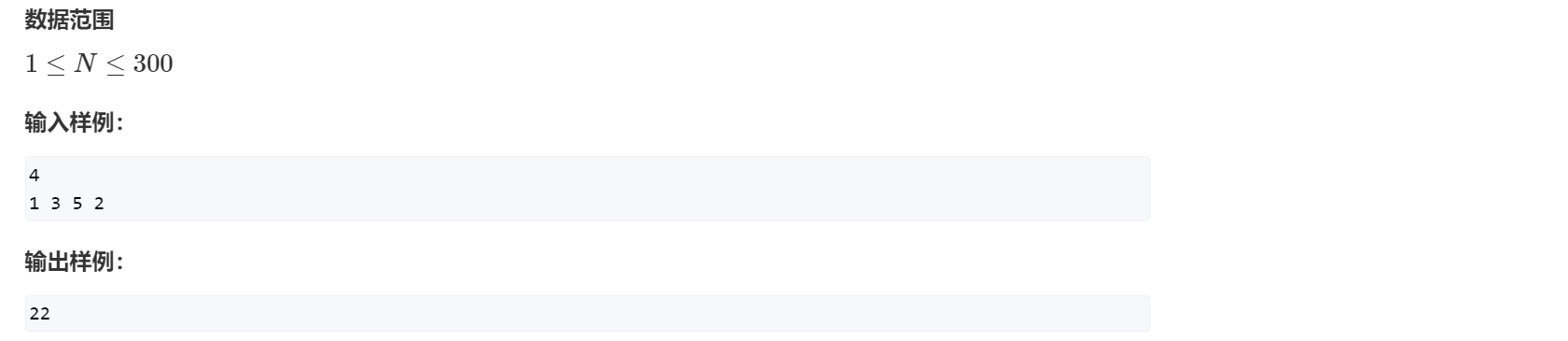
复杂度 $O(n^{3})$

总体复杂度 $300^{3} = 2.7 \times 10^{7}$

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 300 + 10;

int n;
int s[N];
int f[N][N];

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++)	cin >> s[i];
	for (int i = 1; i <= n; i ++)	s[i] += s[i - 1];
	for (int len = 2; len <= n; len ++)
		for (int i = 1; i + len - 1 <= n; i ++) {
			int l = i, r = i + len - 1;
			f[l][r] = 1e9;
			for (int k = l; k < r; k ++)
				f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
		}
	cout << f[1][n] << endl;
	return 0;
}

---

1. 状态表示
   $f[i][j]$ 表示所有将第 $i$ 堆石子到 $j$ 堆石子合并成一堆石子的合并方法的最小值
2. 状态计算
   在 $[i \ , \ j]$ 区间选一条分界线 $k$ ，把区间分成两半
   $f[i][j] = min(f[i][k] + f[k + 1][j] + s[j] - s[i - 1])$ ，其中 $k = i \ , i + 1 \ , \cdots \ , j - 1$ ($\ k < j$ 是因为要保证右半边至少有一堆石子)，$s[j] - s[i - 1]$ 是使用前缀和求得的 $[i, j]$ 石子的总重量