[AcWing 902] 最短编辑距离

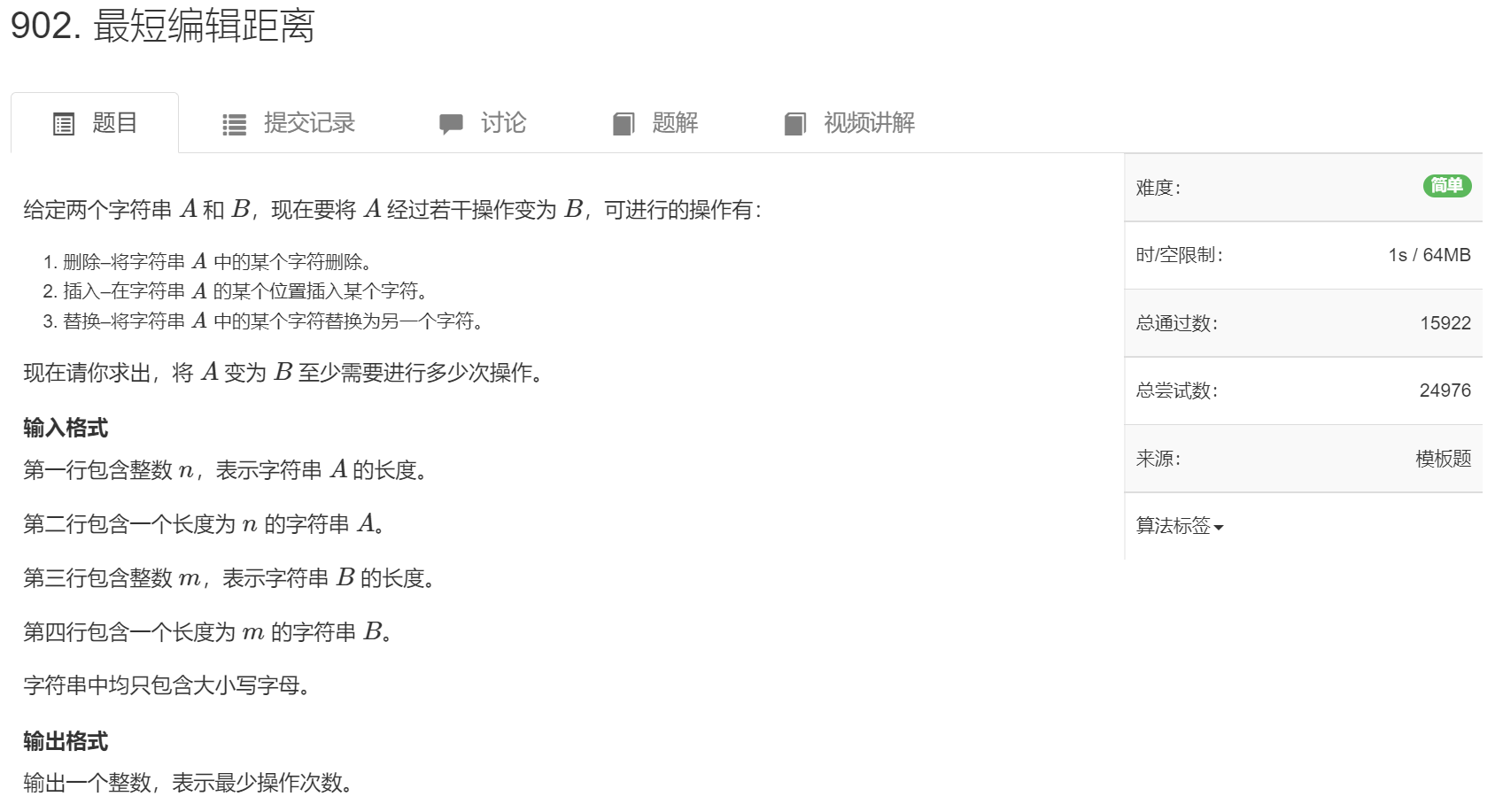
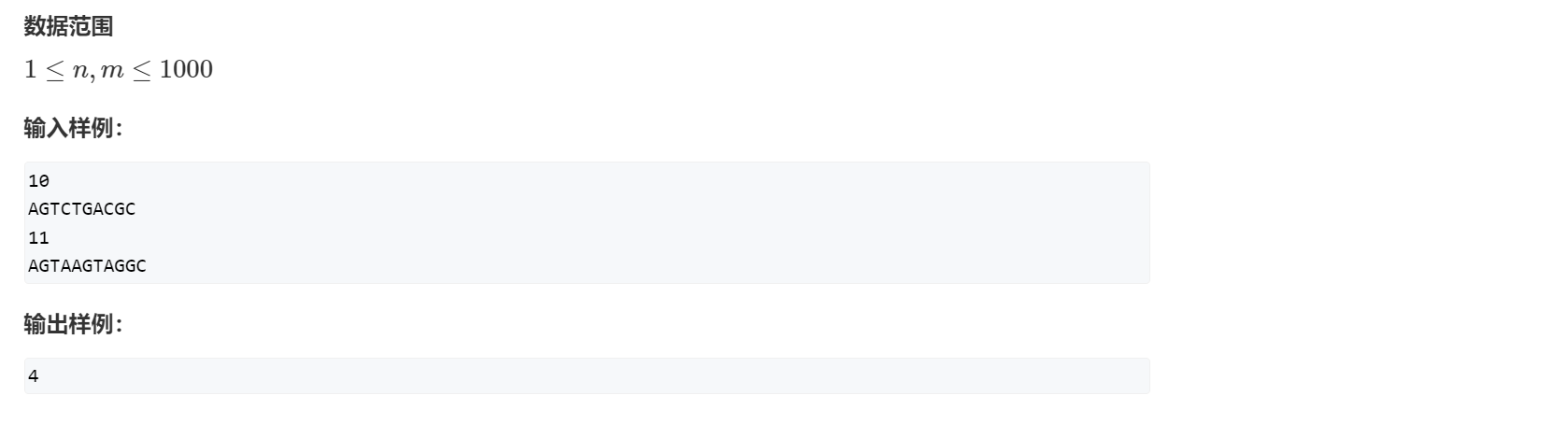
复杂度 $O(n^{2})$

总体复杂度 $1000^{2} = 1 \times 10^{6}$

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 1010; 
int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
	cin >> n >> a + 1;
	cin >> m >> b + 1;
	for (int i = 0; i <= m; i ++)	f[0][i] = i;
	for (int i = 0; i <= n; i ++)	f[i][0] = i;
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++) {
			f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
			if (a[i] == b[j])	f[i][j] = min(f[i][j], f[i - 1][j - 1]);
			else	f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
		}
	cout << f[n][m] << endl;
	return 0;
}

---

1. 状态表示
   $f[i][j]$ 表示将字符串 $a$ 的前 $i$ 个字母变成字符串 $b$ 的前 $j$ 个字母所需要的最小操作次数
2. 状态转移
   $f[i][j]$ 的更新分为三种情况：
   ① 字符串 $a$ 删除 $a[i]$ ，问题等价于将字符串 $a$ 的前 $i - 1$ 个字母变成字符串 $b$ 的前 $j$ 个字母所需要的最小操作次数再加上删除这一步操作，$f[i][j] = f[i - 1][j] + 1$
   ② 字符串 $a$ 后面插入 $b[j]$ ，问题等价于将字符串 $a$ 的前 $i$ 个字母变成字符串 $b$ 的前 $j - 1$ 个字母所需要的最小操作次数再加上插入这一步操作，$f[i][j] = f[i ][j - 1] + 1$
   ③ 将 $a[i]$ 替换为 $b[j]$ ，问题等价于将字符串 $a$ 的前 $i - 1$ 个字母变成字符串 $b$ 的前 $j - 1$ 个字母所需要的最小操作次数再加上替换这一步操作，当 $a[i] = b[j]$ 时，替换这一步是不需要的，所有要再细分为两种情况：
   如果 $a[i] = b[j]$ ，$f[i][j] = f[i - 1][j - 1]$
   如果 $a[i] \neq b[j]$ ，$f[i][j] = f[i - 1][j - 1] + 1$
3. 初始化
   ① $f[0][j]$ 表示将空字符串 $a$ 变成长度为 $j$ 的字符串 $b$ ，需要 $j$ 次插入操作
   ② $f[i][0]$ 表示将长度为 $i$ 的字符串 $a$ 变成空字符串 $b$ ，需要 $i$ 次删除操作