[AcWing 895] 最长上升子序列 Ⅰ Ⅱ

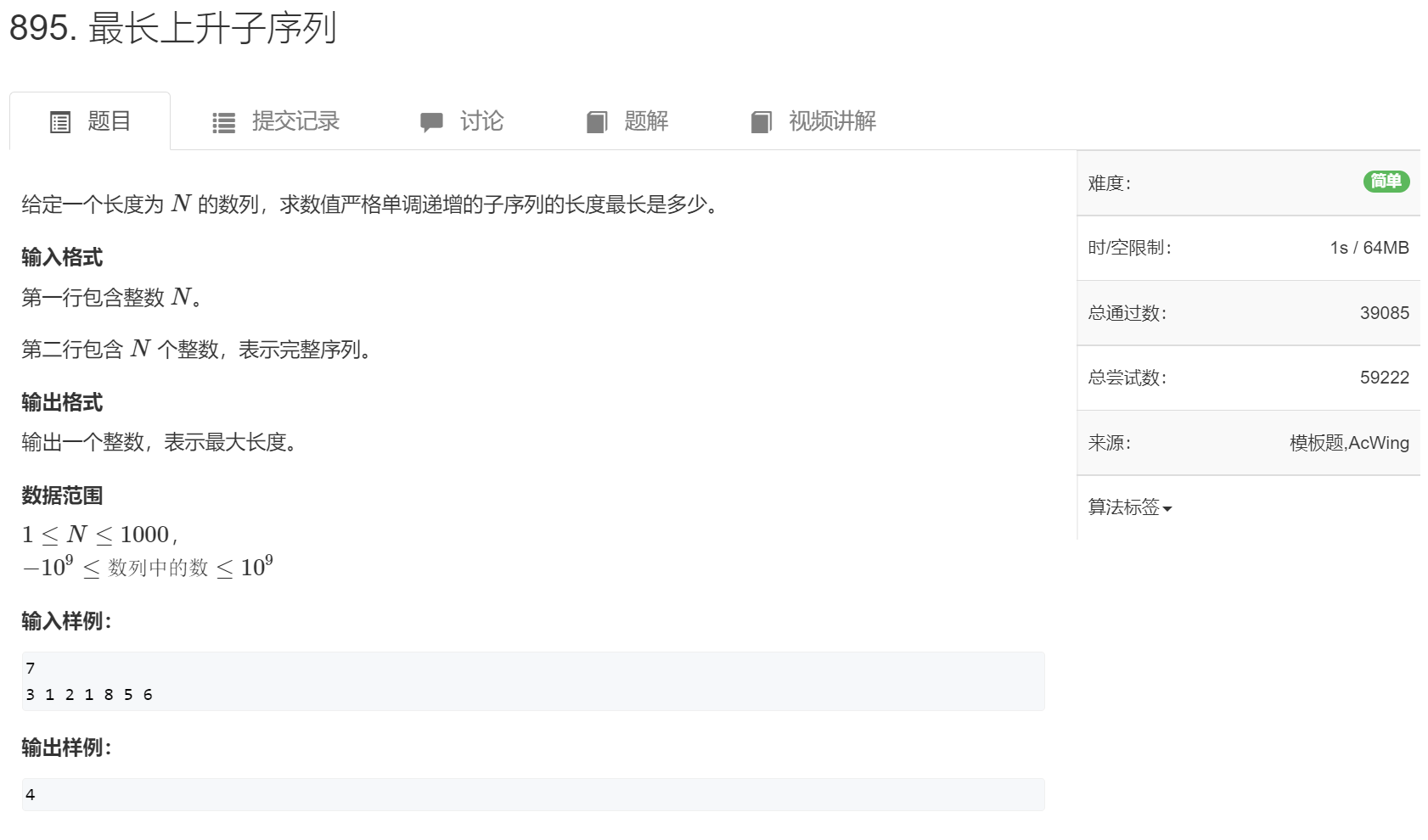
线性 dp 复杂度 $O(n^{2})$

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 1010;
int n;
int a[N], f[N];

int main()
{
	cin >> n;
	for (int i = 0; i < n; i ++)	cin >> a[i];
	for (int i = 0; i < n; i ++) {
	    f[i] = 1;
		for (int j = 0; j < i; j ++) {
			if (a[j] < a[i])
				f[i] = max(f[i], f[j] + 1);
		}
	}
	int res = 0;
	for (int i = 0; i < n; i ++)	res = max(res, f[i]);
	cout << res << endl;
	return 0;
}

---

1. 状态表示
   $f[i]$ 表示以 $a[i]$ 为结尾的上升子序列的长度
2. 状态转移
   $f[i] = max(f[j]) + 1$ ，其中 $j = 0, 1, 2, 3, \cdots, i - 1$ ，并且 $a[j] < a[i]$

---

贪心 + 二分 复杂度 $O(n \cdot log(n))$

---

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int n, m;
int a[N], f[N];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; i ++)
        cin >> a[i];
    int len = 0;
    for (int i = 1; i <= n; i ++) {
        int l = 0, r = len;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (f[mid] < a[i])
                l = mid;
            else
                r = mid - 1;
        }
        len = max(len, l + 1);
        f[l + 1] = a[i];
    }
    cout << len << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    solve();

    return 0;
}

---

1. $f[i]$ 用来记录长度为 $i$ 的子序列的最后一个元素的值，$f[i]$ 是单调递增的，证明如下：
   当有一个新的元素 $x$ 时，从后往前找到第一个小于 $x$ 的 $f[i]$，在 $f[i]$ 的序列后面接上 $x$，序列的长度变为 $i + 1$，而且满足最后一个元素的值 $x < f[i + 1]$，将 $f[i + 1]$ 更新为 $x$，可以保证 $f$ 是单调递增的