[AcWing 898] 数字三角形

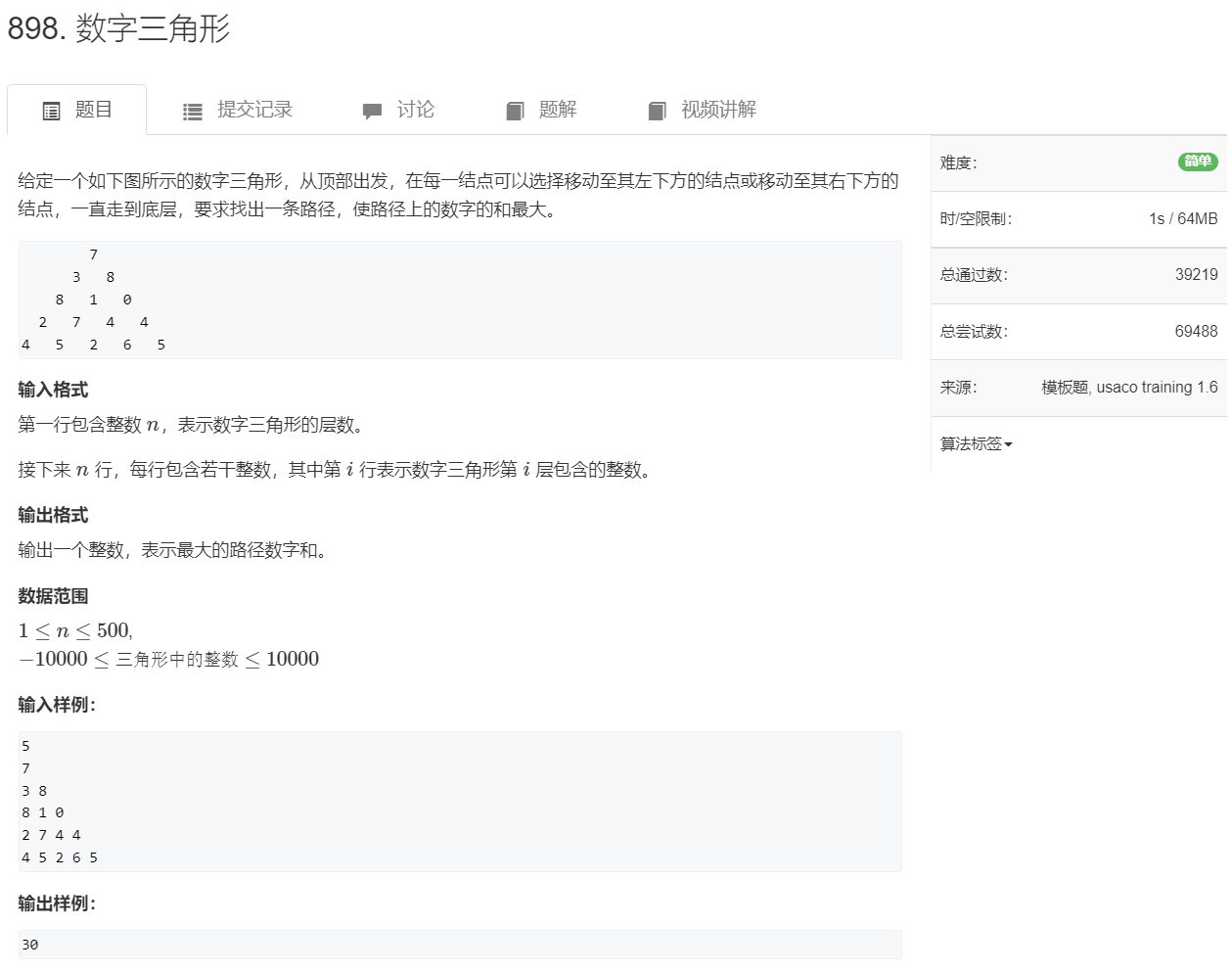
使用一维数组优化 复杂度 $n^{2}$

总体复杂度 $500^{2} = 2.5 \times 10^{5}$

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N], f[N];

int main()
{
    cin >> n;
    for (int i = 0; i <= n; i ++)
        f[i] = -INF;
    cin >> f[1];
    for (int i = 2; i <= n; i ++)
        for (int j = i; j >= 1; j --) {
            scanf("%d", &a[j]);
            f[j] = max(f[j], f[j - 1]) + a[j];
        }
    int res =  -INF;
    for (int i = 1; i <= n; i ++)   res = max(f[i], res);
    cout << res << endl;
    return 0;
}

---

1. 状态转移
   $f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]$ ，
   其中，$f[i][j]$ 表示从顶部出发，到第 $i$ 层的第 $j$ 个数的最大路径和，$a[i][j]$ 表示第 $i$ 层的第 $j$ 个数
2. 边界条件
   ① $f[i][j]$ 初始化为负无穷；
   ② 先读入 $f[1][1]$