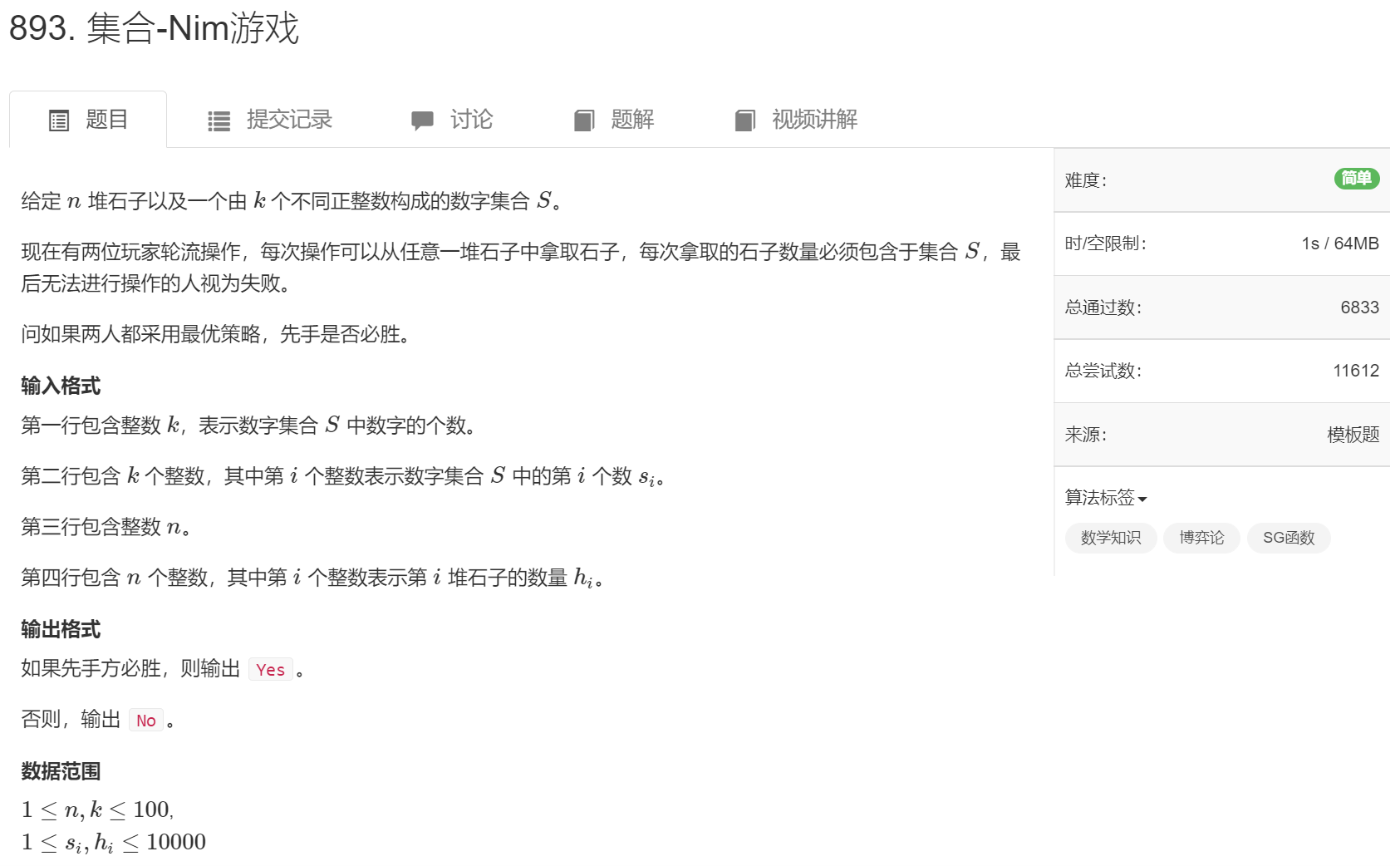
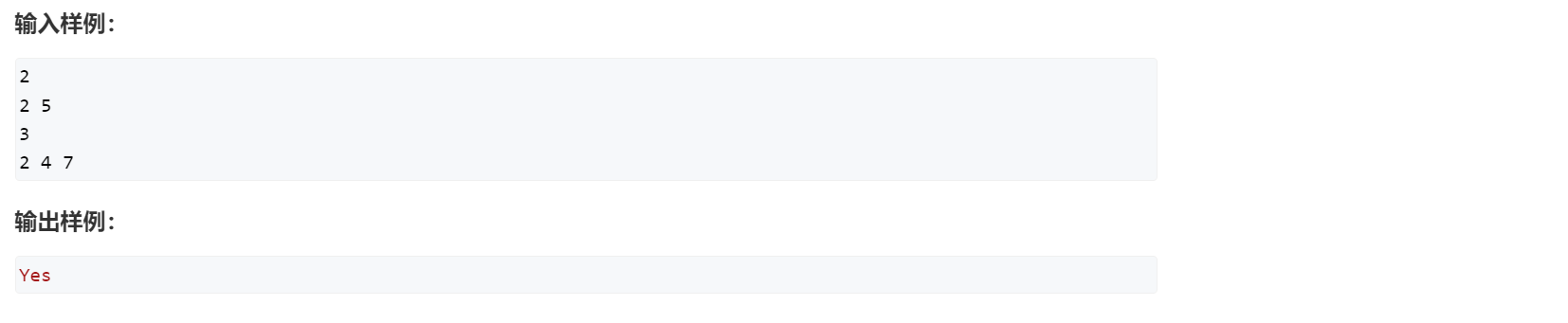
[AcWing 893] 集合-Nim游戏

---

点击查看代码

#include<iostream>
#include<cstring>
#include<unordered_set>

using namespace std;
const int N = 110, M = 1e4 + 10;
int k, n;
int s[N], f[M];
//s存储的是可供选择的集合,f存储的是所有可能出现过的情况的sg值

int sg(int x)
{
    if (f[x] != -1)     return f[x];
    //因为取石子数目的集合是已经确定了的,所以每个数的sg值也都是确定的,如果存储过了,直接返回即可
    unordered_set<int> S;
    //set代表的是有序集合(注:因为在函数内部定义,所以下一次递归中的S不与本次相同)
    for (int i = 0; i < k; i ++) {
        int sum = s[i];
        if (x >= sum)    S.insert(sg(x - sum));
        //先延伸到终点的sg值后,再从后往前排查出所有数的sg值
    }
    for (int i = 0; ; i ++)
        //循环完之后可以进行选出最小的没有出现的自然数的操作
        if (!S.count(i))
            return f[x] = i;
}
int main()
{
    cin >> k;
    for (int i = 0; i < k; i ++)    cin >> s[i];
    cin >> n;
    memset(f, -1, sizeof f);
    int res = 0;
    for (int i = 0; i < n; i ++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res)    puts("Yes");
    else    puts("No");
    return 0;
}

---

1. $ mex $ 运算
   定义 $ S $ 表示一个非负整数集合，定义 $ mex(S) $ 为：求出不属于 $ S $ 的最小非负整数；
2. $ SG $ 函数
   在有向图游戏中，对于每个节点 $ x $，设从 $ x $ 出发共有 $ k $ 条有向边，分别到达节点 $ y_1, y_2, \cdots, y_k $，则 $ SG(x) = mex( $ \(\{\) $ SG(y_1), SG(y_2), \cdots, SG(y_k) $ \(\}\) $ ) $ ，特别地，对于没有后继节点的节点 \(x\)，$ SG(x) = 0 $，整个有向图 $ G $ 的 $ SG $ 函数值被定义为有向图起点 $ s $ 的 $ SG $ 函数值，即 $ SG(G) = SG(s)$
3. 一个有向图的情况
   当只有一个有向图时，如果 $ SG(s) \neq 0 $ ，则先手必胜，否则，先手必败
   证明：如果 $ SG(s) \neq 0 $，说明从 $ s $ 可以走到 $ SG = 0 $ 的点，而根据 $ mex $ 函数的定义，$ SG = 0 $ 的点走到的点一定满足 $ SG > 0 $，如此一来，先手必然是走到最后一个根节点的那个人，而后手将无路可走；
4. 多个有向图的情况
   当有多个有向图时，如果 $ SG(s_1) \oplus SG(s_2) \oplus \cdots \oplus SG(s_n) = x \neq 0 $ ，则先手必胜，否则，先手必败
   证明：（和经典 Nim 游戏类似）
   ① 若 $ SG(s_1) = SG(s_2) = \cdots = SG(s_n) = 0 $，那么无论选哪个图，在单个图上都必败；
   ② 若 $ SG(s_1) \oplus SG(s_2) \oplus \cdots \oplus SG(s_n) = x \neq 0 $，一定存在 $ SG(s_i) $，使得 $ SG(s_i) \oplus x < SG(s_i) $，而根据 $ mex $ 函数的定义，$ SG(s_i) $ 一定可以走到 $ SG(s_i) \oplus x $ 这个节点，这时 $ SG(s_1) \oplus SG(s_2) \oplus \cdots \oplus SG(s_n) = x \oplus x = 0 $
   ③ 若 $ SG(s_1) \oplus SG(s_2) \oplus \cdots \oplus SG(s_n) = 0 $，那么无论怎么走，下一次的异或值必不为 $ 0 $
   反证法：如果要让下一次的异或值为 $ 0 $，那么 $ SG(s_i) = k $ 一定要走到 $ SG = k $ 的点，而这与 $ mex $ 函数的定义矛盾，故下一次的异或值必不为 $ 0 $