[AcWing 889] 满足条件的01序列

---

点击查看代码

#include<iostream>

using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;

int qmi(int a, int k)
{
    int res =  1;
    while (k) {
        if (k & 1)  res = (LL) res * a % mod;
        k >>= 1;
        a = (LL) a * a % mod;
    }
    return res;
}
int main()
{
    int n, res = 1;
    cin >> n;
    int a = 2 * n, b = n;
    for (int i = a; i > a - b; i --)    res = (LL) res * i % mod;
    for (int i = 1; i <= b; i ++)   res = (LL) res * qmi(i, mod - 2) % mod;
    res = (LL) res * qmi(n + 1, mod - 2) % mod;
    cout << res;
    return 0;
}

---

1. 卡特兰数的公式为 $ \frac{C_{2n}^{n}}{n + 1} $
   
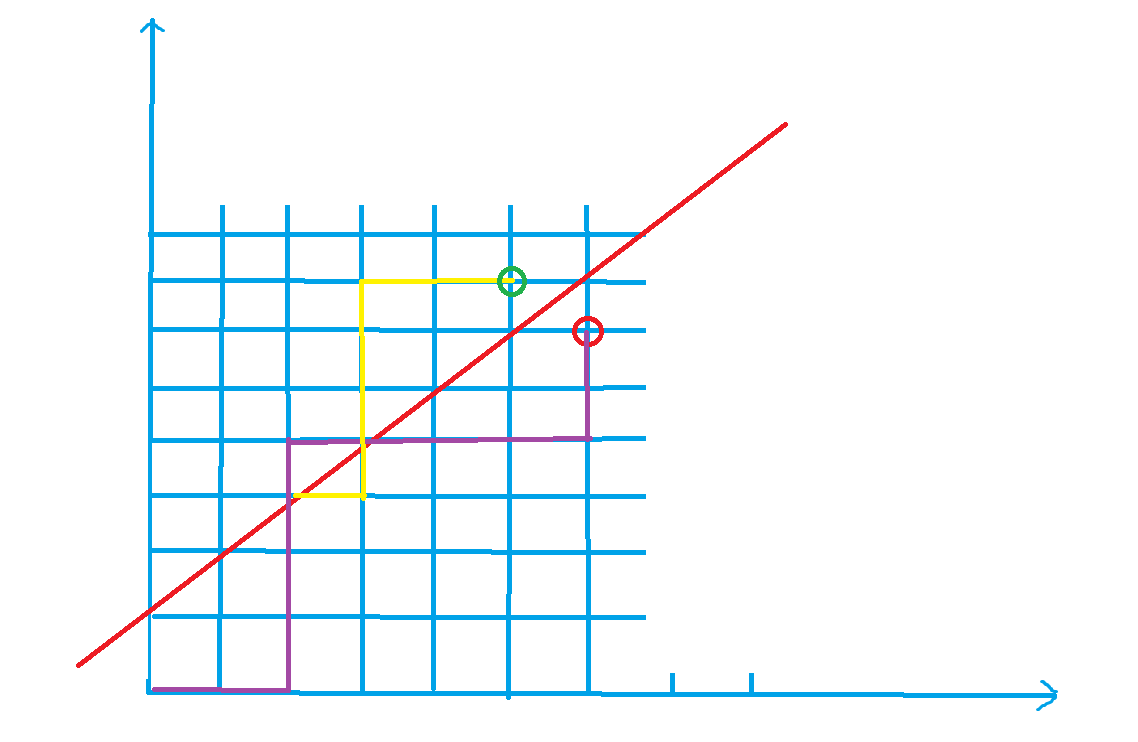
   n 取 6 时，题目的问题等价于：从原点走到点 (6, 6) ，始终在红线下方的路径的个数，原因：任意前缀中 0 的个数都不少于 1 的个数，对应到坐标上，可以看作是在路径上的任意点 x >= y，在图中，当路径上的点都在红线以下时，满足要求；
   由对称性，任意一条不合法的路径都可以通过对称，将路径和红色直线第一个交点后面的部分关于红色直线对称，都能达到 (5, 7) 这个点，而由于原点和(5,7)分别位于红色直线的两侧，能到达 (5, 7) 的路线必定会经过红线，由此可知，不符合要求的路线数即为原点到 (5, 7) 的路径个数，即为 $ C_{12}^{5} $ ，而从原点到 (6,6) 的总路径个数为 $ C_{12}^{6} $ ，故满足要求的路径个数为 $ C_{12}^{6} - C_{12}^{5} $
   推广到更一般的情况，对于任意一点 (n, n)，满足要求的路径个数为 $ C_{2n}^{n} - C_{2n}^{n-1} = \frac{(2n)!}{n! \ n!} - \frac{(2n)!}{(n - 1)! \ (n + 1)!} = \frac{(2n!)(n + 1 - n)}{n! \ (n + 1)!} = \frac{1}{n+1} \frac{(2n)!}{n! \ n!} = \frac{C_{2n}^{n}}{n + 1} $ ，最后得到的结果即为卡特兰数；
2. 常见的卡特兰数问题
   ① n 个元素进栈序列为：1，2，3，4，...，n，则有多少种出栈序列。
   ② n 对括号，则有多少种 “括号匹配” 的括号序列
   ③ n + 1 个叶子节点能够构成多少种形状不同的满二叉树