[AcWing 875] 快速幂

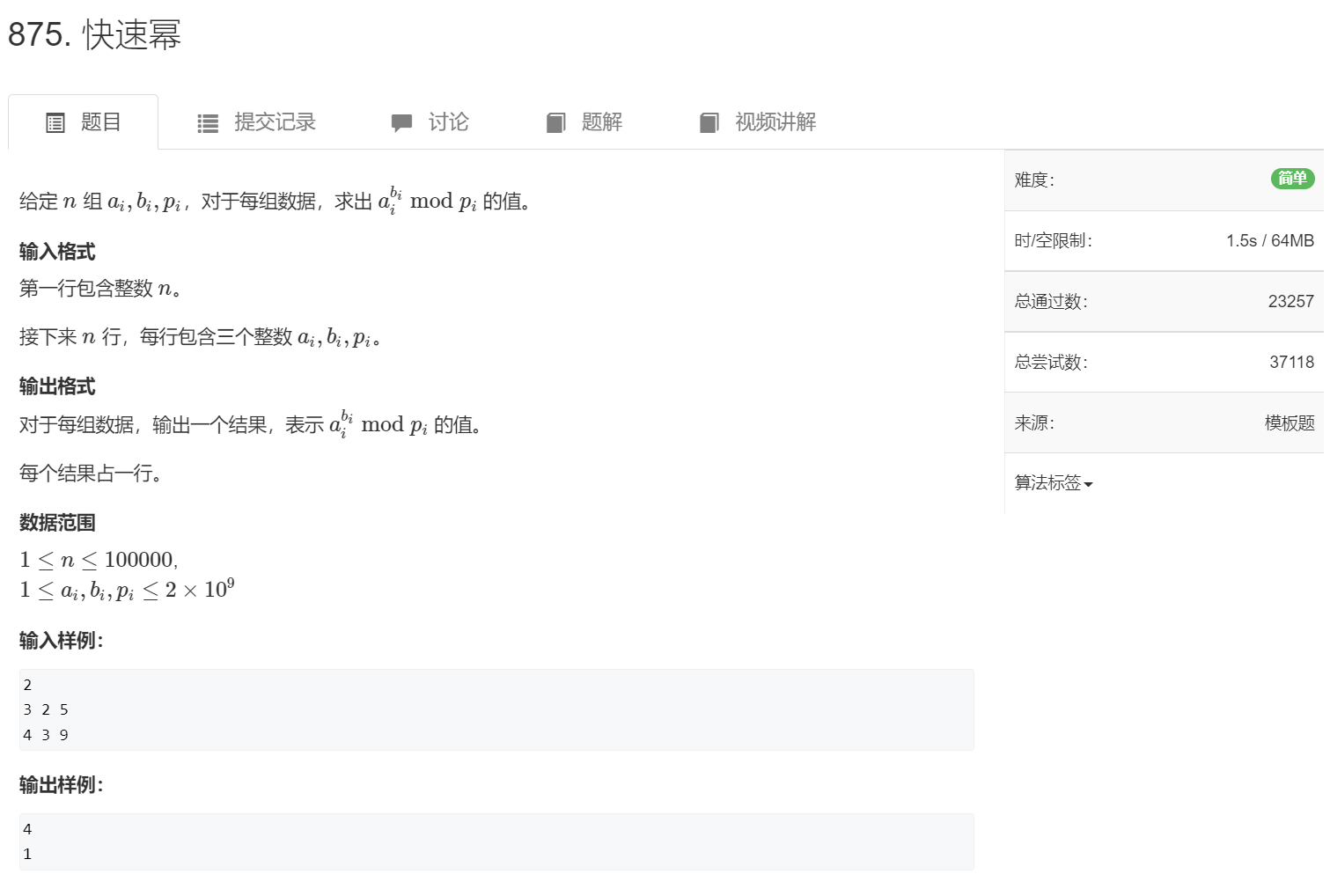
复杂度 $O(log(k))$ （k 是指数）

总体复杂度 $10^{5} \times log(2 \times 10^{9}) \approx 4 \times 10^{6}$

---

点击查看代码

#include<iostream>

using namespace std;
typedef long long LL;

LL qmi(int a, int k, int p)
{
    LL res = 1;
    while (k) {
        if (k & 1)  res = res * a % p;
        k >>= 1;
        a = (LL) a * a % p;
    }
    return res;
}
int main()
{
    int n;
    scanf("%d", &n);
    while (n --) {
        int a, b, p;
        scanf("%d %d %d", &a, &b, &p);
        printf("%lld\n", qmi(a, b, p));
    }
    return 0;
}

---

1. 快速幂的思路：
   ① $b = c_1 \cdot2^{0} + c_2 \cdot 2^{1} + \cdots + c_k \cdot 2^{k}$
   $a^{b} = a^{ c_1 \cdot2^{0} + c_2 \cdot 2^{1} + \cdots + c_k \cdot 2^{k} } = a^{ c_1 \cdot2^{0} } \cdot a^{ c_2 \cdot 2^{1} } \cdots a^{ c_k \cdot 2^{k} }$
   ② 由 ① ，只需找到 $c_i = 1$ 对应的乘积项，下标记为 $i$ ~ $j$ $a^{b} \bmod p = ( \cdots (( a^{ c_i \cdot 2^{i} } \bmod p) \cdot a^{ c_{ i + 1 } \cdot 2^{i + 1} } \bmod p) \cdots) \cdot a^{ c_j \cdot 2^{j} } \bmod p$
2. 实现方式：
   每次让 $b$ & 1 取出最低位，判断是否为 1，若是 1，就把这一位对应的乘积项代入上述公式计算，每次都让 $b$ 右移一位，并把 $a \times a \bmod p$ （强制类型转换为 long long，防止爆 int）