[AcWing 873] 欧拉函数

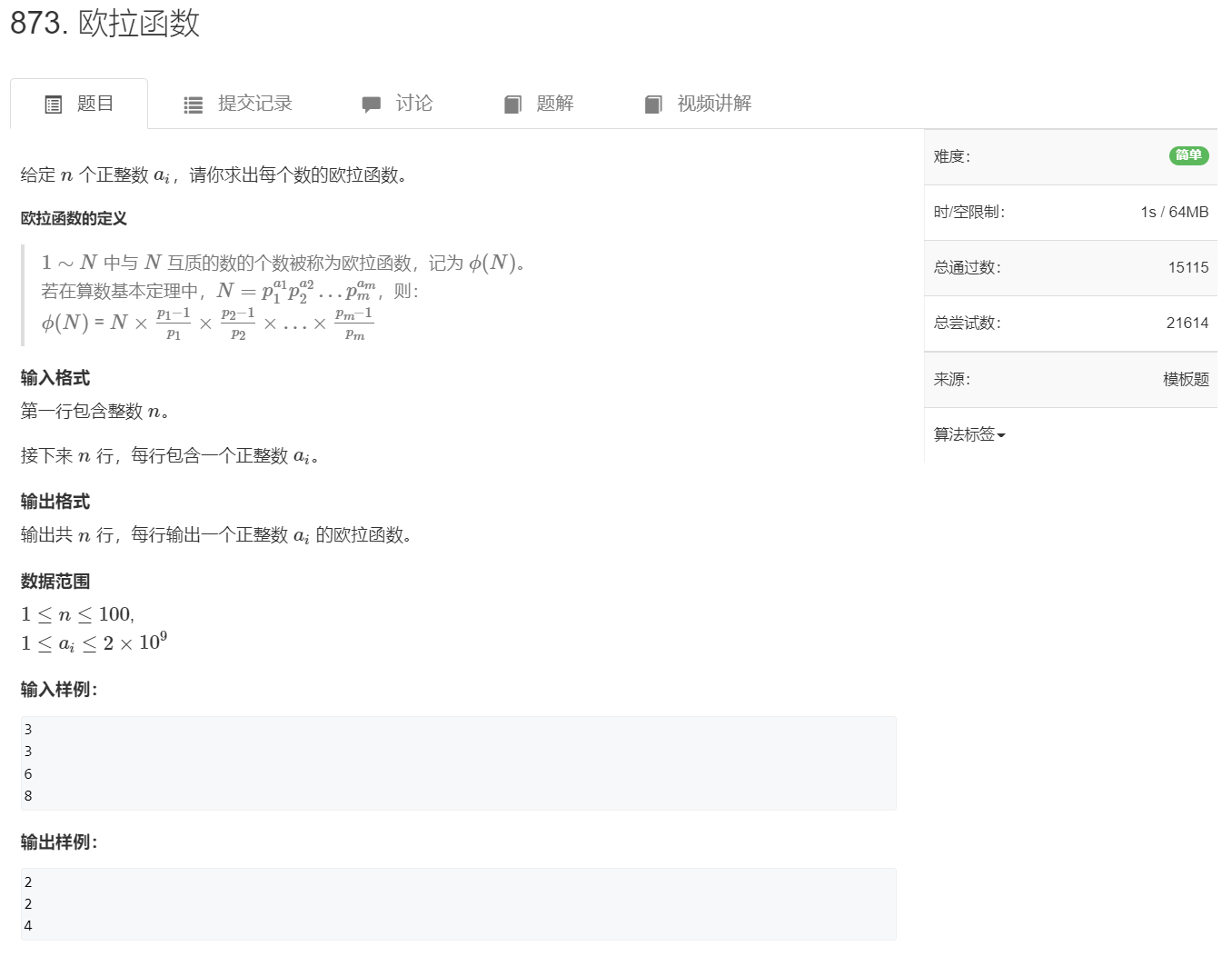
复杂度 $ O(\sqrt{n}) $

总体复杂度 $ 100 \times \sqrt{2 \times 10^{9}} \approx 4.5 \times 10^{6} $

---

点击查看代码

#include<iostream>

using namespace std;

void solve(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++) {
        if (x % i == 0) {
            res = res / i * (i - 1);
            while (x % i == 0)  x /= i;
        }
    }
    if (x > 1)      res = res / x * (x - 1);
    cout << res << endl;
}
int main()
{
    int n;
    cin >> n;
    while (n --) {
        int x;
        cin >> x;
        solve(x);
    }
    return 0;
}

---

1. 欧拉函数的定义
   $ 1 $ ~ $ N $ 中与 $ N $ 互质的数的个数被称为欧拉函数，记为 $ \phi (N) $ ，
   若在算数基本定理中，$ N = p_1^{\alpha_1} p_2^{\alpha_2} \cdots p_m ^ {\alpha_m} $ ，则
   $ \phi (N) = N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times \cdots \times \frac{p_m-1}{p_m} $
2. 欧拉函数公式的证明
   $ \phi (N) = N \times \frac{p_1-1}{p_1} \times \frac{p_2-1}{p_2} \times \cdots \times \frac{p_m-1}{p_m} = N \times (1 - \frac{1}{p_1} ) \times (1 - \frac{1}{p_2}) \times \cdots \times (1 - \frac{1}{p_m}) $ ，
   $ 1 $ ~ $ N $ 中与 $ N $ 互质的数的个数等于 $ N $ 减去 $ p_1 , \ p_2, \cdots , \ p_m $ 倍数的个数，剩下的数就都是和 $ N $ 互质的数，由容斥原理，可以得到：
   $ \phi (N) = N - \frac{N}{p_1} - \frac{N}{p_2}- \cdots + \frac{N}{p_1 \cdot p_2} + \frac{N}{p_1 \cdot p_3} + \cdots - \frac{N}{p_1 \cdot p_2 \cdot p_3} - \frac{N}{p_1 \cdot p_2 \cdot p_4} - \cdots + \frac{N}{p_1 \cdot p_2 \cdot p_3 \cdot p_4} + \cdots \cdots $
   将 $ \phi (N) = N \times (1 - \frac{1}{p_1} ) \times (1 - \frac{1}{p_2}) \times \cdots \times (1 - \frac{1}{p_m}) $ 展开，可以得到上式结果，说明两式子等价，证明完毕；
3. 在用公式计算时，要先进行除法，再进行乘法，也就是 res = res / i * ( i - 1 )，如果先进行乘法，会爆 int；（先除后乘肯定不会溢出）