[AcWing 849] Dijkstra求最短路 I

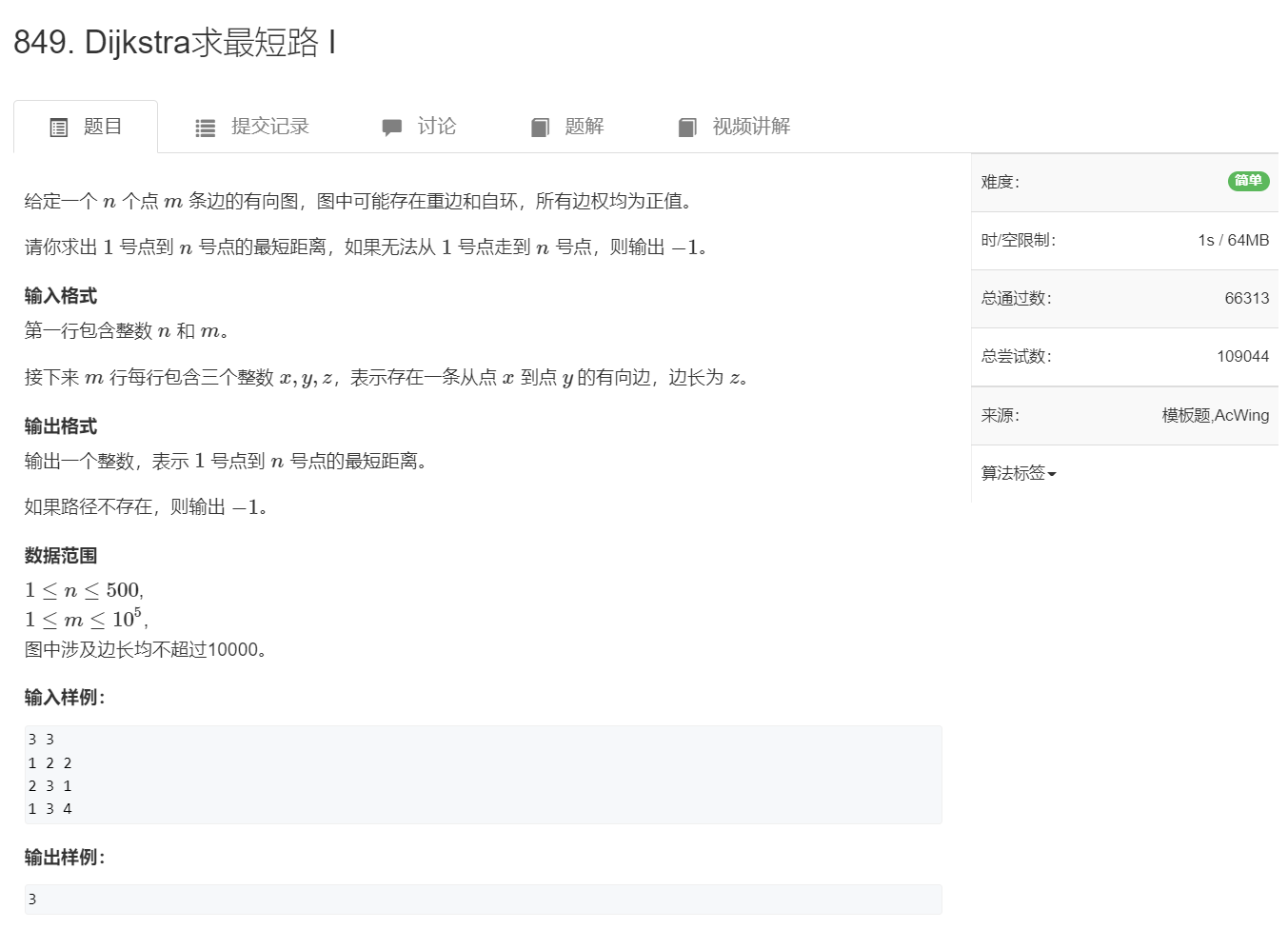
复杂度 $O(n^{2})$

---

点击查看代码

#include<iostream>
#include<cstring>

using namespace std;
const int N = 510;
int n, m;
int g[N][N], dist[N];
bool st[N];
int dijkstra()
{
    memset(dist, 0x3f, sizeof(dist));
    dist[1] = 0;
    for (int i = 0; i < n; i ++) {
        int t = -1;
        for (int j = 1; j <= n; j ++) {
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        }
        for (int i = 1; i <= n; i ++) {
            dist[i] = min(dist[i], dist[t] + g[t][i]);
        }
        st[t] = true;
    }
    if (dist[n] == 0x3f3f3f3f) return -1;
    else    return dist[n];
}
int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof(g));
    while (m --) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    cout << dijkstra() << endl;
    return 0;
}

---

1. 处理重边和自环的方法：对于重边，只保留权值最小的边，对于自环，不需要处理；（权值是正值，自环肯定不是最短路）
2. 朴素 dijkstra 模板；
3. 最外层循环 i < n -1 也可，因为在 i = n - 1 时，会将 dist[ n ] 更新为最小值；（n 还没有被访问）